Acerca del Rombo
About Rhombus
Ingrid Judith Orozco Martínez
Licenciada en Ciencias de la Educación con Mención en Matemática, Estudiante de Doctorado en Matemática Aplicada. UNAN-Maangua FAREM-Matagalpa
https://orcid.org/0000-0002-1362-3579
judithorozco655@gmail.com
Iván Augusto Cisneros Díaz
Doctor en Matemática Aplicada, UNAN-Managua, Nicaragua
https://orcid.org/0000-0003-2014-1946
ivan.cisneros@unan.edu.ni
Recibido
05/05/2022
Aceptado
12/07/2022
RESUMEN
Este trabajo aborda la interrelación conceptual y analíticas que se manifiestan y que son predominante entre los contenidos de la trigonometría plana y la geometría euclidiana, los cuales se desarrollan en los cursos regulares de la educación secundaria en nuestro país, además de estar sujeto al contenido programático de los programas analíticos del Ministerio de Educación (MINED). El trabajo presenta diversas variantes de la demostración matemática de las fórmulas del cálculo de área, operaciones con diagonales y lados del rombo, todas ellas obtenida mediante la combinación de técnicas demostrativas trigonométricas y de la geometría euclidiana. El objetivo cardinal es fundamentar de forma teórica y analítica el desarrollo de estos teoremas y, por otro lado, simularlo mediante programación de alto nivel mediante el lenguaje de programación Python. Cabe resaltar que los procesos demostrativos incluyen métodos y procedimientos lógicos que permiten nuevas formas de desarrollo matemáticos en las construcciones demostrativas. Se presentan otras estrategias de demostración, de manera que su construcción resulte apropiada para que el docente del nivel educativo de secundaria las pueda aplicar y que los docentes universitarios puedan profundizar más en dichas demostraciones y en sus diversas variantes. La combinación de técnicas demostrativas basada en las características analíticas y teóricas de la trigonometría con la geometría euclidiana, permitirá un mayor nivel en el desarrollo del carácter demostrativos de la matemática a este nivel. Se utiliza el método constructivo para desarrollar todas las demostraciones acerca del rombo y los enfoques deductivo e inductivo para poder generalizar dichos resultados.
PALABRAS CLAVES
Área; geometría; método constructivo; trigonometría; rombo
ABSTRACT
This work shows the conceptual and analytical interrelationship between the contents of plane trigonometry and Euclidean geometry, which are developed in the regular courses of secondary education in our country, besides being subject to the programmatic content of the analytical programs of the Ministry of Education (MINED). The work presents several variants of the mathematical demonstration of the area calculation formulas, operations with diagonals and sides of the rhombus, all of them obtained through the combination of trigonometric demonstrative techniques and Euclidean geometry. The cardinal objective is to provide a theoretical and analytical basis for the development of these theorems and, on the other hand, to simulate them by means of high-level programming using the Python programming language. It should be emphasized that the demonstrative processes include logical methods and procedures that allow new forms of mathematical development in the demonstrative constructions. Other demonstration strategies are presented, so that their construction is appropriate for the secondary school teacher to apply and for university teachers to go deeper into these demonstrations and their different variants. The combination of demonstrative techniques based on the analytical and theoretical characteristics of trigonometry with Euclidean geometry, will allow a higher level in the development of the demonstrative character of mathematics at this level. The constructive method is used to develop all the demonstrations about the rhombus and the deductive and inductive approaches to be able to generalize such results.
KEYWORDS
Area; geometry; constructive method; trigonometry; rhombus.
INTRODUCCIÓN
Uno de los principales problemas estudiado dentro del desarrollo metodológico de la matemática, es la construcción de las demostraciones matemáticas. Existen muchos problemas prácticos que requieren su solución mediante la aplicabilidad y combinatoria de la teoría trigonométrica y geométrica.
Los teoremas presentados en este artículo están referidos a la combinación de ambas disciplinas matemáticas, el uso correcto de estos teoremas constituye un fundamento teórico de la ciencia matemática. Se considera importante señalar que la justificación teórica de sus demostraciones es aún más importante, ya que permite ampliar el horizonte lógico y abstracto de la matemática (Orozco, 2022).
Desde un punto de vista teórico como práctico de las matemáticas aplicadas, muchas ramas de las ciencias, la ingeniería, la física, la geometría, el diseño de estructura, la informática, la astronomía, la inteligencia artificial y la robótica, etc. ponen de manifiesto un alto nivel de interés teórico en el desarrollo de la matemática y especialmente en las demostraciones de dichas fórmulas (Orozco, 2022)
Entre los principales valores metodológicos de este artículo, se pueden mencionar (Orozco, 2022)
- Diseño de nuevas estrategias de demostraciones matemáticas, mediante la conjugación o combinación de las teorías trigonométrica y geométrica.
- Aplicación de diferentes técnicas o procesos lógicos para una correcta demostración matemática.
- Evidenciar la importancia de la búsqueda de nuevos enfoques de paradigmas demostrativos.
MATERIALES Y MÉTODOS
En este apartado se desarrollan las diferentes variantes demostrativas de las fórmulas de áreas, fórmulas de las longitudes de las diagonales mayores y menores, fórmulas de operaciones con las diagonales y finalmente fórmulas de la longitud del lado del rombo. La metodología empleada es la construcción de las demostraciones matemáticas, mediante la combinación de la aplicabilidad de la teoría trigonométrica y de la geometría euclidiana.
La metodología empleada en este trabajo siguió las siguientes etapas (Orozco, 2022):
- Revisión bibliográfica sobre los procesos demostrativos de las fórmulas de áreas de figuras geométricas.
- Estudio de diversos procedimientos matemáticos mediante la combinación de la trigonometría y geometría.
- Formulación de nuevos procesos demostrativos por medios trigonométricos y geométricos.
- Implementación de los diferentes códigos en el Lenguaje de Programación Python, donde se simula diferentes fórmulas del cálculo de área, diagonales mayor y menor y longitud del lado del rombo.
RESULTADOS
FÓRMULAS DEL ÁREA DEL ROMBO
Teorema 1: El área del rombo está dado por
donde D y d es la diagonal mayor y menor respectivamente del rombo. (Barnet, 1991)
Demostración 1:
De acuerdo a la figura
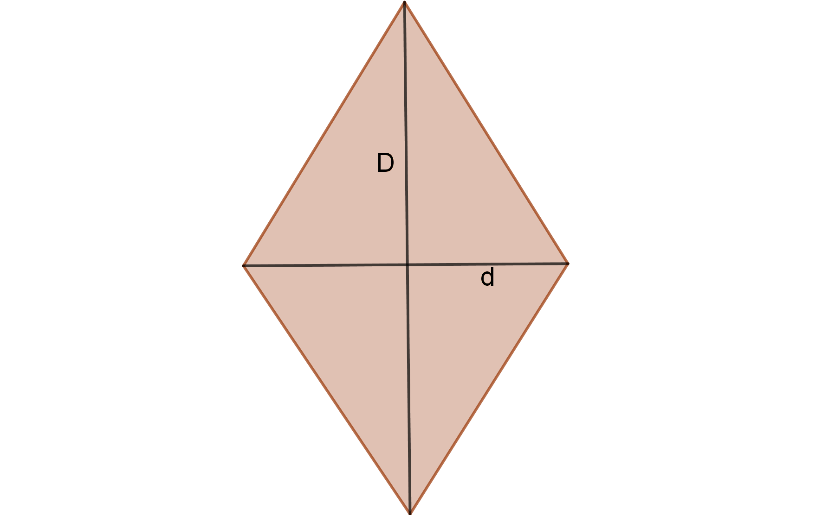
se forma un triángulo con base d/2 y altura D/2; ya que las diagonales en un rombo, se cortan en su punto medio, (Barnet, 1991) luego por la fórmula del área de un triángulo (Barnet, 1991) , se tiene
Demostración 2:
De acuerdo a la siguiente figura, podemos formar 2 triangulo de base D y altura d/2 , los cuales representan la longitud de la diagonal mayor y diagonal menor respectivamente. (Barnet, 1991)
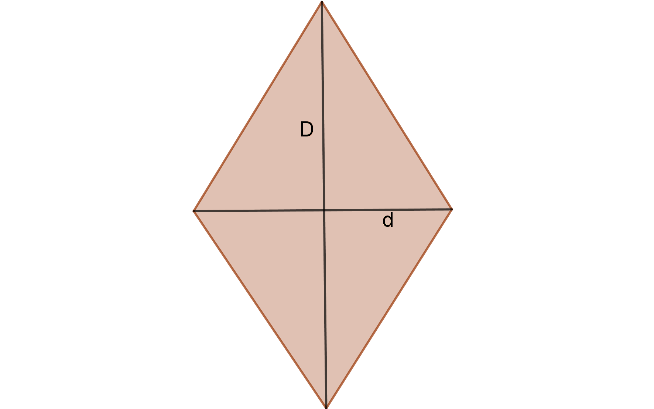
De acuerdo a la fórmula del área de un triángulo, se tiene que la altura es d/2 y la base es D; luego el área de un triángulo es
Teorema 2: El área de un rombo está dado por
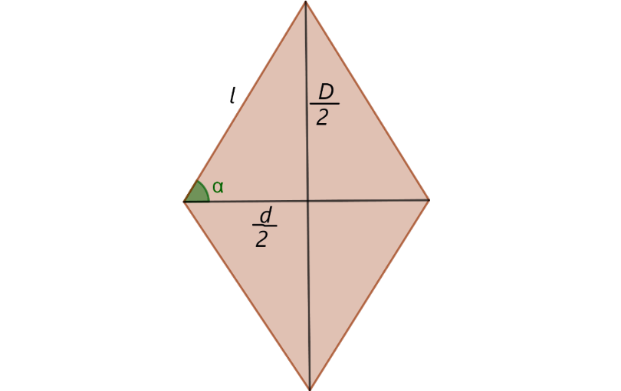
Donde l es el lado del rombo y α es la bisectriz (Barnet, 1991) de la diagonal menor.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
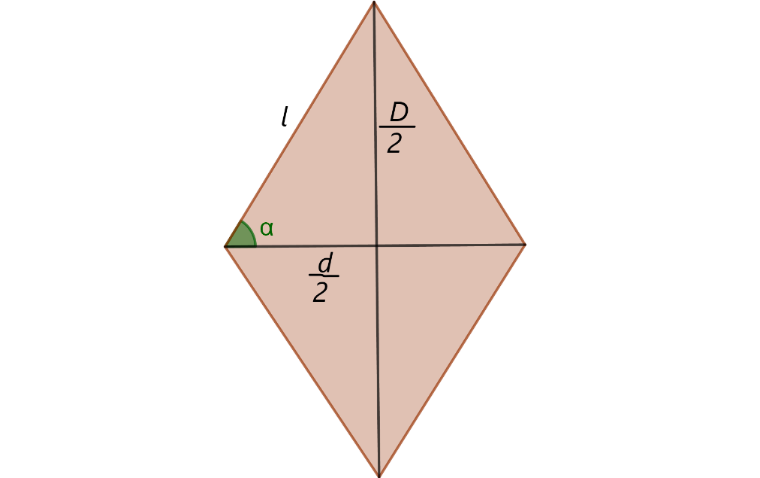
aplicando la definición de seno y coseno (Zill, 2012), respectivamente, se tiene
De manera similar
utilizando la fórmula del área de un rombo (Barnet, 1991), se tiene
luego
Teorema 3: El área de un rombo está dado por
donde d es la diagonal menor y α es el ángulo bisectriz de la diagonal menor.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
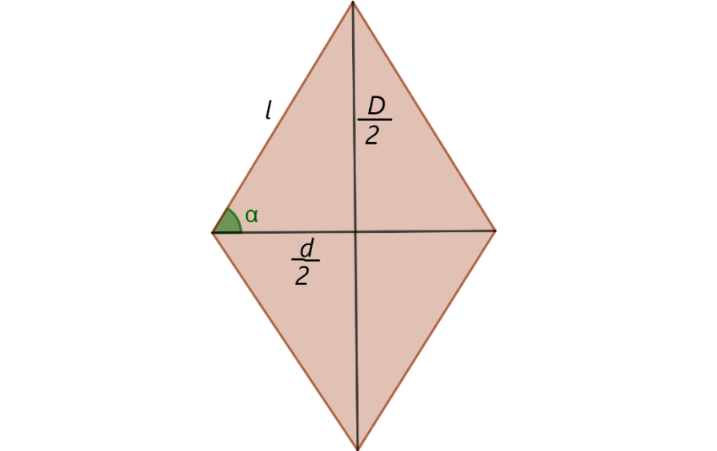
aplicando la definición de la función tangente (Zill, 2012)
luego, sustituyendo en la fórmula del área de un rombo (Barnet, 1991), se tiene
Teorema 4: El área de un rombo está dado por
donde D es la diagonal mayor y α es el ángulo bisectriz de la diagonal menor.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
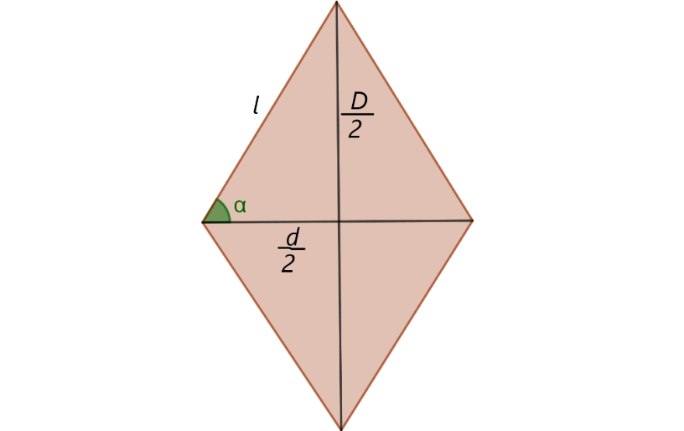
aplicando la definición de la función cotangente (Swokowski, 2009)
Luego, aplicando la fórmula del área de un rombo (Barnet, 1991), se tiene
Teorema 5: La diagonal mayor de un rombo está dado por
donde l y α son el lado y ángulo de la bisectriz de la diagonal menor d, respectivamente.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
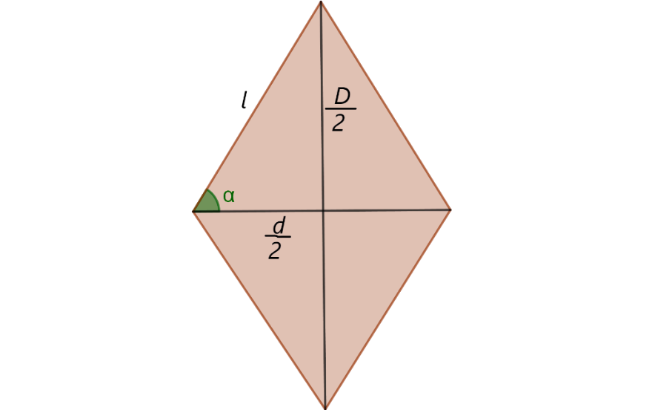
luego
Teorema 6: La diagonal menor de un rombo está dado por
d = 2l cos α
donde l y α son el lado y ángulo de la bisectriz de la diagonal menor d, respectivamente.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
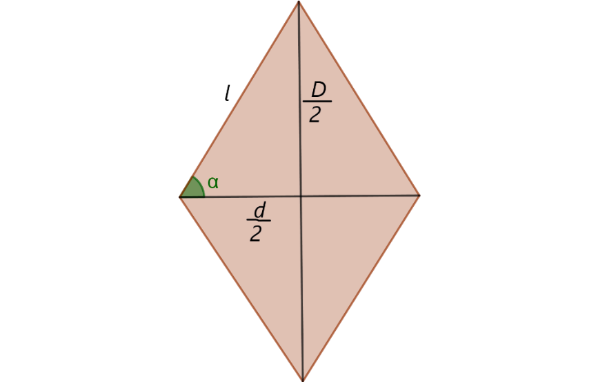
se tiene, por definición de la función coseno
Luego,
2l cos α=d
Teorema 7: El lado de un rombo está dado por
donde D y d son la diagonal mayor y menor respectivamente del rombo.
Demostración 1:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
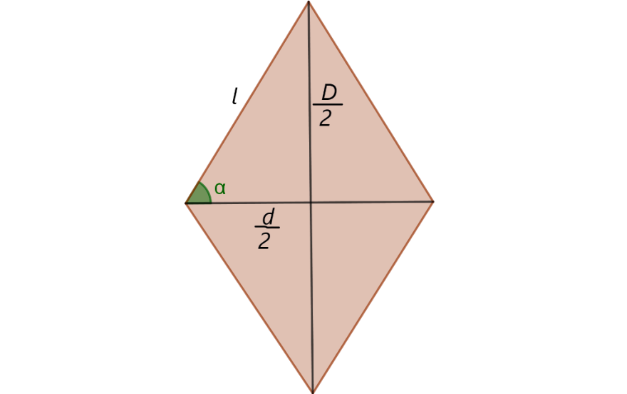
por teorema de Pitágoras (Zill, 2012), se tiene
Demostración 2:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente

por Teorema del Coseno (Zill, 2012), se tiene
Teorema 8: El lado de un rombo está dado por
donde D y α son la diagonal mayor y ángulo de la bisectriz de la diagonal menor d, respectivamente.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
por definición de la función cosecante (Zill, 2012), se tiene
csc α=l/(D/2)
luego
csc α=2l/D
De donde
l=1/2 D csc α
Teorema 9: El lado de un rombo está dado por
l=1/2 d sec α
donde d y α son la diagonal menor y ángulo de la bisectriz de la diagonal menor d, respectivamente.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
por definición de la función secante (Zill, 2012), se tiene
De donde
Teorema 10: El área de un rombo está dado por
donde D y d son las diagonales mayor y menor respectivamente del rombo y α es el ángulo de la bisectriz de la diagonal menor.
Demostración:
De acuerdo a la figura, donde D/2 y d/2 son las semi mitades de las diagonal mayor y menor respectivamente
Utilizando la fórmula del área de un rombo en función del lado y de la bisectriz de la diagonal menor
Entonces, sabiendo que el lado de un rombo está dado por
Luego, al elevar al cuadrado esta última expresión, se tiene
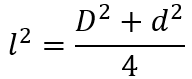
Al sustituir en la fórmula del área en función del lado, obtenemos
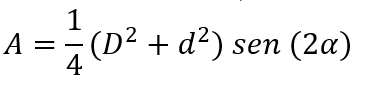
Teorema 11: El producto de las diagonales de un rombo está dado por
D x d=2A
donde D y d es la diagonal mayor y menor respectivamente del rombo
Demostración:
De la fórmula del área de un rombo, se tiene
Luego
D x d=2A
Teorema 12: El producto de las diagonales de un rombo está dado por
D x d=2l2 sen (2α)
donde l y α son el lado y ángulo de la bisectriz de la diagonal menor, respectivamente.
Demostración:
Sabemos que
d = 2l cos α
D = 2l sen α
luego, utilizando la fórmula del seno doble
D x d = (2l sen α) (2l cos α )
D x d = 2l2 (2 sen cos α )
D x d = 2l2 sen (2α)
Teorema 13: La suma de los cuadrados de las diagonales de un rombo está dado por
D2+ d2 = 4l2
donde l es un lado del rombo.
Demostración:
Sabemos que
d = 2l cos α
D = 2l sen α
luego, elevando al cuadrado las expresiones anteriores, obtenemos
d2 = 4l2 cos2 α
D2 = 4l2 sen2
sumando término a término y utilizando la Identidad Pitagórica Fundamental (Zill, 2012)
d2 + D2 = 4l2 cos2 α + 4l2 sen2 α
D2 + d2 = 4l2 (cos2 α + sen2 α)
D2 + d2 = 4l2
Los resultados obtenidos como teoremas del área disciplinar geometría, muestran diferentes variantes demostrativas que permitieron combinar teoría trigonométrica y geométrica. Es necesario e importante señalar que se obtuvieron los siguientes resultados:
Uso de la teoría trigonométrica para demostrar variante de teoremas de cálculo de área, longitudes de diagonales y lado del rombo.
Se desarrollaron 13 demostraciones matemáticas, mediante la combinación de teoría trigonométrica y geométrica.
Uso del Teorema del Coseno y Pitágora en algunas de las demostraciones desarrolladas.
CONCLUSIONES
Las principales conclusiones del presente trabajo se pueden resumir por:
- Aplicación de principios fundamentales matemáticos en el desarrollo constructivo de un teorema, mediante argumentación explicativas y lógicas.
- Aplicación de diferentes métodos demostrativos en las construcciones de las demostraciones matemáticas.
- Aplicación de simbología, técnicas matemáticas y teoría combinada de trigonometría y geometría, en el discurso demostrativo de los teoremas desarrollados.
- Codificación de todos los teoremas demostrados en la investigación mediante el lenguaje de programación Python.
BIBLIOGRAFÍA
Barnet, R. (1991): Geometría, segunda edición. Editorial Mc Graw Hill. México.
Orozco, I. J. (2022). Acerca de la diagonal del Cuadrado. Revista de Divulgación y Prensa, FAREM-Chontales.
Orozco, I. J. (2022). Área del Rectángulo y Triángulo Equilátero. Revista de Divulgación y Prensa, FAREM-Chontales
Swokowski, E., Cole, J. (2009) Álgebra y Trigonometría con Geometría Analítica. 12a Edición. Thomson, México. 2006.
Zill, D., Deward, J. (2012): Álgebra, Trigonometría y Geometría Analítica, tercera edición, Colombia, editorial McGraw Hill.
ANEXOS
Codificación en Python
"""
Created on Fri Apr 22 14:44:26 2022
@author: JUDITH OROZCO e IVAN CISNEROS
"""
#Definición de Librerías en Python
import math
import numpy as np
#Definición de Funciones en Python
def area1(D,d):
return((D*d)/2)
def lado(D,d):
return(math.sqrt(((D/2)**2+(d/2)**2)))
def ang(D,d):
return (math.degrees(math.atan((D/2)/(d/2))))
def lado1(D):
return (1/2*D*(1/math.sin(np.radians(ang(D,d)))))
def lado2(d):
return (1/2*d*1/math.cos(np.radians(ang(D,d))))
def area2(D,d):
return (round(lado(D,d)**2*np.sin(2*math.radians(ang(D,d))),0))
def area3(D,d):
return (1/2*d**2*np.tan(math.radians(ang(D,d))))
def area4(D,d):
return (1/2*D**2*1/np.tan(math.radians(ang(D,d))))
def Dm(D,d):
return(2*lado(D,d)*np.sin(math.radians(ang(D,d))))
def dm(D,d):
return(2*lado(D,d)*np.cos(math.radians(ang(D,d))))
def Dd(D,d):
return(2*lado(D,d)**2*np.sin(2*math.radians(ang(D,d))))
def Dsumad(D,d):
return(4*lado(D,d)**2)
# Impresión de Resultados de acuerdo a los teoremas establecidos
D=float(input("Entre el valor de la diagonal mayor : "))
print()
d=float(input("Entre el valor de la diagonal menor : "))
print()
print("El area del Rombo es : ", area1(D,d))
print()
print("El valor del lado es : ", lado(D,d))
print()
print("El valor del angulo es : ", ang(D,d))
print()
print("El valor del lado es : ", lado1(D))
print()
print("El valor del lado es : ", lado2(d))
print()
print("El area del Rombo es : ", area2(D,d))
print()
print("El area del Rombo es : ", area3(D,d))
print()
print("La Diagonal mayor es : ", round(Dm(D,d),0))
print()
print("La Diagonal menor es : ", dm(D,d))
print()
print("Producto de diagonales : ", round(Dd(D,d),0))
print()
print("Suma de diagonales al Cuadrado : ", round(Dsumad(D,d),0))
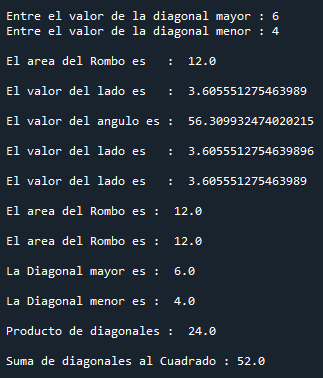
Resultados en la Consola de Python
© 2022 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.


