Algoritmos de Ecuaciones no Lineales por Polinomios de Adomian

Algorithms of Nonlinear Equations by Adomian Polynomials

 

Dicson Antonio Méndez López
Licenciado en Física Matemática, UNAN-Managua, FAREM-Matagalpa
https://orcid.org/0000-0003-2910-3794
dicsonml@yahoo.es

Iván Augusto Cisneros Díaz
Doctor en Matemática Aplicada, UNAN-Managua
https://orcid.org/0000-0003-2014-1946
ivan.cisneros@unan.edu.ni

 

Recibido

28/02/2022

Aceptado

19/07/2022

 

RESUMEN

Este trabajo se realizó con el objeto de mejorar y optimizar los procesos iterativos de aproximación de soluciones a ecuaciones no lineales. El método de Newton es un algoritmo iterativo que permite resolver estos tipos de ecuaciones. La investigación desarrollada consistió en encontrar nuevos esquemas y métodos iterativos equivalente o superiores en el número de iteraciones al método de Newton. Este artículo científico plantea la relación natural que existe entre los Métodos de Descomposición de Adomian y la Técnicas Iterativa Variacional, estableciendo los vínculos matemáticos desarrollados en ambas esferas del conocimiento. Para las demostraciones de los nuevos esquemas y métodos iterativos se basó en el esquema de los Polinomios de Adomian y luego se combinó con las técnicas iterativas variacional, obteniéndose de estas maneras nuevas fórmulas iterativas de cálculo de raíces de ecuaciones no lineales. En todos los casos se utilizó una función auxiliar familia de las funciones exponenciales, ya que tienen la particularidad de ser funciones C^∞. El objetivo principal es demostrar dichas fórmulas iterativas y mostrar que la teoría matemática desarrollada en este campo científico, están fundamentadas teóricamente y analíticamente por métodos y procedimientos lógicos, que permiten desarrollar nuevos esquemas, métodos y técnicas iterativas. Los algoritmos son generados mediante los procedimientos de los Polinomios de Adomian y la Técnica Iterativa Variacional. Este trabajo presenta tres algoritmos nuevos que permiten encontrar las soluciones a ecuaciones no lineales en una cantidad menor de iteraciones que el método de Newton y por lo tanto son más eficientes que dicho método. Todos estos algoritmos fueron programados en el lenguaje de programación Python y se utilizó el paradigma de programación orientado a objetos (POO). Todos estos nuevos algoritmos presentan convergencia en dicha solución. Las ideas de este trabajo pueden extenderse para generar nuevos algoritmos con los Método de Abbasbandy y Cisneros en la búsqueda de algoritmos más eficientes.

 

PALABRAS CLAVES

Método de Newton; Polinomios de Adomian; Iteración Variacional; Algoritmos Iterativos.

 

ABSTRACT

This work was carried out in order to improve and optimize the iterative processes of approximation of solutions to nonlinear equations. Newton's method is an iterative algorithm that allows solving these types of equations. The research developed consisted in finding new schemes and iterative methods equivalent or superior in the number of iterations to Newton's method. This scientific article raises the natural relationship that exists between the Adomian Decomposition Methods and the Variational Iterative Techniques, establishing the mathematical links developed in both spheres of knowledge. For the demonstrations of the new schemes and iterative methods it was based on the Adomian Polynomial scheme and then combined with the iterative variational techniques, obtaining in these ways new iterative formulas for calculating the roots of nonlinear equations. In all cases an auxiliary function of the exponential function family was used, since they have the particularity of being functions C^∞. The main objective is to demonstrate these iterative formulas and to show that the mathematical theory developed in this scientific field is theoretically and analytically based on logical methods and procedures, which allow the development of new schemes, methods and iterative techniques. The algorithms are generated by means of the procedures of the Adomian Polynomials and the Variational Iterative Technique. This work presents three new algorithms that allow finding solutions to nonlinear equations in fewer iterations than Newton's method and therefore are more efficient than Newton's method. All these algorithms were programmed in the Python programming language and the object-oriented programming (OOP) paradigm was used. All these new algorithms show convergence in such a solution. The ideas of this work can be extended to generate new algorithms with the Abbasbandy and Cisneros Method in the search for more efficient algorithms.

 

KEYWORDS

Newton's Method; Adomian Polynomials; Variational Iteration; Iterative Algorithms.

 

INTRODUCCIÓN

 

Es indudable que la Matemática genera un gran impacto en la sociedad actual así lo atestigua el progreso descrito por los modelos matemáticos basados en teoría de funciones, ecuaciones lineales y no lineales, tópicos de álgebra lineal y álgebra abstracta. Así que el estudio de la teoría de ecuaciones es muy importante y como es comprensible, la generación de métodos numéricos para resolverlas constituye un reto importante para los matemáticos actuales.

El estudio de las ecuaciones es tan antiguo como las Matemáticas mismas, pero a medida que la ciencia fue avanzando también se fue necesitando ecuaciones más complejas, que no presentan una solución que se puede determinar mediante una simplificación algebraica. El método de Newton permitió generar soluciones a diversas ecuaciones, y existía al mismo tiempo otros métodos que presentaban convergencia en una cantidad de iteraciones similar al método de Newton.

El estudio de los polinomios de Adomian permitió a Abbasbandy desarrollar un algoritmo efectivo que mejora al método de Newton. Cisneros (2017) hizo importantes avances en este campo y logró desarrollar métodos numéricos sumamente precisos que requerían menos iteraciones que el método de Newton.

En muchos casos estas ecuaciones no tienen una solución exacta y se necesitan métodos aproximados como el método de Newton que permite obtener aproximaciones a las raíces de una ecuación de una forma práctica y eficiente, pero que puede mejorarse de distintas formas, como se ha demostrado en otros trabajos.

Es necesario destacar que existen diversos procesos matemáticos que permiten resolver ecuaciones no lineales, sin embargo, existe la posibilidad de estudiar el análisis de convergencia de dichos métodos, mediante técnicas iterativas, las cuales permiten optimizar de manera eficiente la solución numérica de dichas ecuaciones.

Esto justifica una investigación que permita diseñar nuevos algoritmos basado en la Técnica de Descomposición de los Polinomios de Adomian y de las Técnicas Iterativas Variacional, que permita resolver ecuaciones no lineales en la línea de investigación del Álgebra y Análisis Matemático, y de esta forma establecer un conjunto de algoritmos que permitan generalizar el método de Newton y codificar estos algoritmos en programas computacionales, tal como el lenguaje de programación Python.

 

MATERIALES Y MÉTODOS

 

Se destacan los diferentes algoritmos que combinan el esquema de los Polinomios de Adomian con las Técnicas Iterativas Variacional.

1. La metodología empleada en este trabajo siguió las siguientes etapas:
2. Revisión bibliográfica sobre diversos artículos científicos sobre los Polinomios de Adomian y las Técnicas Iterativas Variacional.
3. Estudio de diversos procedimientos matemáticos que incluye los Polinomios de Adomian y las Técnicas Iterativas Variacional.
4. Formulación de nuevos esquemas y algoritmos iterativos.
5. Programar los algoritmos en Python.
6. Comparar la cantidad de iteraciones.

 

RESULTADOS Y DISCUSIÓN

 

El método de Newton puede expresarse como

Se puede considerar la siguiente notación Por lo tanto el método de Newton está dado por

Los polinomios de Adomian se construyeron para resolver ecuaciones diferenciales, pero tienen otros usos como ayuda al diseño de esquemas iterativos.

Para los fines de este trabajo se considera la ecuación no lineal 𝑓(𝑥) = 0, 𝛼 ∈ ℝraíz de multiplicidad 1 de 𝑓. Según Cisneros (2017, p.52) el método consiste en construir una función en la forma

donde 𝑐 es una constante y 𝑁 es una función no lineal.

Y se crea a partir de ℎ una serie infinita en la forma,

y la función no lineal 𝑁 se descompone como

a los términos 𝐴𝑛 se les llama polinomios de Adomian y están dados por la siguiente serie general

El método de Newton puede expresarse mediante los polinomios de Adomian como:

Donde A0 sería el primer polinomio de Adomian

y, además

Siguiendo un proceso similar al seguido por Cisneros (2017), se deriva A₁ para obtener el segundo término de los polinomios de Adomian.

Por lo tanto

Nuevamente, para obtener el tercer coeficiente

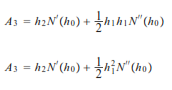
Considerando que

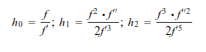
Y, además

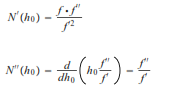
Por lo tanto, el tercer término de Adomian se obtiene mediante el siguiente razonamiento.

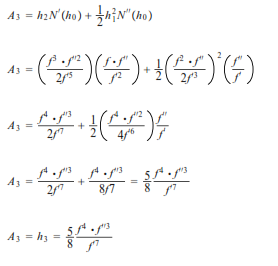
Para el cuarto término, se sabe que

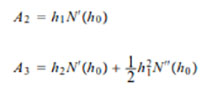
luego

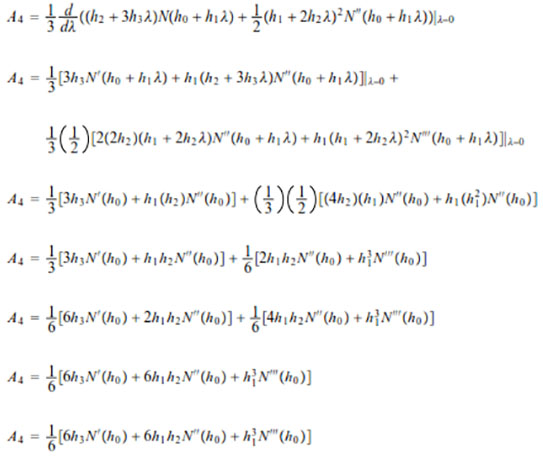
Como

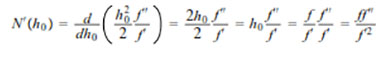
Entonces

Por lo tanto,

Si se tiene presente los valores de h obtenidos anteriormente

Al sustituir resulta

Para encontrar A₅ se tiene que

Por lo tanto

Hasta el momento se tiene que

los valores de h son

y

Como

Se simplifica A₅ como

Como un análisis final se presenta el resumen de la discusión anterior, en forma de los polinomios de Adomian.

Mediante los polinomios de Adomian se generaron los siguientes algoritmos, los cuales fueron presentados en diversos artículos por diferentes autores:

1) Método de Newton, considerando el primer término de los polinomios de Adomian.

Sustituyendo A₀ resulta

2) Método de House Holder.

Considerando el segundo término de Adomian el cual es

Y como

Entonces se obtiene el método de House Holder

Existen diversos análisis de este método, aunque su deducción no se basa precisamente en los polinomios de Adomian, se hace mención en el artículo de Bahgat y Hafiz (2014, p.87).

3) Método de Abbasbandy.

Si se añade el tercer término

de Adomian.

Entonces se logra demostrar el método de Abbasbandy

Los siguientes algoritmos se llamarán Cisneros-Méndez.

Como es natural la función f(x) a considerar debe ser continua, monótona y derivable, y con f'(x) ≠0 . Si la función f'(x) = 0 los métodos se reducen al método de Newton clásico.

Se considera la siguiente sucesión para construir el primer algoritmo.

1) Método Método de Cisneros-Méndez 1 (Contempla el desarrollo para los cuatros primeros polinomios de Adomian), aquí n = 0,1,2, . . .

2) Método Cisneros-Méndez 2 (Contempla el desarrollo para los cinco primeros polinomios de Adomian) con n = 0,1,2, . . .

Es decir, la serie queda

Y al sustituirse por sus respectivos valores

3) Método Cisneros-Méndez 3 (Contempla el desarrollo para los seis primeros polinomios
de Adomian)

La serie

Entonces si se sustituye resulta el siguiente esquema iterativo:

Donde n = 0,1,2, . . .

Estos tres algoritmos presentas los siguientes resultados:

Se considera la ecuación no lineal
e^-x - x³ = 0

Los principales hallazgos respecto a esta ecuación no lineal son:

El método de Newton alcanza la raíz de dicha ecuación en 5 iteraciones, siendo la raíz real con 15 cifras decimales 0,772882959149210. Se toma como valor semilla a x = 1,5.

El algoritmo Cisneros-Méndez 1, Cisneros-Méndez 2, Cisneros-Méndez 3 generan la solución en 4 iteraciones superando al método de Newton.

Se considera la ecuación no lineal
x³ + 4x² - 10 = 0

Esta ecuación fue usada por Cisneros (2017) y además por Bumbariu (2012, p.277) como ejemplo numérico.

Los principales hallazgos respecto a esta ecuación no lineal son:

El método de Newton alcanza la raíz de dicha ecuación en 5 iteraciones, siendo la raíz real con 15 cifras decimales 1, 365230013414097 . Se toma como valor semilla a x = 1,0.

El algoritmo Cisneros-Méndez 1, Cisneros-Méndez 2, Cisneros-Méndez 3 generan la solución en 3 iteraciones superando en dos iteraciones al método de Newton,

Se considera la ecuación no lineal
e^-x + 2lnx = 0

Los principales hallazgos respecto a esta ecuación no lineal son:

El método de Newton alcanza la raíz de dicha ecuación en 5 iteraciones, siendo la raíz real con 15 cifras decimales 0,798518085322251. Se toma como valor semilla a x = 1,5.

Los algoritmos Cisneros-Méndez 1, Cisneros-Méndez 2, Cisneros-Méndez 3 generan la solución en 3 iteraciones, superando al método de Newton en dos iteraciones.

CONCLUSIONES

 

Las conclusiones referentes a la presente investigación se pueden sistematizar en las siguientes aseveraciones:

Generación de nuevos esquemas iterativos que representan 3 nuevas variantes del método de Newton por medio de la Descomposición de los Polinomios de Adomian.
Existencia de nuevos algoritmos, que constituyen variantes del método de Newton que superan al método clásico en el número de iteraciones necesarias para la obtención de una raíz simple.

 

REFERENCIAS BIBLIOGRÁFICAS