Modelamientos de los parámetros geofísicos por una fuente sísmica capaz de generar un tsunami en la costa de Pochomil, Nicaragua
Modeling of geophysical parameters by a seismic source capable of generating a tsunami off the coast of Pochomil, Nicaragua
Humberto García Montano
Departamento de Física, Facultad de Ciencias e Ingeniería. Universidad Nacional Autónoma de Nicaragua, Managua, UNAN-Managua, Nicaragua.
https://orcid.org/0000-0001-9049-0274
hgarciamontano@gmail.com
Ninoska J. Maltez Perez
Graduada de la carrera de Licenciatura en Física Mención Geofísica del Departamento de Física, Facultad de Ciencias e Ingeniería, Universidad Nacional Autónoma de Nicaragua, Managua, UNAN-Managua, Nicaragua
https://orcid.org/0000-0002-9513-8517
caprijeannette@gmail.com
Recibido
11/11/2021
Aceptado
12/03/2022
RESUMEN
En esta investigación, los parámetros geofísicos (golpe, deslizamiento, inclinación, buzamiento, tipo de falla, rigidez, profundidad, dinámica de ruptura sísmica, generación y propagación de tsunamis) del movimiento del suelo debido a un terremoto de deslizamiento de bloque como el ocurrido en 1992 frente a la costa de León. Estos parámetros están asociados a movimientos verticales y horizontales tridimensionales del suelo dependientes del tiempo de modelos de ruptura dinámica espontánea que conducen a la generación de un tsunami como amenaza latente para la costa de Pochomil. Para ello se utilizó el software TUNAMI-N2 Code modificado por Yanagisawa (2018), basado en los parámetros geofísicos calculados por el Servicio Geológico de los Estados Unidos (USGS), el Global Centroid-Moment-Tensor Project (GCMT), y Tanioka et al. 2017, con magnitud 7,7 Mw. De los resultados del modelado, el evento que genera una onda de mayor amplitud fue causado por un plano de falla inversa, con magnitud 8.0 Mw, rigidez 15 GPa, profundidad 10 km, buzamiento 80.8°, inclinación 87.2° y deslizamiento 118°. El modelo de propagación de olas generó una altura de 14,2 m y un tiempo de llegada de 35 minutos.
PALABRAS CLAVES
Tsunami; golpe; buzamiento; deslizamiento; magnitud; profundidad; rigidez.
ABSTRACT
In this investigation, the geophysical parameters (strike, slip, dip, fault type, stiffness, depth, seismic rupture dynamics, tsunami generation and propagation) of ground motion due to a block-slip earthquake such as the one that occurred in 1992 off the coast of Leon. These parameters are associated with three-dimensional vertical and horizontal time-dependent ground motions of spontaneous dynamic rupture models leading to the generation of a tsunami as a latent threat to the Pochomil coast. For this purpose, the TUNAMI-N2 Code software modified by Yanagisawa (2018) was used, based on the geophysical parameters calculated by the United States Geological Survey (USGS), the Global Centroid-Moment-Tensor Project (GCMT), and Tanioka et al. 2017, with magnitude 7.7 Mw. From the modeling results, the highest amplitude wave generating event was caused by a reverse fault plane, with magnitude 8.0 Mw, stiffness 15 GPa, depth 10 km, dip 80.8°, dip 87.2°, and slip 118°. The wave propagation model generated a height of 14.2 m and an arrival time of 35 minutes.
KEYWORDS
Tsunami; strike; dip; slip; rake; magnitud; profundidad; rigidez
INTRODUCCIÓN
La generación de tsunamis a partir de deformaciones del lecho marino inducidas por terremotos se ha reconocido desde hace mucho tiempo como un peligro importante para las zonas costeras. En general, se ha considerado que las fallas por deslizamiento de impacto son insuficientes para desencadenar grandes tsunamis, incluso a través de la generación de deslizamientos de tierra submarinos.
Los movimientos del suelo verticales y horizontales tridimensionales dependientes del tiempo de los modelos de ruptura dinámica espontánea se utilizan para impulsar los movimientos de los límites en el modelo de tsunami. Los resultados sugieren que las rupturas por cizallamiento que se propagan a lo largo de fallas de deslizamiento, atravesando bahías estrechas y poco profundas, son las principales candidatas para la generación de tsunamis. El enfoque dinámico y los grandes desplazamientos horizontales, característicos de los terremotos de deslizamiento en fallas largas, son factores críticos del peligro de tsunami. Estos hallazgos apuntan a mecanismos intrínsecos para la generación considerable de tsunamis por fallas de deslizamiento, que no requieren fuentes sísmicas complejas, deslizamientos de tierra o batimetría complicada (Elbanna. et al, 2021).
Los terremotos que ocurren por fallas en las zonas de subducción también han generado tsunamis devastadores en campo cercanos (Satake y Tanioka, 1999). Estos incluyen fallas de separación por el empuje entre placas, fallas de empuje e inversión en el arco posterior (por ejemplo, Mar de Japón), las fallas normales en la elevación exterior de la placa de subducción causadas por tensiones de flexión (por ejemplo, en la costa de Sanriku, Japón e Islas Kuriles), las fallas de buzamiento y deslizamiento intraarco (por ejemplo, el Pasaje de Mona frente a la costa de Puerto Rico) y terremotos más profundos que ocurren dentro de la placa de subducción (Tanioka et al., 1995).
Varios estudios han indicado conectividad entre estos tipos de fallas, en términos de la evolución de la tensión durante el ciclo sísmico (Taylor, M. A. J., Dmowska, R., and Rice, J. R). Por ejemplo, se ha observado que los terremotos con fallas normales en la elevación exterior pueden ocurrir después de grandes terremotos por el empuje entre placas, debido a los efectos de transferencia de tensión (Polet y Thio, 2003). Además, la complejidad geométrica entre estas fallas a menudo se pasa por alto y puede dar lugar a rupturas sísmicas compuestas que pueden ser difíciles de clasificar entre las descripciones de fallas descritas anteriormente (Baba et al., 2005).
La Zona de Subducción es la fuente de mayor producción de sismos; más del 90% de los sismos que registra la red sísmica local de Nicaragua proceden de este sector, que cubre 120 km mar adentro, aproximadamente, y una franja costera de 50 km, aproximadamente, desde el litoral del Pacífico hasta el arco volcánico (Segura, 2016).
El terremoto de Nicaragua del 2 de septiembre de 1992 generó tsunamis que causaron grandes daños en la costa del Pacífico de Nicaragua a pesar de su moderada magnitud de onda superficial (Ms 7.2). Estudios de campo para la intensidad sísmica y la altura del tsunami (Abe et al., 1993; Satake et al., 1993) demostraron que la intensidad era muy pequeña (máximo III en la escala de Mercalli modificada) pero la altura del tsunami era tan grande como 9,9 m sobre el nivel medio del mar. El tamaño del terremoto inferido de la intensidad débil es tan pequeño como M = 6, mientras que los tsunamis grandes corresponden a los de un terremoto tan grande como M = 8 (Abe et al., 1993). Estas discrepancias indican que este terremoto fue un terremoto de tsunami inusual (Kanamori, 1972).
El modelado numérico del tsunami de este terremoto ha sido realizado por lmamura et al. [1993] y Titov y Synolakis [1997]. Ambos estudios coincidieron con las alturas de las olas del tsunami registradas a partir de un modelo fuente con un momento sísmico sobre 3 x 1021 N∙m, asumiendo una rigidez estándar de 3-4 x1010 N/m2. Este momento sísmico es un orden de magnitud mayor que el estimado a partir del análisis de ondas sísmicas.
El objetivo de esta investigación es modelar distintos planos de fallas y tipos magnitudes de terremotos que tenga el potencial de generar tsunami he inundaciones frente a la costa de Pochomil. Este trabajo es importante debido a las inundaciones que generan los tsunamis producto de terremotos interplaca, en la zona de subducción del pacífico y pueden causar trágicas pérdidas de vidas y grandes daños materiales en las comunidades costeras.
MATERIALES Y MÉTODOS
De acuerdo con el método de investigación, por la clasificación de Hernández, Fernández y Baptista, el tipo de estudio es correlacional, y según el nivel inicial de profundidad del conocimiento es descriptivo. De acuerdo con el tiempo de ocurrencia de los hechos, el estudio es retrospectivo, por el periodo de secuencia es transversal y según el análisis de alcance es predictivo, la escala de medición es de intervalo, y por su naturaleza y combinación del enfoque su variable es mixta. (Hernández, Fernández, & Baptista, 2014).
Área de estudio
El área de estudio elegido fue la costa de Pochomil se localiza a 65 km de la capital, pertenece al municipio de San Rafael del Sur departamento de Managua en la Figura 1.
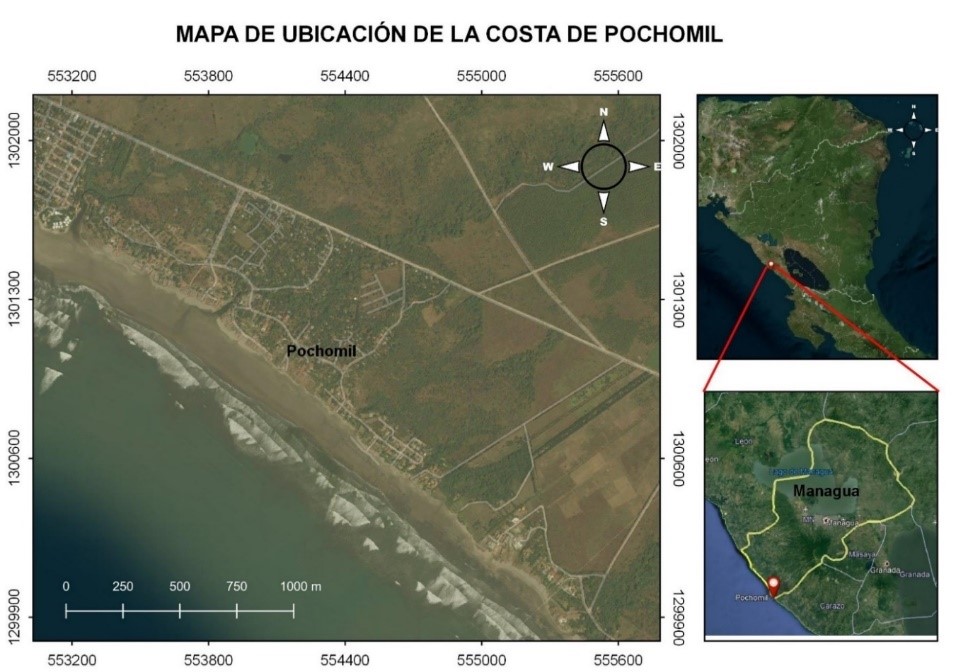
Figura 1. Mapa de localización del área de estudio.
Para esta investigación, se emplearon dos pasos fundamentales:
Mecanismo y parámetros focal del terremoto
Se utilizaron los parámetros sísmicos de Sateke (1994) para calcular la deformación del fondo marino, los ángulos de rumbo (), buzamiento y deslizamiento , la cantidad de deslizamiento, las dimensiones del área de ruptura (largo, L y ancho, w) y la profundidad del terremoto. Para cada escenario, se utilizaron las ecuaciones empíricas para estimar la magnitud del terremoto correspondiente de cada ruptura de falla, seguido del cálculo del ancho de ruptura y el desplazamiento de la superficie (Wells y Coppersmith, 1994), y el momento sísmico escalar .
Para la modelación del sismo precursor, se tomaron las condiciones iniciales del modelo se obtiene de la teoría de deformación para un medio homogéneo y elástico (Okada, 1992), el cual requiere de los parámetros del mecanismo focal del sismo generador. Se propone la deformación del fondo marino (debido al sismo) se traslada (en forma casi instantánea) a la superficie del océano, lo que genera la propagación de las ondas del tsunami. Además, se asume que el plano de falla es un rectángulo de dimensiones L (longitud) por W (ancho), ambas dimensiones con orden de magnitud de cientos de km, Figura 2.
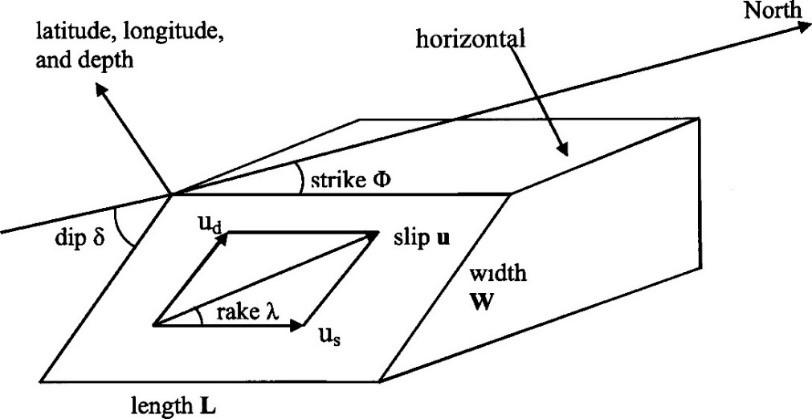
Figura 2. Parámetros del plano de falla. Se representa el bloque que subduce en una falla inversa (Sakate, 2014).
Modelación de tsunami
Para el modelado de tsunami, se realizó por métodos de simulación numérica con el software TUNAMI-N2 Code modificado por Yanagisawa, (2018) para la generación (modelo de fuente sísmica), y propagación (simulación numérica mediante la teoría lineal). Se usaron dos puntos de pronóstico computacional que corresponden al área donde se quiere determinar la altura de la ola. En este caso son frente a Pochomil con las siguientes coordenadas. Lon. 528766.76N, Lat. 1297153.63W, Lon. 531132.99N Lat. 1285775.58W.
RESULTADOS Y DISCUSIÓN
Modelo de falla para la deformación del fondo oceánico.
A partir del momento sísmico se obtuvo la magnitud del momento, el cual es una escala de magnitud introducida por Kanamori, (1977) y Hanks & Kanamori, (1979), con el objetivo de evitar el problema de saturación para eventos sísmicos de larga duración.
Se realizaron cientos de modelaciones variando los diferentes parámetros geofísicos como el tensor momento, el rumbo, el buzamiento, la profundidad, el momento sísmico, dip, slip, strike, rake y rigidez. También, se trabajó con 3 tipos plano de falla: lateral, inversa y normal.
A continuación, se presenta uno de los cientos de tablas de ejemplo con las que trabajaron para determinar las condiciones del sismo precursor que era capaz de generar un tsunami.
En la Tabla 1, se muestran los siguientes datos, en la colunna 1 parámetros geofisicos, en la columna 2 los datos para la falla inversa, en la columna 3 los datos de la falla normal, en la columna 4 los datos de la falla lateral con Rake de -179°.
Tabla 1. Parametros geofisicos y planos de falla, inversa, normal y lateral con Dip = 9.6°.
| Parámetros | Inversa | Normal | Lateral |
|---|---|---|---|
| Strike (°) | 315 | 315 | 315 |
| Dip (°) | 9.6 | 9.6 | 9.6 |
| Rake (°) | 106.9 | -106.9 | -179 |
| Magnitud Mw | 7.7 | 7.7 | 7.7 |
| Profundidad del hipocentro (km) | 10 | 10 | 10 |
| Rigidez (GPa) | 15 | 15 | 15 |
Los parámetros de la Tabla 1 se usaron para los cálculos de entrada al software TUNAMI-N2 Code mostrados en la Tabla 2, los parametros introucidos fueron: dimenciones de la falla, coordenadas geográficas de la esquina de la falla, el deslizamiento del bloque, momento sísmico (columna 1). Ademas, en la columna 2 se muestra los datos calculados de la falla inversa, en la columna 3 los datos calculados de la falla normal y en la columna 4 los datos calculados de la falla lateral.
Tabla 2. Parámetros de entrada para el programa TUNAMI-N2 Code.
| Parámetros | Inversa | Normal | Lateral |
|---|---|---|---|
| Origen de la falla. Lon x | -87.62 | -87.72 | -87.94 |
| Falla. Lat y | 11.05 | 11.06 | 11.01 |
| Profundidad (m) | 8718.37 | 9005.14 | 9297.31 |
| Slip (m) | 5.93 | 6.43 | 6.53 |
| Slip angle (°) | 106.9 | -106.9 | -179 |
| Longitud de la falla (m) | 104472 | 124165 | 172981 |
| Ancho de la falla (m) | 48083 | 37325 | 26363 |
| Área (m2) | 5.0E+09 | 4.6E+09 | 4.6E+09 |
| M0 (N.m) | 4.467E+20 | 4.468E+20 | 4.46E+20 |
Una vez modelados múltiples parámetros (Figura 3), solo se mantuvo constante largo L= 200 km y ancho w = 100 km del bloque Sateke (1994), de lo contrario se fueran generados una gran cantidad modelos que no generaban tsunamis significativos.
Modelación de escenarios de propagación
Con los datos del tsunami ocurridos en Nicaragua de 1992, permitió emplear el modelo de plano de falla para aproximar los resultados de los escenarios a un evento real, el terremoto fue modelado con magnitud de 7.7 Mw como precursor de del tsumani que afecto la costa Pacifica de los deparatmentos de Managua y León. Ademas, se ubicando el epicentro a 92 km de la línea costera, frente la zona a Pochomil en la Zona de Subducción del Pacífico,
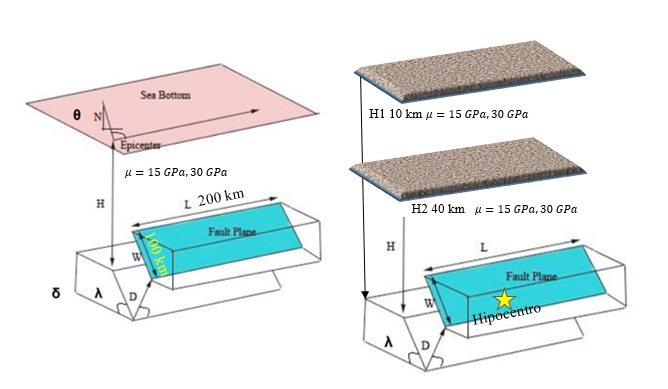
Figura 3. Parámetros de ruptura de fallas (Imamura & Yalciner, 2006).
En la Tabla 2, se muestran las coordenadas computacionales del epicentro para el modelaje de propagación de la ola frente la costa de Pochomil, y las coordenadas correspondientes a los puntos de control para conocer la altura de la ola en la zona de interés ubicado a 50 m de profundidad (H).
| Puntos | Longitud | Latitud |
|---|---|---|
| Epicentro computacional | 469458.94N | 126575.70W |
| Puntos de pronóstico computacional 1 | 528766.76N | 1297153.63W |
| Puntos de pronóstico computacional 2 | 531132.99N | 1285775.58W |
En la Figura 4, se muestra el epicentro del sismo modelado.
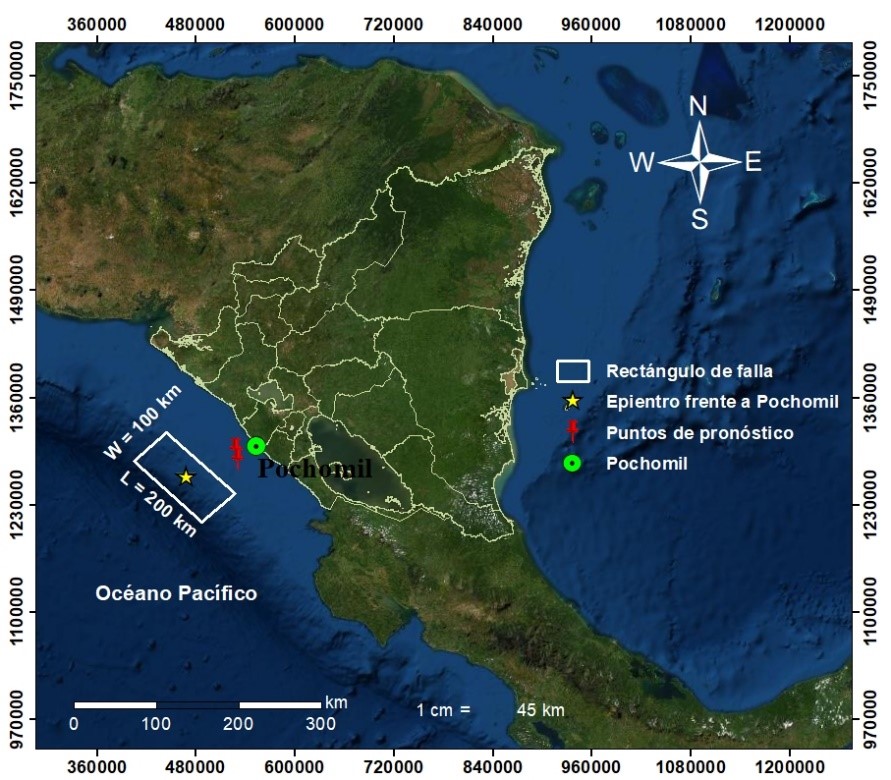
Figura 4: Mapa de fuente sísmica. (Epicentro del sismo para la simulación de tsunami frente la costa de Pochomil) y dimensiones del bloque.
Se realizaron cuatro modelos de propagación de la ola que se detallan acontinuación:
Modelo de propagación 1. Para este modelo se realizo con un Dip de 9.6° y los parametros geofísicos mostrados en la Tabla 1, con cordenadas amteriormente expuestas.
Con los datos generados por el software TUNAMI-N2 Code se realizo el Gráfico 1, el cual muestra los resultado de la modelación de propagación para una magnitud de 7.7 Mw y altura de la ola, con los planos de falla inversa (linea roja), normal (linea azul) y lateral (linea negra).
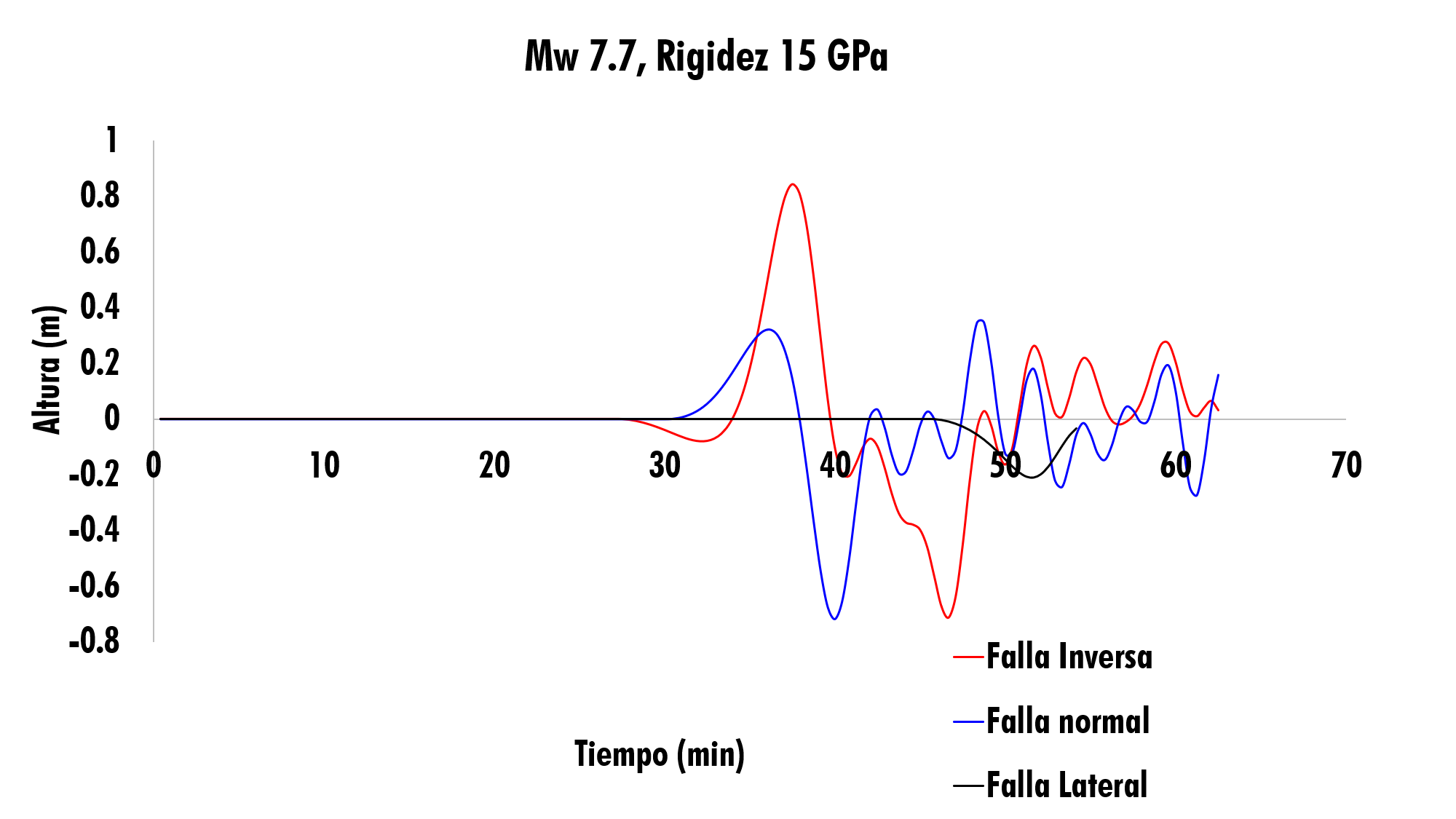
Figura 5. Propagación del tsunami con planos de falla, Inversa, normal y lateral. (Dip =9.6°).
Como se aprecia en la Figura 5, se muestran los resultados de la propagación de la ola para un sismo de 7.7 Mw a una profundidad de 10 km; el modelo de falla inversa (línea roja) produce una perturbación de 0.8 m generando un fuerte oleaje con un tiempo de arribo de la ola de 36.6 min. Mientras la falla normal (línea azul) no provoca una considerable perturbación del agua, por lo cual la altura de la ola generada es de apenas 0.2 m en cuanto al tiempo de arribo es de 36.2 min. Para el caso del plano de falla lateral (línea negra), no produce altura considerable de la ola. También, los resultados muestran que un Dip de 9.6° no genera un desplasamiento vertical suficiente del fondo oceanico que desplace la colunna de agua para generar un tsunami destructivo.
Modelo de propagación 2. Para este modelo, se uso una longitud de la falla, magnitud, rigidez, profundidad constante y con un Dip= 80.8°.
Con los cálculos anteriores se obtuvo la Figura 6, la cual muestra y compara el resultado de propagación de los 3 planos de falla, con Dip= 80.8°. En este gráfico, se presenta el resultado de la modelación de propagación y altura de la ola, debido a un terremoto generado para los 3 planos de falla y Dip= 80.8°.
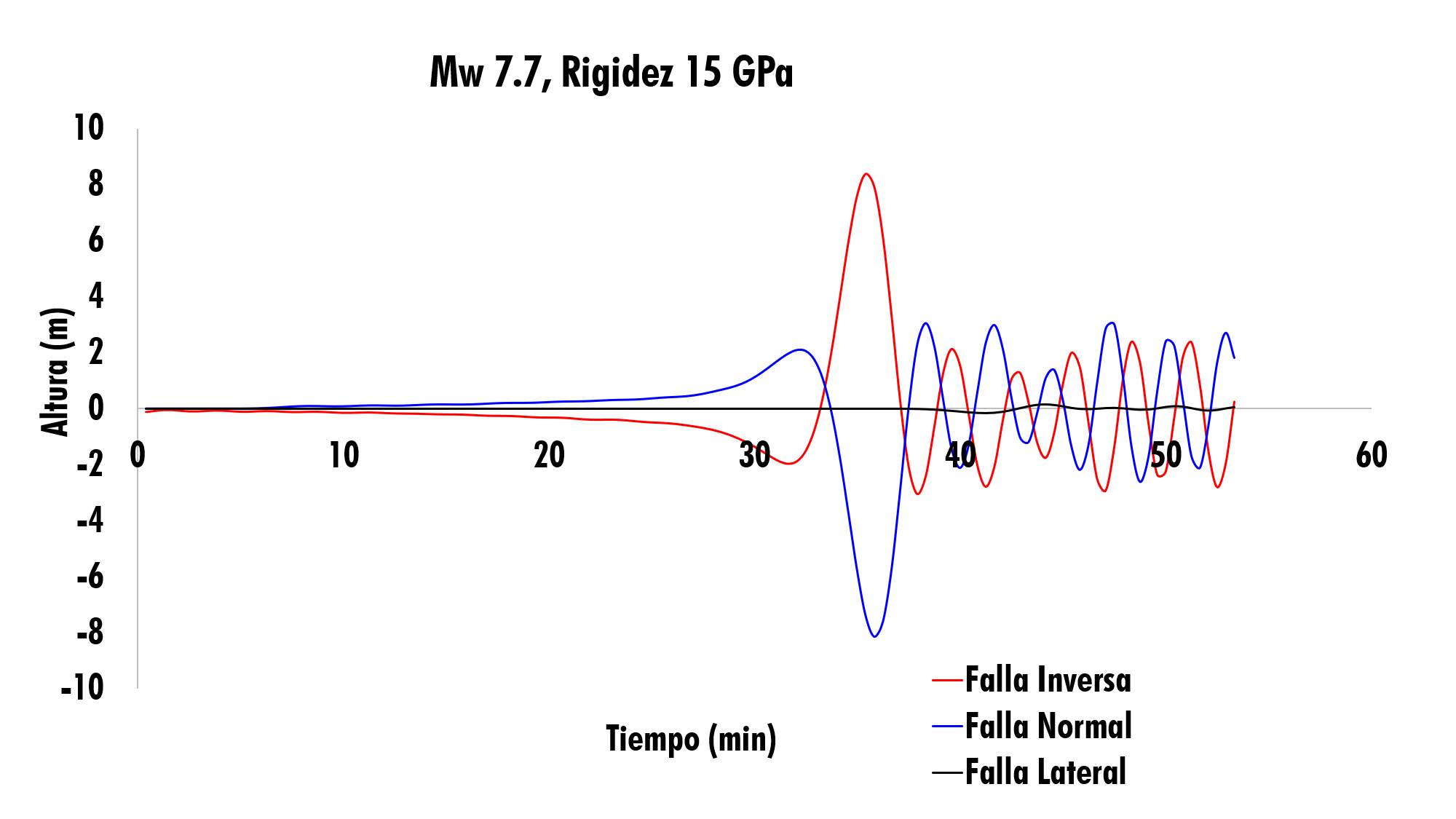
Figura 6. Propagación del tsunami con plano de falla Inversa, Lateral, Normal (Dip=80.8 °).
En la Figura 6, se aprecia la predicción de un tsunami generado por un sismo de 7.7 Mw con ángulo Dip de 80.8°. La falla inversa (línea roja), produce una perturbación vertical con una altura de la ola de 8.3 m y con un tiempo de arribo de la ola de 35.8 min. Mientras, que el tsunami ocasionado por la falla normal (línea azul) el cual produce una ola considerable de 1.7 m y con un tiempo de arribo de la ola de 32.9 min. Sin embargo, la falla lateral generada una altura de la ola (línea negra) de apenas 0.14 m.
Modelo de propagación 3. Para este modelo se uso terremoto de magnitud 7.7 Mw, rigidez (15 GPa), profundidad (10 km) constantes para los 3 planos de falla., y ocn las misma corrdenadas.
En la Tabla 3, se muestran los planos de falla calculados por: USGS, GCTM y Tanioka (2017) para el sismo de 1992 frente a León.
Tabla 3: Parámetros geofÍsicos y plano de falla inversa.
| Fuente | Strik (°) | Dip (°) | Rake (°) |
|---|---|---|---|
| USGS | 130 | 79 | 93 |
| GCTM | 122 | 78 | 90 |
| Tanioka | 118 | 80.8 | 87.2 |
Los parámetros de la Tabla 3 se usaron para los calculos de entrada al software TUNAMI-N2 Code mostrados en la Tabla 4, estos fueron: coordenadas geograficas de la esquina de la falla, dimenciones de la falla, el deslizamiento del bloque, momento sísmico (colunna 1). Ademas, en la columna 2 se muestra los datos de estrada para del modelo de falla de USGS, la columna 3 para los GCMT y en la columna 4 los datos calculados por Tanioka y con epicentro frente a Pochomil.
Tabla 7. Parámetros Geofísicos de las fuentes: USGS, GCTM, Tanioka.
| Parámetros | USGS | GCTM | Tanioka |
|---|---|---|---|
| Origen de la falla. Lon x | -87.62 | -87.62 | -87.62 |
| Falla. Lat y | 11.05 | 11.05 | 11.05 |
| M0 (N·m) | 4.4668E+20 | 4.4668E+20 | 4.4668E+20 |
| Profundidad (m) | 10 000.00 | 10 000.00 | 10 000.00 |
| Slip (m) | 5.93 | 5.93 | 5.93 |
| Slip angle (°) | 79 | 78 | 80.8 |
| Longitud de la falla (m) | 104472 | 104472 | 104472 |
| Ancho de la falla (m) | 48083 | 48083 | 48083 |
| Área (m2) | 5.0E+09 | 5.0E+09 | 5.0E+09 |
Con los resultados del software TUNAMI-N2 Code se realizo la Figura 7, el cual muestra la propagación de la ola y el tiempo de arribo para las tres fuentes sismicas calculadas para el sismo 1992, ubicando el epicentro frente a Pochomil. Además, se muestra la propagación de la ola, la línea color negro representa el resultado del modelo de falla de USGS con 8.0 m la amplitud de la ola, la linea color rojo representa el resultado de la fuente de GCMT con una amplitud de la ola de 8.2 m, y la linea color azul representa la propagación de la fuente de Tanioka con una amplitud de la ola de 8.4 m.
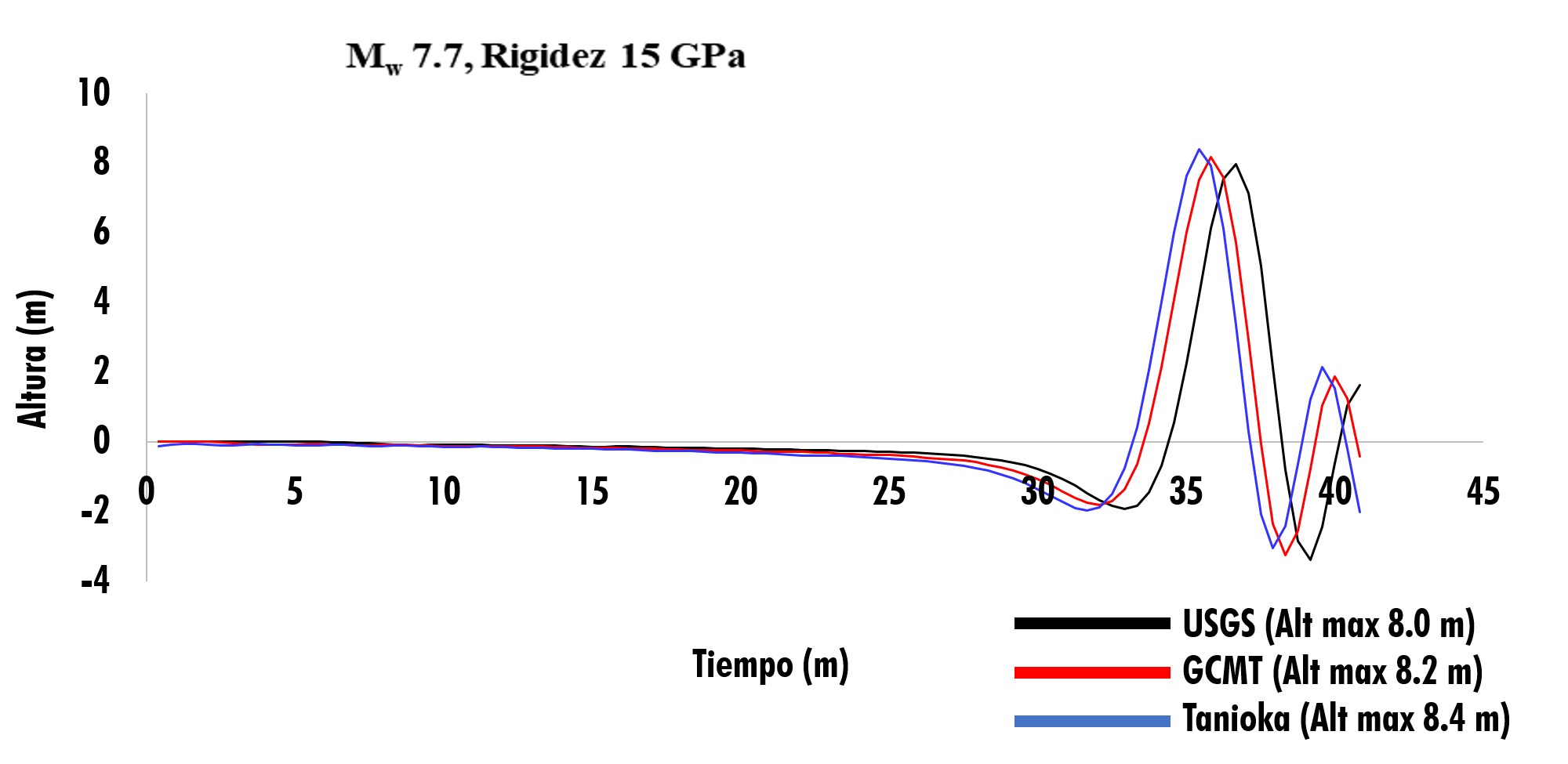
Figura 7. Comparación de la propagación de tsunami de las fuentes: USGS, GCTM, Tanioka. (Mw 7.7, Depth 10 km).
El tiempo de arrivode las olas fue entre 35.8 y 36.2 minutos, los modelos concuerdan con las prediccines de la altura de la ola para el sismo de 1992, que se observo entre 3 - 7 m, y en algunos puntos de la costa la amplitud de la ola fue de 8 m, 9 m y 10 m, como Marcella y Transito (Sakate et al; 1993) se debe tomar en cuenta que esta vez el sismo se conisdera frente a Pochomil por lo que es concordante con la estimación de la altura del tsunami para esta zona.
De acuerdo a los escenarios anteriores los parámetros de plano de falla inversa (calculados para el sismo de 1992) que generaron mayor amplitud de la ola en los escenarios de propagación, fue el Modelo de Tanioka, (Strike: 118°, Dip: 80.8°, Rake: 87.2°).
Tomando la magnitud del terremoto de 7.7 Mw como referencia al evento del sismo ocurrido en 1992 y 8.0 Mw como un escenario máximo creíble (Tabla 5, columna 1). Además, por cada magnitud se usaron las dos profundidades de origen para los sismos (columna 2) y dos rigideces por cada profundidad (columna 3).
Tabla 5 . Parámetros para escenarios de propagación del tsunami. Por cada magnitud se varía la profundidad y la rigidez.
| Magnitud Mw | Profundidad (km) | Rigidez (GPa) |
|---|---|---|
| 7.7 | 10 | 15 |
| 30 | ||
| 40 | 15 | |
| 30 | ||
| 8.0 | 10 | 15 |
| 30 | ||
| 40 | 15 | |
| 30 |
Modelo de propagación 4. Las condiciones de la Tabla 5 se usaron para calcular los parámetros de entrada con magnitud de 7.7 Mw, con variaciones en la profundidad y rigidez mostrados en la Tabla 6 para generar los nuevos escenarios de propagación.
Tabla 6. Parámetros de entrada al software TUNAMI-N2 Code para un sismo de 7.7 Mw para profundidades de 10 km y 40 km, con rigidez de 15 GPa y 30 GPa.
| Parámetros | 7.7 Mw, Depth 10 km | 7.7 Mw, Depth 40 km | ||
|---|---|---|---|---|
| 15 GPa | 30 GPa | 15 GPa | 30 GPa | |
| Fault origin (lon or x-grid) | -87.62 | -87.62 | -87.62 | -87.62 |
| Fault (lat or y-grid) | 11.05 | 11.05 | 11.05 | 11.05 |
| Depth (m) | 10 000.00 | 10 000.00 | 29 566.63 | 29 566.63 |
| Slip (m) | 5.93 | 2.96 | 5.93 | 2.96 |
| Slip angle (°) | 87.20 | 87.20 | 87.20 | 87.20 |
| Fault length (m) | 104 472 | 104 472 | 104 472 | 104 472 |
| Fault Width (m) | 48083 | 48083 | 48083 | 48083 |
| Cal área (m2) | 5.0E+09 | 5.0E+09 | 5.0E+09 | 5.0E+09 |
| Mo | 4.47E+20 | 4.47E+27 | 4.47E+20 | 4.47E+20 |
En la Figura 8 se muestra el resultado de la propagación de la ola y el tiempo de arribo, generado por un sismo de magnitud 7.7 Mw, a una profundidad de 10 km. La curva azul muestra la propagación de la ola, para una rigidez de 15 GPa, generando una altura máxima de 8.4 m, y un tiempo de arribo de 35.8 min. La curva roja muestra una altura de 4.1 m, para una rigidez de 30 GPa y, el tiempo de llegada de la ola es de 35.8 min.
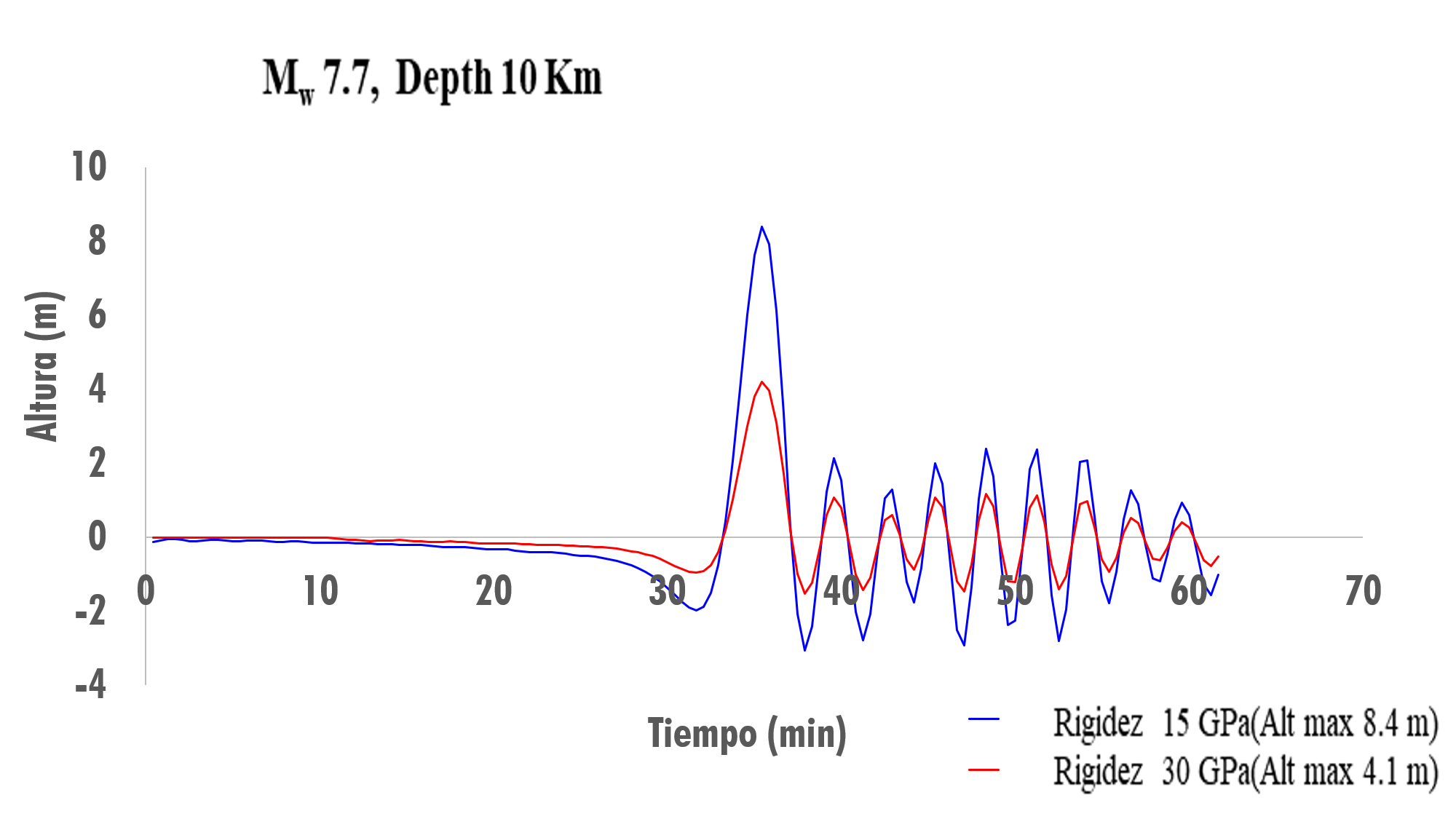
Figura 8. Propagación de la ola con 7.7 Mw, Depth 10 km (15 GPa y 30 GPa).
El presente Figura 9, se muestra la propagación de la ola y el tiempo de arribo, generado por un sismo de magnitud 7.7 Mw, a una profundidad de 40 km. La curva azul muestra la propagación de la ola, para una rigidez de 15 GPa, con una altura máxima de 4.11 m, y un tiempo de arribo de 35.4 min. La curva roja muestra la propagación de la ola, para una rigidez de 30 GPa, donde el resultado la altura de la ola es de 2.1 m, y, el tiempo de llegada de la ola es de 35.4 min.
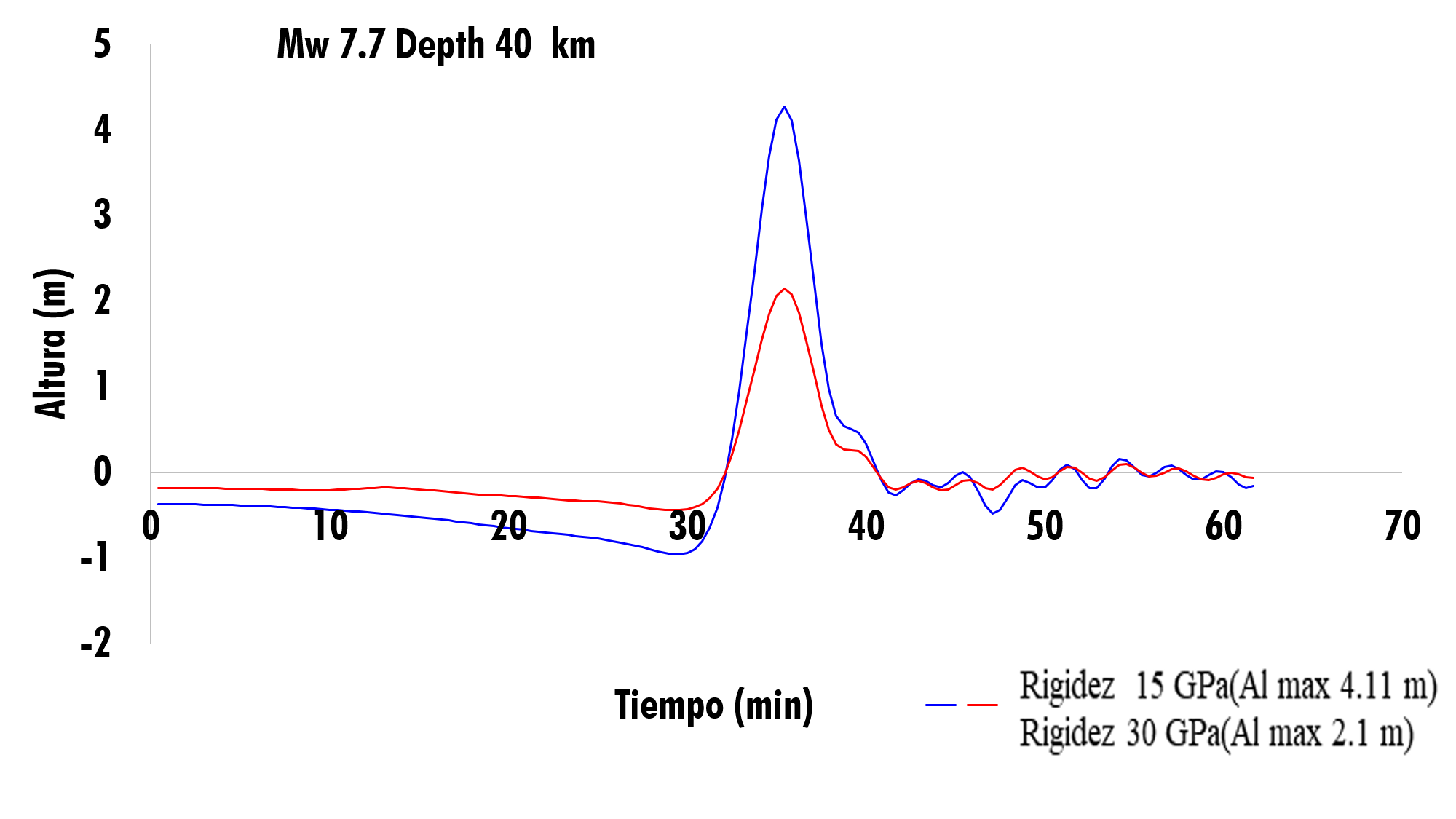
Figura 9. Propagación de la ola con 7.7 Mw, Depth 40 km (15 GPa y 30 GPa).
Con las condiciones de la Tabla 7 se calcularon los parámetros de entrada con magnitud de 8.0 Mw, con variaciones de la profundidad y rigidez mostrados en la Tabla 7, para generar los nuevos escenarios de propagación.
Tabla 7. Parámetros de entrada al software TUNAMI-N2 Code para un sismo de 8.0 Mw para profundidades de 10 km y 40 km, con rigidez de 15 GPa y 30 GPa.
| Parámetros | 8.0 Mw, Depth 10 km | 8.0 Mw, Depth 40 km | ||
|---|---|---|---|---|
| 15 GPa | 30 GPa | 15 GPa | 30 GPa | |
| Fault origin (lon or x-grid) | -87.79 | -87.79 | -87.79 | -87.79 |
| Fault (lat or y-grid) | 10.88 | 10.88 | 10.88 | 10.88 |
| Depth (m) | 10 000.00 | 10 000.00 | 25 664.12 | 25 664.12 |
| Slip (m) | 8.20 | 4.10 | 8.20 | 4.10 |
| Slip angle (°) | 87.2 | 87.2 | 87.2 | 87.2 |
| Fault length (m) | 154 881 | 154 881 | 154 881 | 154 881 |
| Fault Width (m) | 66 069 | 66 069 | 66 069 | 66 069 |
| Cal área (m2) | 1.02E+10 | 1.02E+10 | 1.02E+10 | 1.02E+10 |
| M0 | 1.26E+21 | 1.26E+21 | 1.26E+21 | 1.26E+21 |
El presente Figura 10, muestra la propagación de la ola y el tiempo de arribo, generado por un sismo de magnitud 8.0 Mw, a una profundidad de 10 km. La curva azul muestra la propagación de la ola, para una rigidez de 15 GPa, resultando una altura máxima de 14.09 m, y un tiempo de arribo de 36.66 min. La curva roja muestra la propagación de la ola, para una rigidez de 30 GPa, en la que se obtuvo una altura máxima de 6.9 m, y el tiempo de llegada de la ola es de 38.0 min.
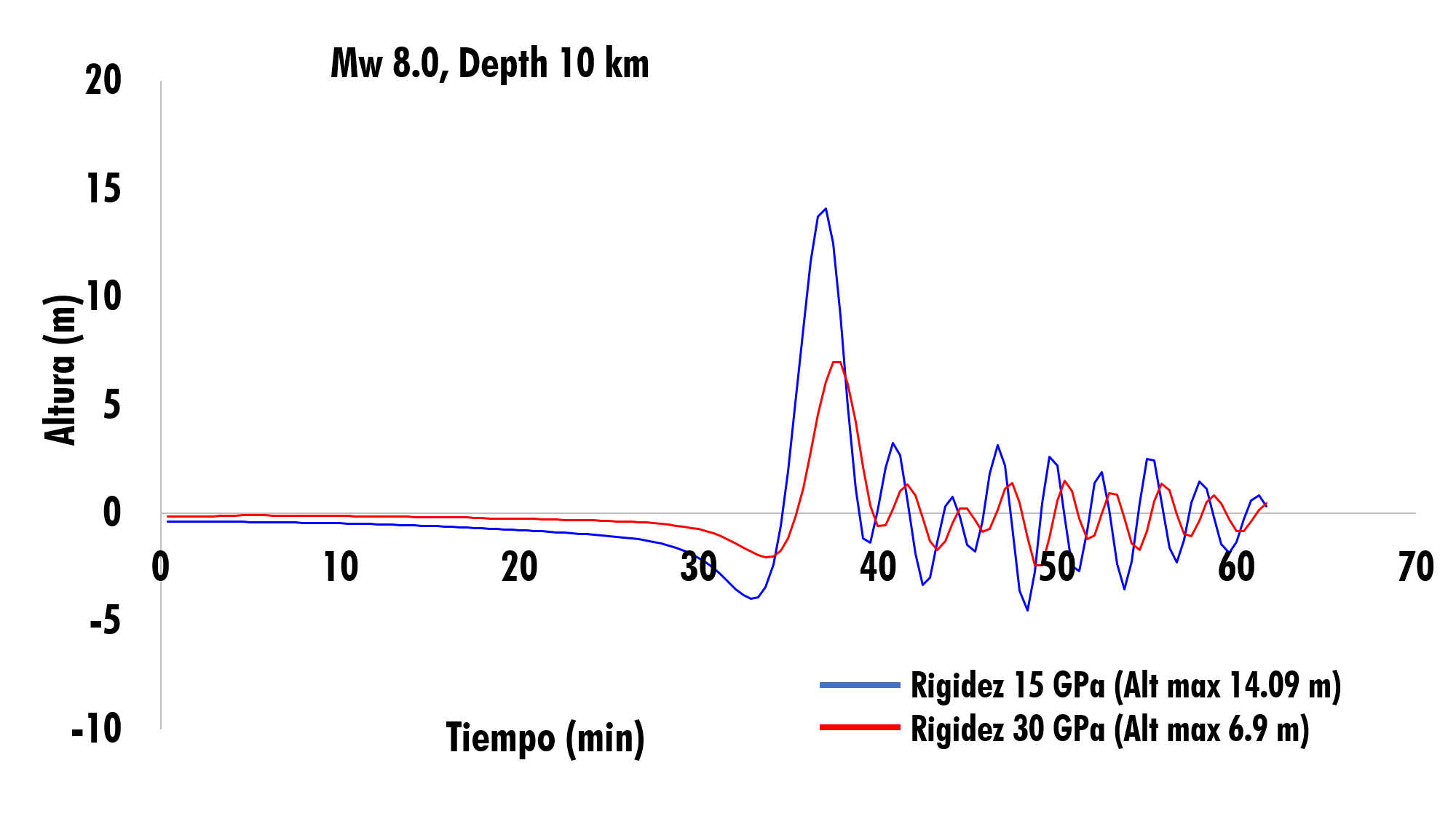
Figura 10. Propagación de la ola con 8.0 Mw, Depth 10 km (15Gpa y 30 GPa).
En la Figura 10 a continuación, se muestra la propagación de la ola y el tiempo de arribo, generado por un sismo de magnitud 8.0 Mw, a una profundidad de 40 km. Donde la curva azul muestra la propagación de la ola, para una rigidez de 15 GPa, dando como resultado una altura máxima de 8.4 m, y un tiempo de arribo de 37.9 min. La curva roja muestra la propagación de la ola, para una rigidez de 30 GPa, en la que se obtuvo una altura máxima 5.6 m, y el tiempo de llegada es de 38.3 min.
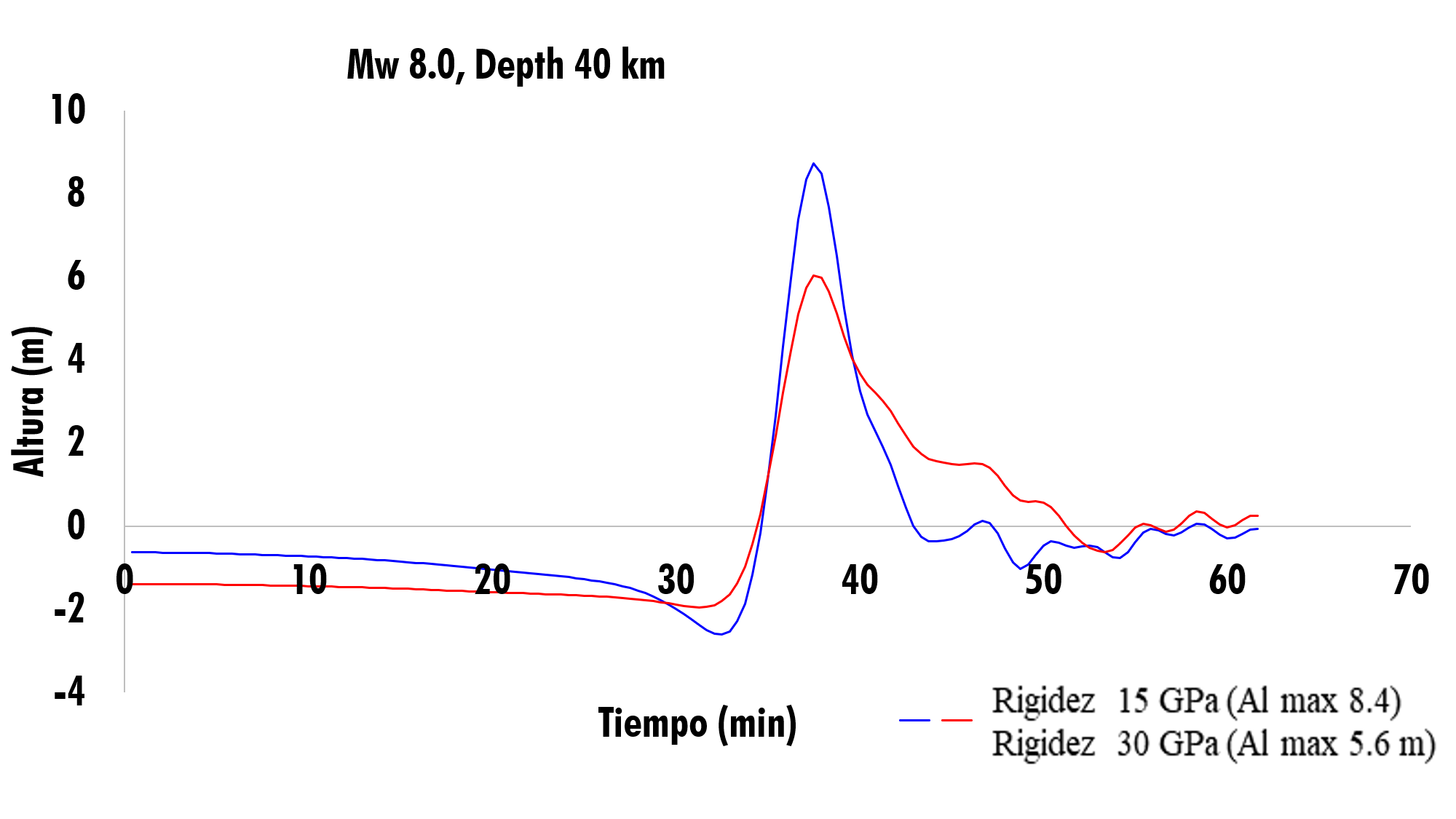
Figura 10 . Propagación de la ola con 8.0 Mw, Depth 40 km (15 GPa y 30 GPa).
Para esta investigación se realizon con datos topográficos y batimétricos que se encontraban disponible, no se tuvo acceso a batimetría y topografía de mejor resolución para el área de interés. Usamos el conjunto de datos de batimetría general del océanos de GEBCO, con un espacio de cuadrícula de 1 minutos de arco y espaciado de cuadrícula de 30 segundos de arco.
Se trabajaron los tres tipos de plano de falla: normal, lateral e inversa, en todos los modelos asociados a los parametros geofisicos con una rigidez entre 15 GPa a 30 GPa lo cual corresponde a los datos de Tanioka (2017). Además, se mantuvo constante largo y ancho del bloque Sateke (1994). Debido a que solo variar esto parámetros generarían cientos de modelaciones que podría ser importante o no.
De la modelación y cálculos de los parámetros geofísicos, encontramos que la combinación de los elementos Strike con angulo menores a 100°, Dip menores a 60° y Rake menor a 45° no produjeron olas significativas, ni si quiera de 1 metro de altura en el programa Tunami-N2 code.
De acuerdo a los escenarios anteriores y el parámetro de plano de falla inversa fue el que genero la mayor altura de la ola, tomando como referencia el Modelo de Tanioka, (Strike: 118°, Dip: 80.8°, Rake: 87.2°).
En cuanto a los sismos de 5 hasta 6.5 de magnitud, no generaron ninguna perturbación. Esto está ampliamente comprobado con los sismos que ocurren en la zona de subducción y concuerdan con los parámetros del evento que genero el tsunami en León calculado por Tanioka. Los sismos de magnitud 7 generaron olas considerables de aproximadamente mayor a 1 metro. Mientras, que aquellos sismos de 7.7 de magnitud como referencia al evento ocurrido del sismo de 1992 y 8.0 de magnitud como un escenario máximo creíble.
Es importante tener en cuenta, que la zona de subducción se caracteriza por la mayor ocurrencia de sismos a profundidades entre los 10 km y los 40 km (Wiemer y Zuniga 1994; Wiemer 2001). Desde el tiempo generado por el sismo hasta la llegada de las olas tarda en promedio 35 minutos, por lo que, que es importante un buen sistema de alarma que emita el aviso cuando mucho a los 10 minutos de ocurrencia.
CONCLUSIONES
De los resultados de modelación, se concluye que el evento geológico sismogénico capaz de generar tsunamis de grandes proporciones es el plano de falla inversa con los siguientes parámetros geofísicos con magnitud 8.0 Mw, rigidez 15 GPa, profundidad 10 km, Dip, 80.8, Rake 87.2, y slip 118. El modelo propagación de la ola género una altura de 14.2 m y tiempo de arribo de 36.6 minutos.
Se determina la importancia de tener presente cuando ocurran terremotos con magnitud 7 Mw a más, debido a que estos pueden generar tsunamis con olas mayores a 8 metros.
Recomendamos realizar una nueva modelación con una nueva versión del software disponible y batimetría con mejor resolución, realizar modelos de amenaza de tsunamis, para mostrar con más detalle el posible comportamiento de las inundaciones en las comunidades costeras expuestas a este tipo de amenaza. Además, mejorar las modelaciones para todas las costas de Nicaragua, con el fin de brindar herramientas para los diversos estudios de base científica, y/o proyectos académicos con estudiantes de la carrera de Ingeniería en Geofísica.
BIBLIOGRAFÍA
Abe, F. (1989): "Deformation characteristics of sand in plane strain compression at small strain levels," Master thesis, University of Tokyo (in Japanese).
Ambraseys, N. (1962). Data for the investigation of the seismic sea waves in the Eastern. Bull. Seis. Soc. Amer., 52(4), 895-913.
Argüello, G. (2016). W phase inversion analysis and tsunami simulation for tsunami warning for large earthquake (mw > 7.0) in Nicaragua. Managua.
Baba, T., and Cummins, P. R. (2005), Contiguous rupture areas of two Nankai Trough earthquakes revealed by high-resolution tsunami waveform inversion, Geophys. Res. Lett., 32, L08305, doi:10.1029/2004GL022320.
Borrero, J., Kalligeris, N., Lynnet, P., Fritz, H., Newman, A., & Convers, J. (2014). Observations and Modeling of the August 27, 2012, Earthquake and Tsunami affecting El Salvador and Nicaragua. Springer Base.
Cabrera, A. (2018). Tsunami Characteristics of outer-rise Eaerthquakes along the pacific coast of Nicaragua - A Case study for the 2016 Nicaragua Event-. Managua, Nicaragua. MEE16718.
Cardona, O., Yamín, L., Bernal, G., Ordaz, S., Reinoso, A., Barbat, B., & Carreño, T. (2008). Amenaza por tsunami en Miramar. Managua.
Castillo. (2017). Geología de la Región Pacífica de Nicaragua. Managua: – ISSN 2164-4268.
Elbanna, A., Abdelmeguid, M., Ma, X., Amlani, F., Bhat, H. S., Synolakis, C., & Rosakis, A. J. (2021). Anatomy of strike-slip fault tsunami genesis. Proceedings of the National Academy of Sciences, 118(19)
Espín, R. (2012). La Física de los Tsunamis.
Fernandez, M., Molina, E., Havscov, J., & Atakan, K. (2000). Tsunamis and Tsunami Hazards in Central America.
Goto, C. O. (1997). TIME Project: Numerical Method of Tsunami Simulation with the Leap-Frog Scheme. Intergovernmental Oceanographic Commission of UNESCO, Manuals and Guides 35, Paris.
Güendel, F., & Protti, M. (1998). Sismicidad y sismotectónica de América Central. Física de La Tierra.
Gusiakov, K. (2016). Tsunami history - recorded. Rusia.
Hanks, T., & Kanamori, H. (1979). A moment magnitude scale. Geophys.
Imamura. (1942). History of Japanese tsunamis. Kayo-No-Kagaku (Oceanography). Japón.
Imamura, F. S. (1993). Estimate of the Tsunami Source of the 1992 Nicaraguan Earthquake from. Tokyo.
Imamura, F., & Yalciner, A. (2006). Tsunami modelling manual (tunami model). Japón.
INETER. (2019). Boletín Sismológico, Vulcanológico y Geológico. Dirección General de Geología y Geofísica. Managua: Apdo.2110.
Linsley, R; Franzini, B; (1979) Water Resourses Engineering Third Edition. Mcgraw-Hill Series in Water Resources Engineering.
Kajiura, K. (1963). The leading wave of tsunami, Bull. Earthq. Tohoku.
Kanamori, H. (1972). Mechanism of tsunami earthquakes. Physics of the earth and planetary interiors, 6(5), 346-359.
Kanamori, H. (1977). The energy reléase in great earthquakes. Geophys.
Koshimura, S. (2009). Developing fragility functions for tsunami damage estimation using numerical model and post-tsunami data from banda aceh, indonesia. Tohoku.
Koshimura, S. (2009) TUNAMI-CODE, Tohoku University’s Numerical Analysis Model for Investigation of Tsunami, JST-JICA Perú Project, Disaster Control Research Center, Tohoku University.
Lana, X., & Correig, A. (1981). Determinación de la longitud de falla y velocidad de ruptura. Barcelóna.
Leeds, D. (1974). Catalog of Nicaraguan Earhguakes. Am., 64, 1153- 1158.
Levin, B., & Nosov, M. (2009). Physics of Tsunamis. Rusia.
Lida, K. (1963). Magnitude, energy and generation mechanisms of tsunamis and a catalogue of.
Mansinha, L., & Smylie, D. (1971). The displacement Fields of Inclined Faulds: Bulletin of the Seismological Society of America.
Minster, J., & Jordan, H. (1978). present-day plate motions. J.G Res., 83, 5331 -52554.
Molina, E., Marroquín, G., Escobar, J., Talavera, E., Rojas, W., Climent, A., Lindholm, C. (2008). Proyecto resis II. Evaluación de la Amenaza Sísmica en Centroamérica.
Niemeyer, H. (1999). Apuntes de geologia estructural. Antofagasta.
Okada, Y (1992) Internal deformation due to shear and tensile faults in a half space, Bull. Seismol. Soc. Am. 82(2), 1018 -1040.
Papadopoulos, G., & Imamura, F. (2001). A proposal for a new tsunami intensity scale. In: Proceedings of International Tsunami Symposium. Seattle, U.S.A., 569-577.
Polet, J., & Thio, H. K. (2003). The 1994 Java tsunami earthquake and its “normal” aftershocks. Geophysical Research Letters, 30(9).
Rojas, W. (1993). Catálogo de sismicidad histórica y reciente de América Central. Desarrollo y Análisis Tesis de Licenciatura en Geología, Universidad de Costa Rica.
Sakate, K. (2014). Advances in earthquake and tsunami sciences and disaster risk reduction since the 2004 Indian ocean tsunami.
Satake, K. (1994). Mechanism of the 1992 Nicaragua tsunami earthquake. En geophysical research letters, vol. 21 (pág. No.23). Michigan: PAGES 2519-2522.
Segura, F. (2008). Algunas características de la subducción frente a Nicaragua. UNAN-Managua.
Segura, F. (2013). Reseña de la sismicidad en Nicaragua. Managua.
Segura, F. (2016). Reseña de la sismicidad en Nicaragua con énfasis en la Depresión Nicaragüense. Managua.
Segura, F & Rojas, W. (1987). Amenaza sísmica para el Centro de la ciudad de Managua Nicaragua.
Shipley, T., & Moore, G. (1990). Sediment accretion, subduction, and dewatering at the base trench sople off Costa Rica: A seismic reflection view of the décollement, - Geophys. Res., 21.
Shuto, N. (1993). Tsunami intensity and disaster. In: Tsunamis in the World. S.Tinti, . Kluwer Academic Publisher, Dordrecht.
Sieberg, A. (1927). Geologische, physikalische und angewandte Erdbeben Kunde. Verlag von Gustav Fischer, Jena.
Tanioka, Y., & Argüello, G. (2017). Method to Determine Appropriate Source Models of Large Earthquakes Including Tsunami.
Tanioka, Y., Grillo, U., & Argüello, G. (2019). Pronóstico de inundación de tsunami casi en tiempo real para América Central: estudio de caso del terremoto de tsunami de Nicaragua en 1992. Managua.
Taylor, M. A. J., Dmowska, R., and Rice, J. R. (1998), Upper plate stressing and seismicity in the subduction earthquake cycle, J. Geophys. Res., 103(B10), 24523– 24542, doi:10.1029/98JB00755.
Titov, V. V., & Synolakis, C. E. (1997). Extreme inundation flows during the Hokkaido‐Nansei‐Oki tsunami. Geophysical Research Letters, 24(11), 1315-1318.
Tristan, J. (1916). The Costa Rica Earthquake of february 27, 1916 Bull. Seism. Soc. Am. V6, pp. 232-235.
Wells, D. L., & Coppersmith, K. J. (1994). New empirical relationships among magnitude, rupture length, rupture width, rupture area, and surface displacement. Bulletin of the seismological Society of America, 84(4), 974-1002.
Wiemer, S. (2001). A software package to analyze seismicity: ZMAP. Seismol. Res. Lett., 72, 3, 373-382.
Wiemer, S., & Zuniga, R. (1994). ZMAP - a software package to analyze seismicity, EOS, Transactions, Fall Meeting. AGU, 75, 456.
Yanagisawa, H. (2018). Lecture notes on Numerical simulation of tsunami inundation and its application, IISEE/BRI.
© 2022 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
