Comparación estadística de dos técnicas metrológicas para la estimación de la incertidumbre de medición de una metodología analítica implementada en el laboratorio de aguas naturales del CIRA - UNAN-Managua
Statistical comparison of two metrological techniques for the estimation of the measurement uncertainty of an analytical methodology implemented in the laboratory of natural waters of the CIRA - UNAN-Managua
Jonathan Herrera M.1
jonathan.herrera@cira.unan.edu.ni
Recibido: 04 de junio de 2020, Aceptado: 24 de junio de 2020
1 Nicaraguan Aquatic Resources Research Center at the National Autonomous University of Nicaragua (CIRA-UNAN). Managua, Nicaragua
RESUMEN
En las diferentes metodologías de ensayos implementadas en los laboratorios a nivel internacional, existe cierta duda de la validez de los resultados reportados, por lo tanto, como requisito es obligatorio para todos los laboratorios que pretenden acreditarse de acuerdo a la norma ISO 17025, contar con una base teórica y técnica confiable para “estimar” dicha duda denominada incertidumbre de la medición. En éste sentido el laboratorio de Aguas Naturales del CIRA-UNAN-Managua desarrolló una comparación metrológica, utilizando como punto de partida un método de ensayo validado y dos técnicas para estimar la incertidumbre (método GUM y método Kragten) ambas técnicas consisten en la definición clara del mensurando y comprensión del procedimiento de medición. La comparación metrológica consistió en tomar el método GUM estableciendo que magnitudes influyen en la medición, definiendo un modelo matemático que relacione las magnitudes de entrada con el mensurando, determina coeficientes de sensibilidad y finalmente estimar la incertidumbre utilizando la ley de propagación de las incertidumbres. Por otro lado Kragten se utilizó un método numérico de diferenciación que permite visualizar las componentes de mayor influencia de forma que sólo se requiere conocer la forma de obtener el resultado final.
Palabras clave: técnica; quimiometría; incertidumbre; evaluación.
ABSTRACT
In the different testing methodologies implemented in laboratories at the international level, there is some doubt about the validity of the reported results, therefore, as a requirement is mandatory for all laboratories that intend to be accredited according to ISO 17025, to have a reliable theoretical and technical basis to “estimate” such doubt called measurement uncertainty. In this sense, the CIRA-UNAN-Managua Natural Waters laboratory developed a metrological comparison, using as a starting point a validated test method and two techniques for estimating uncertainty (GUM method and Kragten method) both techniques consist of the clear definition of measuring and understanding of the measurement procedure. Metrological comparison consisted of taking the GUM method by establishing which magnitudes influence measurement, defining a mathematical model that relates input magnitudes to measuring, determines sensitivity coefficients, and finally estimates uncertainty using the law of spread of uncertainties. On the other hand, Kragten used a numerical method of differentiation that allows visualizing the components of greater influence so that only requires knowledge of how to obtain the final result.
Keywords: technique; chemometry; uncertainty; evaluation.
INTRODUCCIÓN
Ciertamente, la medida en química siempre ha sido el campo de actuación de la química analítica. La quimiometría trata, específicamente, de todos aquellos procesos que transforman señales analíticas y datos más o menos complejos en información, utilizando métodos de origen matemático, estadístico y otros procedentes del campo de la lógica formal para conseguir sus resultados. Por lo que, la quimiometría se sitúa en un campo interdisciplinar. Aunque sus métodos y herramientas provienen de otras disciplinas claramente los fines de la quimiometría están ligados a la química y su éxito depende de los problemas dados dentro de un laboratorio químico.
En este sentido la metrología es probablemente la ciencia más antigua en el mundo, y aún hoy en día pocos la conocen al igual que la relevancia de esta ciencia y su incidencia en la economía y la sociedad la cual se trata de una ciencia básica, que juega un papel importante en el campo de la investigación medioambiental, industrial, médica, etc. El vocabulario internacional de metrología define a esta como la ciencia de las mediciones y sus aplicaciones (VIM 2.2), incluyendo todos los aspectos teóricos y prácticos de las mediciones, cualesquiera que sean su incertidumbre de medida y campo de aplicación.
La evolución en el tratamiento de la incertidumbre de medida, desde el enfoque “del error” (algunas veces llamado enfoque tradicional o enfoque sobre el valor verdadero) hacia el enfoque “de la incertidumbre”, ha obligado a reconsiderar ciertos conceptos al igual que generar técnicas para la estimación de dicha desviación. La desviación respecto al valor verdadero está constituida por errores sistemáticos y aleatorios, admitiéndose que siempre es posible distinguir entre sí estos dos tipos de errores, y que deben tratarse de manera diferente. No existe una regla que indique cómo combinarlos en un error total que caracterice el resultado de medida dado, obteniéndose únicamente un valor estimado. En general, solo es posible estimar un límite superior del valor absoluto del error total denominado, en forma un tanto inapropiada, “incertidumbre”.
El objetivo de las mediciones en el enfoque “de la incertidumbre” no es determinar el mejor valor verdadero posible. Se supone más bien que la información obtenida de la medición permite únicamente atribuir al mensurando un intervalo de valores razonables, suponiendo que la medición se ha efectuado correctamente.
La moción en este estudio es basada en que actualmente los laboratorios a nivel nacional como a nivel internacional deben demostrar la competencia técnica analítica en que sus métodos analíticos proporcionan resultados fiables y adecuados para su finalidad y propósito debido a que muchas de las decisiones tomadas están fundadas en la información que estos datos proporcionan.
MATERIALES Y MÉTODOS
El presente estudio es de carácter descriptivo ya que describe el comportamiento específico de cada una de las variables metrológicas las cuales son el resultado de la implementación de modelos matemáticos y estadísticos aplicados dentro del control de calidad analítico de una metodología o ensayo. Asimismo se encuadra un enfoque cuantitativo donde se observó el protagonismo de los elementos numéricos los cuales permitieron lograr un conocimiento comprobable del objeto en cuestión.
Para este estudio se utilizaron instrumentos como: 1) Bureta de 10 ml previamente calibrada, 2) Materiales de Referencia Certificados, 3) Pipetas volumétricas y Matraces de aforo serializados y con certificados de calibración, 4) El procedimiento de determinación de dureza total por el método titrimétrico del ácido etilendiamino tetraacético (EDTA) en agua potable y natural descrito en el Standard Methods for the examination of water and wastewater. (2012). 22nd. Edition. Washington: APHA con código 2340.C., 5) la guía GUM (2008), guía EURACHEM /CITAC (2012).
Tratamiento analítico de la muestra
El ácido Etilendiamino tetraacético (EDTA) y sus sales de sodio forman un complejo soluble quelato, la reacción ocurre cuando se añaden a una solución de ciertos cationes metálicos. Si se añade una pequeña cantidad de un colorante, tal como el Negro de Eriocromo a una solución acuosa que contiene iones de Ca y de Mg con un pH de 10,0 ± 0,1, la solución se torna o vira a un color rojo vino. Si el EDTA es agregado como un titulante, se forman complejos de Ca y Mg y cuando todo el Mg y Ca han sido acomplejados, la solución cambia de color de rojo vino a azul, marcando el punto final de la reacción.
Se elabora 1000 ml de muestra con una concentración teórica de 162,00 mg.l-1 como CaCO3 a la cual se le realizan 10 determinaciones de Dureza Total tomando 50 ml de la misma, seguidamente de la titulación de los 50ml de muestra, la expresión de los resultados se da por medio del siguiente modelo matemático:
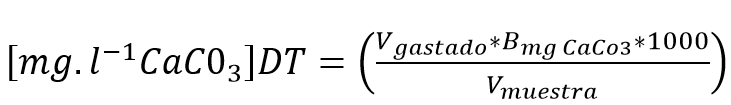 Ecuacion #1
Ecuacion #1
Tratamiento metrológico de las mediciones
Descripción de la técnica de GUM
GUM utiliza una serie de pasos en las que va describiendo la estimación de la incertidumbre de medición dentro de los pasos se mencionan: Descripción general de la medición, modelo de evaluación, información de las magnitudes de entrada, incertidumbre típica de las magnitudes de entrada, combinación de los valores e incertidumbres, estimación de la incertidumbre expandida y finalmente el reporte del resultado.
Al utilizar la metodología de GUM, se tomará en cuenta el expresar y como una función de las variables xi, es decir: 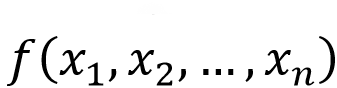 . Las magnitudes de entrada
. Las magnitudes de entrada
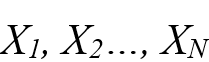 , de las que depende la magnitud de salida pueden ser consideradas a su vez como mensurando, pudiendo depender de otras magnitudes, junto con las correcciones y factores de corrección de los efectos sistemáticos, llegándose así a una relación funcional f. Posteriormente se estima la incertidumbre típica u(xi) de las variables xi, seguidamente de la determinación de los coeficientes de sensibilidad por derivación parcial ci de la forma:
, de las que depende la magnitud de salida pueden ser consideradas a su vez como mensurando, pudiendo depender de otras magnitudes, junto con las correcciones y factores de corrección de los efectos sistemáticos, llegándose así a una relación funcional f. Posteriormente se estima la incertidumbre típica u(xi) de las variables xi, seguidamente de la determinación de los coeficientes de sensibilidad por derivación parcial ci de la forma:
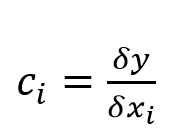 Ecuacion #2
Ecuacion #2
Los datos obtenidos anteriormente consistirán en un número de contribuciones cuantificadas de la incertidumbre total, sea asociada con fuentes individuales o con efectos combinados de diferentes fuentes. Las contribuciones tienen que ser expresadas como desviaciones estándares y combinadas de acuerdo a las reglas apropiadas para dar una incertidumbre estándar combinada.
El resultado de la combinación de las contribuciones de todas las fuentes es la incertidumbre estándar combinada uc(y), la cual contiene toda la información esencial sobre la incertidumbre del mensurando y la contribución ui(y) de cada fuente a la incertidumbre combinada depende de la incertidumbre estándar u(xi) de la propia fuente y del impacto de la fuente sobre el mensurando. Es posible encontrar que una pequeña variación de alguna de las magnitudes de influencia tenga un impacto importante en el mensurando, y viceversa. Se determina ui(y) por el producto de u(xi) y su coeficiente de sensibilidad ci:
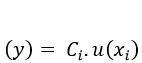 Ecuacion #3
Ecuacion #3
La incertidumbre combinada uc (y) se calcula por la suma geométrica de las contribuciones particulares:
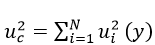 Ecuacion #4
Ecuacion #4
Considerando las 2 ecuaciones anteriores obtenemos:
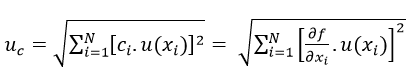 Ecuacion #5
Ecuacion #5
La incertidumbre típica de y, siendo y la estimación del mensurando; es decir, el resultado de medida, se obtiene componiendo adecuadamente las incertidumbres típicas de las estimaciones de entrada x1, x2,..., xN. Esta incertidumbre típica combinada de la estimación y se denota como uc( y).
La incertidumbre típica combinada uc(y) es la raíz cuadrada positiva de la varianza combinada u2c (y), dada por:
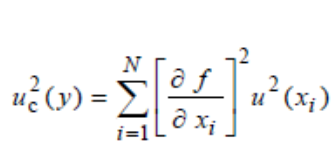 Ecuacion #6
Ecuacion #6
Dónde: f es la función dada en la ecuación (4). Cada u(xi) es una incertidumbre típica evaluada como se describe en la evaluación Tipo A o evaluación Tipo B.
La incertidumbre típica combinada uc(y) es una desviación típica estimada y caracteriza la dispersión de los valores que podrían ser razonablemente atribuidos al mensurando y.
En particular, la variación de y producida por una pequeña variación Δxi en la estimación de entrada xi y viene dada por: (Δy)i = ( ∂ f/ ∂ xi) (Δxi). Si esta variación es debida a la incertidumbre típica de la estimación xi, la variación correspondiente de y es (∂ f/ ∂ xi) u(xi). La varianza combinada uc (y) puede considerarse entonces como una suma de términos, cada uno de ellos representando la varianza estimada asociada a y, debido a la varianza estimada asociada a cada estimación de entrada xi. Esto conduce a escribir la ecuación (3) en la forma:
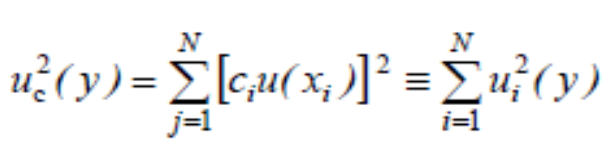 Ecuacion #7
Ecuacion #7
 Ecuacion #8
Ecuacion #8
La ecuación (3) y las derivadas de ella, tales como las ecuaciones (7) y (8), son válidas solamente si las magnitudes de entrada Xi son independientes o no correlacionadas (las variables aleatorias, no las magnitudes físicas que se supone son invariables) Si algunas de las Xi están correlacionadas significativamente, es imprescindible tener en cuenta las correlaciones.
Cuando las magnitudes de entrada están correlacionadas, la expresión adecuada para la varianza combinada u2c(y) asociada al resultado de medida es: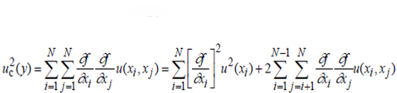 Ecuacion #9
Ecuacion #9
Dónde: xi y xj son las estimaciones de Xi y Xj, y u(xi, xj) = u(xj, xi) es la covarianza estimada asociada a xi y xj. El grado de correlación entre xi y xj viene dado por el coeficiente de correlación estimado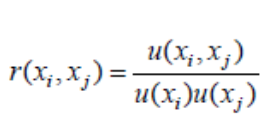 Ecuacion #10
Ecuacion #10
Dónde: r(xi, xj) = r(xj, xi) y −1 ≤ r(xi, xj) ≤ +1. Si las estimaciones xi y xj son independientes, r(xi, xj) = 0, y una variación en una de las dos no implica una variación en la otra.
El término de covarianza de la ecuación (8) puede escribirse en función de los coeficientes de correlación, más fácilmente interpretables que las covarianzas, como: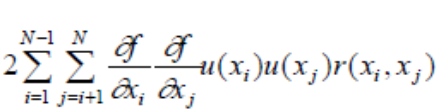 Ecuacion #11
Ecuacion #11
La ecuación (9), con ayuda de la ecuación (8), se transforma entonces en:
![]() Ecuacion #12
Ecuacion #12
De esta forma, la incertidumbre típica combinada uc(y) es simplemente una suma lineal de términos que representan las variaciones de la estimación de salida y, generada por la incertidumbre típica u(xi) de cada estimación de entrada xi.
Finalmente la nueva expresión de la incertidumbre, que satisface la exigencia de proporcionar un intervalo se denomina incertidumbre expandida, y se representa por U. La incertidumbre expandida U se obtiene multiplicando la incertidumbre típica combinada uc(y) por un factor de cobertura k que en este estudio el valor de k es igual a 2 para un nivel de confianza de 95,45%.
 Ecuacion #13
Ecuacion #13
Descripción de método de Kragten
La estimación de la incertidumbre por aproximación numérica es un método rápido y fácil, posee la ventaja, en comparación con el método diferencial propuesto por la GUM, de necesitar únicamente los valores de las magnitudes de entrada y sus incertidumbres típicas.
El método de Kragten fue desarrollado para ser implementado en una hoja de cálculo, lo cual facilita su comprensión y aplicación, su creación es rápida si se conoce el modelo matemático del mensurando y su comprensión es sencilla, y al ser universalmente aplicable, la misma lógica puede utilizarse para diferentes mensurando.
Tabla 1. Hoja de cálculo utilizada para estimar la incertidumbre por el método de Kragten.

Si alguna de las variables estuviese correlacionada, debe añadirse el término al final de la suma cuadrada. Es decir si A y B estuviesen correlacionadas, debe adicionarse:
2 * r (A, B)* (f´A – f) * (f´B –f) al termino uc2(y).
Este método sugiere una aproximación numérica a la obtención de los coeficientes de sensibilidad de los contribuyentes de incertidumbre, evitando por este medio el cálculo de las derivadas parciales del modelo y utilizando el potencial de las plantillas de cálculo para realizar el proceso en forma estructurada.
Asumiendo que y = f(xi ,x2,...,xn) es lineal en xi o que la incertidumbre típica de cada magnitud de entrada, u(xi ), es muy pequeña en comparación con el valor de la magnitud de entrada (xi), los coeficientes de sensibilidad pueden ser aproximados de la siguiente manera:
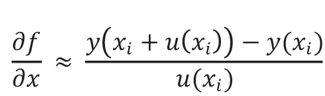 Ecuacion #14
Ecuacion #14
Finalmente la incertidumbre expandida será determinada por la ecuación 13, como se especifica a continuación:
![]()
El estadístico utilizado para realizar la comparación metrológica fue el test de HARTLEY.
En las estadísticas , la prueba de Hartley, también conocido como el Fmax de prueba o de Hartley Fmax, se utiliza en el análisis de la varianza para verificar que los diferentes grupos tienen una varianza equivalente, un supuesto necesario para otras pruebas estadísticas.
La prueba consiste en el cálculo de la relación de la mayor varianza grupo, max (sj2) a la varianza grupo más pequeño, min (sj2). La relación resultante, Fmax, a continuación, se compara con un valor crítico de una tabla de la distribución de muestreo de Fmax. Si la relación calculada es menor que el valor crítico, los grupos se supone que tienen variaciones similares o iguales.
Prueba de Hartley asume que los datos de cada grupo se distribuyen normalmente , y que cada grupo tiene un número igual de miembros. Esta prueba, aunque es conveniente, es muy sensible a violaciones de la hipótesis de normalidad.
Si la hipótesis nula es axiomática, la distribución muestral del estadístico FMax(asumiendo independencia de las muestras aleatorias tomadas de las poblaciones normales) es FMAX con t grados de libertad en el numerador y v = r − 1 grados de libertad en el denominador.
El modelo matemático utilizado en este estadístico y el criterio de aceptación son los siguientes:
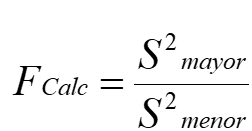 Ecuacion #15
Ecuacion #15
Criterio de aceptación:
Ho: Fcal < Ftab las varianzas son homogéneas
Tabla 2. Valores críticos de la distribución Fmax
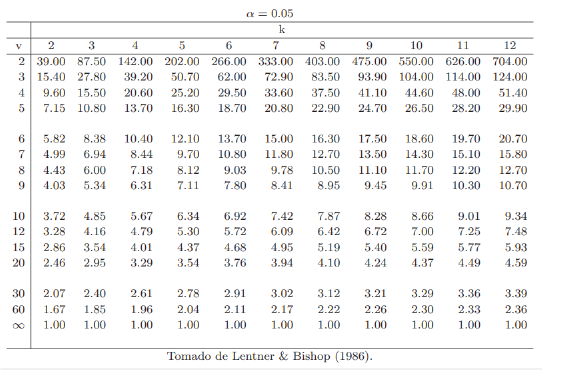
RESULTADOS Y DISCUCIONES
Los resultados obtenidos aplicando la ecuación #1 en la determinación de dureza total se presentan en la tabla 3.
Tabla 3. Resultados obtenidos en la determinación de Dureza total en mg/kg como CaC03.
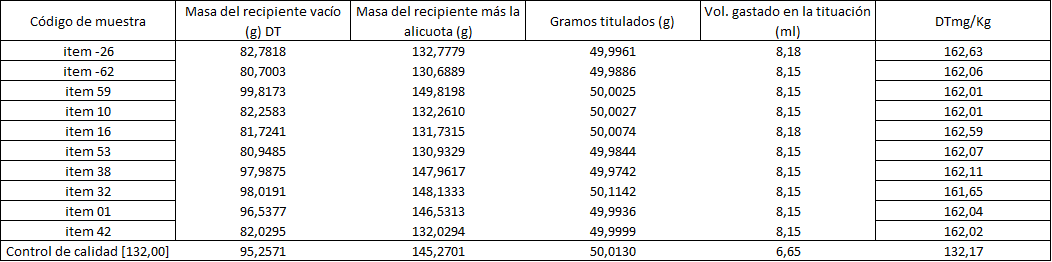
Como control de calidad de se utilizó un Material de referencia preparada en el laboratorio con una concentración de 132,00 mg.l-1 como CaC03.
Los diferentes ítems utilizados fueron previamente elaborados en el laboratorio con una concentración teórica de 162,00mg/kg de dureza total como CaC03 y posteriormente codificados de forma aleatoria utilizando el software de Excel.
Resultado obtenido al aplicar la técnica GUM para estimar la incertidumbre de medición.
A partir del modelo matemático (ecuación 1), se definieron los coeficientes de sensibilidad por derivación parcial como se observa en la tabla 4.
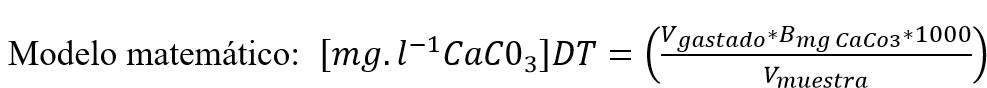
Tabla 4. Coeficientes de sensibilidad.
| Coeficientes de sensibilidad e incertidumbres | Modelación matemática |
| Coeficiente de sensibilidad con respecto a V.gastado | 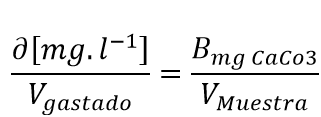 |
| Coeficiente de sensibilidad con respecto a V.muestra | 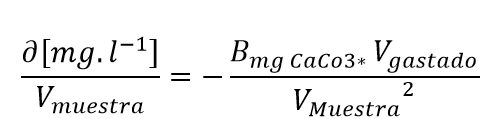 |
| Coeficiente de sensibilidad con respecto a B mg CaC03 | 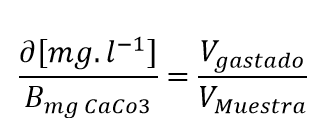 |
| Incertidumbre debido a MM Ca | 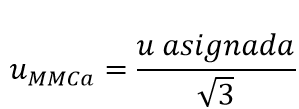 |
| Incertidumbre debido a MM CaC03 | 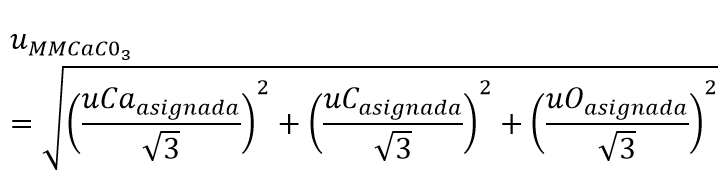 |
| Incertidumbre debido a la estandarización B | 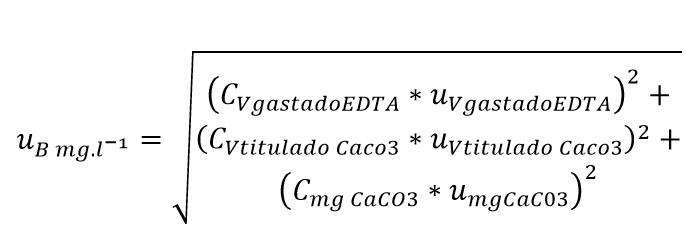 |
Ley de propagación de las incertidumbres por GUM:
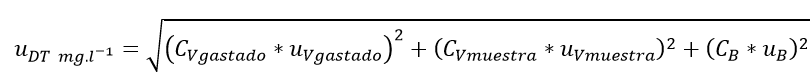
Donde:
![]() Coeficiente de sensibilidad debido al volumen gastado en la titulación.
Coeficiente de sensibilidad debido al volumen gastado en la titulación.
![]() Incertidumbre debido al volumen gastado en la titulación
Incertidumbre debido al volumen gastado en la titulación
![]() Coeficiente de sensibilidad debido al volumen la muestra.
Coeficiente de sensibilidad debido al volumen la muestra.
![]() Incertidumbre debido al volumen la muestra.
Incertidumbre debido al volumen la muestra.
![]() Coeficiente de sensibilidad de la estandarización del CaC03
Coeficiente de sensibilidad de la estandarización del CaC03
![]() Incertidumbre típica debido a la estandarización del CaC03
Incertidumbre típica debido a la estandarización del CaC03
En la tabla 5 se observan los resultados obtenidos aplicando la ley de propagación de la incertidumbre por GUM.
Tabla 5. Resultados obtenidos de la estimación de la incertidumbre por GUM.
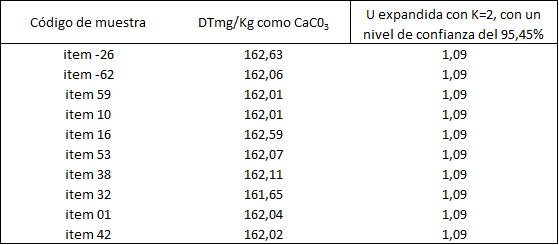
Las incertidumbres expandidas se reportaron con dos cifras significativas al igual que se reporta en mensurando con las mismas unidades de medidas (mg/kg como CaC03). Los cálculos de coeficientes de sensibilidad y estimaciones de incertidumbre por GUM se realizaron para cada uno de los ítems en estudio.
Partiendo de la ecuación general para la determinación de Dureza total y la técnica de Kragten se obtiene como resultado:
Tabla 6. Proceso para la obtención de los resultados obtenidos de la estimación de la incertidumbre por Kragten.
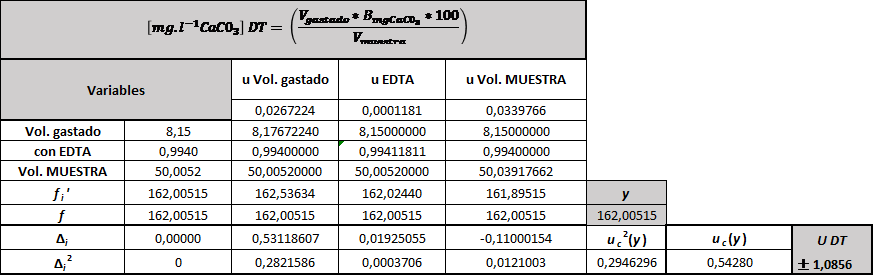
Los resultados obtenidos por la técnica de KRAGTEN se muestras por medio de la tabla 7.
Tabla 7. Resultados obtenidos de la estimación de la incertidumbre por Kragten.
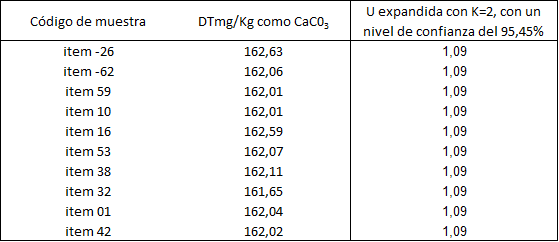
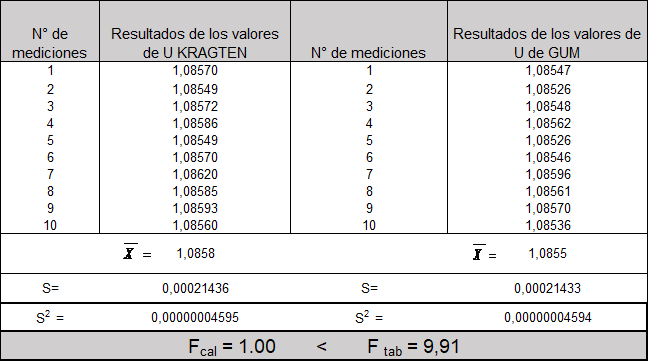
Resultados obtenidos al aplicar el test Fmax se expresan en la Tabla 8.
Al aplicar el test de Fmax se tomaron en cuenta el número de mediciones individuales realizadas durante el análisis al igual que un ![]() del 0,05.
del 0,05.
DISCUCIÓN
Para la estimación de la incertidumbre asociada al mensurando en cuestión, los métodos de la guía GUM y la guía EURACHEM (Método de la hoja de cálculo de Kragten para la estimación de la incertidumbre) resultan ser técnicas apropiadas para la asignación de una deviación asociada a la medición.
Dentro de los resultados se observan que las incertidumbres fueron evaluadas a partir de 5 cifras significativas a partir del punto, esto con el objetivo de observar estadísticamente la variabilidad entre una estimación y otra.
Al aplicar el test estadístico de Fmax y observar que los resultados para el Fcal son menores que el FTab. Por lo que se acepta la hipótesis de homogeneidad entre varianzas y por lo tanto las varianzas entre una técnica y otra no son significativas.
CONCLUCIONES
Las técnicas metrológicas de GUM y Kragten resultaron ser adecuadas para ser utilizadas en la estimación de la incertidumbre de las mediciones de dureza total por el método titrimétrico del ácido etilendiamino tetraacético (EDTA) en agua potable y natural descrito en el Standard Methods for the examination of water and wastewater. (2012). 22nd. Edition. Washington: APHA con código 2340.C.
El estadístico aplicado para la evaluación de las técnicas metrológicas es adecuado ya que se pudo observar el comportamiento numérico de las mediciones y la variabilidad entre los grupos de mediciones.
En la comparación metrológica de la metodología de determinación de DT en agua potable, para los métodos de GUM Y Kragten resultaron incertidumbres de ± 1.0855 y ± 1.0858 respectivamente, dichos valores basándose en el uso de probabilidades para expresar cuantitativamente la incertidumbre, no son significativamente diferentes por lo que ambos casos son válidos para garantizar la uniformidad y exactitud requerida de los resultados.
Al aplicar el test estadístico de Fmax, y observar que los resultados para el Fcal (1,00) son menores que el FTab. (9,91). Por lo que se concluye que la homogeneidad entre varianzas para las técnicas de GUN y Kragten no son significativas, lo que indica, desde el punto de vista estadístico, que ambas técnicas pueden ser utilizadas para estimar la incertidumbre de la medición.
REFERENCIAS
Standard Methods for the examination of water and wastewater. (2012). n. Washington: APHA. 22nd. Edition.
EURACHEM/CITAC .2012. Guide Quantifying Uncertainty in Analytical Measurement QUAM: 2012.P1. Third Edition, Editors S L R Ellison (LGC, UK) A Williams (UK).
Centro Español de Metrología. 2008. Evaluación de datos de medición — Guía para la expresión de la incertidumbre de medida. España. EDICIÓN DIGITAL 1 en español (traducción 1ª Ed. Sept. 2008) Primera Edición Septiembre 2008 (original en inglés).
Centro Español de metrología. JCGM 101: 2008. Evaluación de datos de medición—Suplemento 1 de la “Guía para la expresión de la incertidumbre de medida”—Propagación de distribuciones aplicando el método de Monte Carlo. España. Primera edición, 2008. Primera edición de la traducción al español, 2010.
Kragten, J. (1994). Calculating standard deviations and confidence intervals with a universally applicable spreadsheet technique. Analyst, 119, 2161 - 2165.
Centro español de Metrología. 2012. Vocabulario Internacional de Metrología Conceptos fundamentales y generales, y términos asociados (VIM). España. 3ª Edición en español 2012 Traducción de la 3ª edición del VIM 2008, con inclusión de pequeñas correcciones.
© 2020 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
