Estudio del potencial eólico en el municipio de San Nicolás, Estelí. Nicaragua
Study of wind potential in the municipality of San Nicolás, Estelí. Nicaragua
Juan Alberto Betanco Maradiaga
juan.betanco@yahoo.com
Emilio Pérez Castellón
emiliopc21@hotmail.com
Recibido: 31 de mayo de 2019, Aceptado: 01 de julio de 2019
1 Docente titular Universidad Nacional Autónoma de Nicaragua, FAREM-Estelíar al título de licenciatura en administración de empresas en el año 2019, por UNAN – Managua, FAREM – Estelí.
2 Dr. Profesor Universidad Nacional Agraria. Tutor científico doctorado en Gestio y Calidad de la Investigación Científica.
RESUMEN
Se evaluó el potencial del recurso eólico, analizando datos registrados por estaciones situadas en las comunidades del municipio de San Nicolás, La Laguna y El Sesteo, a la altura de 10 metros sobre el nivel del terreno, durante 40 meses de los años 2012, 2013, 2014, 2017 y 2018; sobre velocidad del viento, dirección del viento, humedad, temperatura y presión. A partir de estos datos se han construido curvas de velocidades del viento, perfil del viento, rosas de viento y perfil de potencias. Se comprobaron correlaciones significativas entre factores como altitud, velocidad, temperatura, humedad, presión, dirección y densidad del aire, mediante correlación de Pearson. Se demostraron relaciones de causalidad mediante ANOVA unifactorial entre: sitio sobre temperatura, velocidad y potencia disponible, dirección del viento sobre temperatura y velocidad del viento, entre otras. Mediante ANOVA bifactorial se demostró el efecto simultáneo de los factores sitio-velocidad, sitio-dirección del viento sobre potencia energética disponible y mediante ANACORR se demuestro una fuerte asociación positiva entre las variables velocidad del viento y potencia disponible. Se concluye que San Nicolás dispone de condiciones favorables del recurso eólico, con una velocidad media del viento 11.19 m/s, con vientos que prevalecen del Este Noreste, con potencial para generar energía.
Palabras claves: recursos eólicos; velocidad del viento; dirección del viento; potencia disponible; ANOVA.
ABSTRACT
The potential of the wind resource was assessed, analyzing data recorded by stations located in the communities of the municipality of San Nicolás, La Laguna and El Sesteo, at the height of 10 meters above ground level, for 40 months of the years 2012, 2013, 2014 , 2017 and 2018; wind speed, wind direction, humidity, temperature and pressure. From this data have been built curves of wind speeds, wind profile, wind roses and power profile. Significant correlations were checked between factors such as altitude, speed, temperature, humidity, pressure, direction and air density, using Pearson correlation. Causality ratios were demonstrated through single-factor ANOVA between: site over temperature, speed and available power, wind direction over wind temperature and wind speed, among others. The simultaneous effect of the site-speed, site-direction of wind factors on available energy power was demonstrated by ANACORR and anANACORR demonstrated a strong positive association between the wind speed and power available. It is concluded that San Nicolás has favorable conditions of the wind resort, with an average wind speed of 11.19 m/s, with winds prevailing from the Northeast, with the potential to generate energy.
Keywords: wind resources; wind speed; wind direction; available power; ANOVA.
INTRODUCCIÓN
En Nicaragua han ocurrido significativos avances en el uso de energías renovables alcanzando un 53 %; sin embargo, aún se utiliza un 47 % de energía dependiente de combustible fósil, así mismo se ha logrado que un 90 % de la población tenga acceso a la energía eléctrica; hay que hacer esfuerzos en conjunto academia – estado, para disminuir el 10 % de habitantes que aún no tienen acceso (ENATREL, 2016).
Según el Instituto Nacional de Información de Desarrollo INIDE (2008), “el municipio de San Nicolás, cuenta con 1409 viviendas. Los habitantes presentan un índice alto de pobreza extrema de 57,9 % y pobreza no extrema de 30,1 %”. El municipio cuenta con un capital natural importante que manejado justo y equitativamente, puede aprovecharse para contribuir al desarrollo humano sostenible de los miembros de la comunidad. El viento que posee el municipio necesita evaluarse para medir su potencial de generación de energía renovable y realizar un apropuesta técnica que fomenta el desarrollo socio económico. En julio del 2016, ENATREL reporta que San Nicolás, posee un 70 por ciento de electrificación en su territorio.
El propópsito del presente estudio es contribuir con la evaluación del potencial del recursos energéticos, en función de los parámetros del recurso viento en el municipio de San Nicolás. Así mismo con los datos recopilados establecer las correlaciones entre los factores del recuros y las relaciones de causalidad entre los parámetros del recurso viento y la potencia energética.
Estudios similares se han realizado a nivel internacional. La división de investigación y desarrollo tecnológico del instituto tecnológico de Canarias (Rodríguez, 2010, pág. 23), desarrolló un estudio sobre evaluación del potencial eólico máximo instalable en la isla de Gran Canaria, calculando el potencial eólico máximo posible en unos 590 MW con una producción de energía anual de 1.600 GWh aproximada. Hernández Escobedo, Espinoza Arenal, Saldaña Flores y Rivera Blanco (2012, pág. 215), realizaron un estudio con el objetivo de evaluar el recurso eólico, para su posible utilización en la generación de energía eléctrica en el Estado de Veracruz, México. Se encontró que existen regiones con velocidad promedio del viento de 5.45 m/s, valor que se ajusta para producir energía eléctrica aproximada de 14,432 kW.
En Venezuela, Rigoberto Andressen L. y Carlos La Rosa (2012, pág. 84), realizaron evaluación meteorológica del aprovechamiento eólico. En este trabajo, a partir de los datos de vientos obtenidos en 30 estaciones meteorológicas distribuidas en el territorio nacional, se hace una evaluación preliminar de la potencia eólica estimada. Se concluye que los lugares con alta potencialidad para generación de energía eólica, se encuentran en la Isla de Margarita, la Guajira y en localidades insulares. Mediana potencialidad encontró la península de Paraguaná. El resto del país, no presenta buenas perspectivas para generación de energía eólica.
Los estudios citados tienen un objetivo común con la presente investigación ya que se indaga mediante experimentación natural sobre la velocidad del viento de una zona determinada, los factores climáticos que inciden y su potencial eólico disponible para la producción de energía eléctrica en la localidad específica.
MATERIALES Y MÉTODOS
Tipo de Estudio
De acuerdo al método de investigación el presente estudio es experimental (Pedroza, 1993). De acuerdo a la clasificación de Hernández, Fernández y Baptista (2014), el tipo de estudio es correlacional. De acuerdo, al tiempo de ocurrencia de los hechos y registro de la información, el estudio es prospectivo, por el período y secuencia del estudio es longitudinal y según el análisis y alcance de los resultados el estudio es analítico (Canales, Alvarado, & Pineda, 1994).
Área de estudio
El área geográfica se enfoca en Las Segovias de Nicaragua, específicamente en el Municipio de San Nicolás que cuenta con tres barrios, 10 microrregiones y está ubicado en la posición geográfica con latitud: 12.9333 y longitud: -86.3333. Las comunidad San José de Laguna se encuentra en la coordenadas latitud 12.9628, y longitud -86,3419 a un altura de 1355 msnm y la comunidad El Sesteo en la latitud 12.9517, longitud -86.3411 y altitud 1323 msnm.
Universo y muestra
La evaluación del potencial eólico requiere de un conocimiento exhaustivo del comportamiento del viento, cuyos parámetros obedecen a factores ambientales que ocurren en la naturaleza. El estudio de este tipo de perturbaciones que ocurren en el campo se conoce como experimentos de la naturaleza en el que las variables independientes no se pueden controlar (Diamond, 1986).
Métodos técnicas e instrumentos de recolección de datos
Con relación a la evaluación de los potenciales de los recursos energéticos, en función de los parámetros del recurso viento en el municipio de San Nicolás. El experimento se centró en el estudio de la variable no controlada, viento, en su ambiente natural en comunidades de San Nicolás. Se establecieron dos sitios experimentales con un punto de control en cada sitio. En cada sitio de control se establecieron las unidades experimentales que son estaciones meteorológicas a 10 metros de altura, equipadas con sensores como anemómetros, veletas, barómetros programados para registrar datos cada 10 minutos. Las estaciones son: combined wind transmiter y PCE-FWS 20.
Los datos de viento obtenidos se trataron estadísticamente, con el fin de obtener la distribución por rumbos de las direcciones y la distribución por frecuencias de las velocidades, las medias de la velocidad del viento, medias de la velocidad cúbica, presión y temperatura medias. La distribución de direcciones se representó por la de la rosa de los vientos, en la que se expresó el porcentaje de tiempo en el que el viento tiene una determinada dirección, la distribución de velocidades de viento para cada intervalo direccional. Para el cálculo de la densidad de potencia, se utilizó la distribución de Weibull. Se hicieron las pruebas estadísticas de correlación y de causalidad entre las variables.
Procedimientos para la Recolección de datos e información
Los datos para la medición del viento se obtuvieron mediante anemómetros, veletas, barómetros, termómetro, que se colocaron en dos sitios de la zona de San Nicolás; San José de La Laguna en casa del Sr. Eduardo López y en El Sesteo en finca Rancho de Luis del Sr. José Luis López. Los instrumentos fueron colocados en lugares expuestos a todas las direcciones y sin obstáculos en su entorno que puedan crear turbulencias. Las medidas se realizaron a la altura normalizada de lectura de 10 metros sobre el nivel del suelo. Se midió durante 40 meses correspondientes a periodos de medición en los años 2012, 2013, 2014, 2017 y 2018.
Los datos que provienen de los instrumentos de medida se registraron en data logger y mensual se transfirieron a un sistema de registro electrónico en una computadora personal. Finalmente, los registros fueron almacenados en bases de datos utilizando el software estadístico Infostat.
Plan de Tabulación y Análisis de datos e información
Se realizaron análisis paramétricos mediante la prueba de correlación de Pearson y los análisis inferenciales específicos o prueba de hipótesis, mediante análisis de varianza univariado unifactorial y Bifactorial (ANOVA de Fisher) y el test de Fisher (prueba de LSD). Asimismo, se realizó para las variables pertinentes el Análisis de Correlación Pearson (ANACORR). Los análisis inferenciales antes descritos, se realizaron utilizando el software estadístico Infostat v 2016 para Windows, de acuerdo a los procedimientos estadísticos descritos en Pedroza y Dicoskiy, (2006).
RESULTADOS Y DISCUSIÓN
Velocidad del viento
La velocidad del viento medida en San José de La Laguna y El Sesteo a 10 m de altura, presenta una media de 11.19 m/s y una mediana de 10.89 m. Velocidades del viento mínimas de calma y máximas de 33 m/s (tabla 1).
| Tabla 1. Medidas resumen variable velocidad del viento | ||||||||
| Variable | n | Media | D.E. | Var(n-1) | Min | Máx | Mediana | Kurtosis |
| Vel del Viento10m | 236909 | 11.19 | 6.36 | 40.43 | 0.00 | 32.88 | 10.89 | -0.73 |
Series Temporales de Velocidad y Dirección del Viento durante el período de mediciones
Distribución de frecuencias de velocidad del viento
Las mediciones han permitido determinar la cantidad de horas que ha permanecido el viento a determinada velocidad. Se observa en el histograma de distribución de frecuencias de las velocidades de viento, que destacan 1817 horas en velocidades de 12 a 13 m/s. Se registraron 1037 horas de calma y las velocidades de viento entre 4 m/s y 20 m/s presentaron más de 1000 para cada categoría (figura 1).
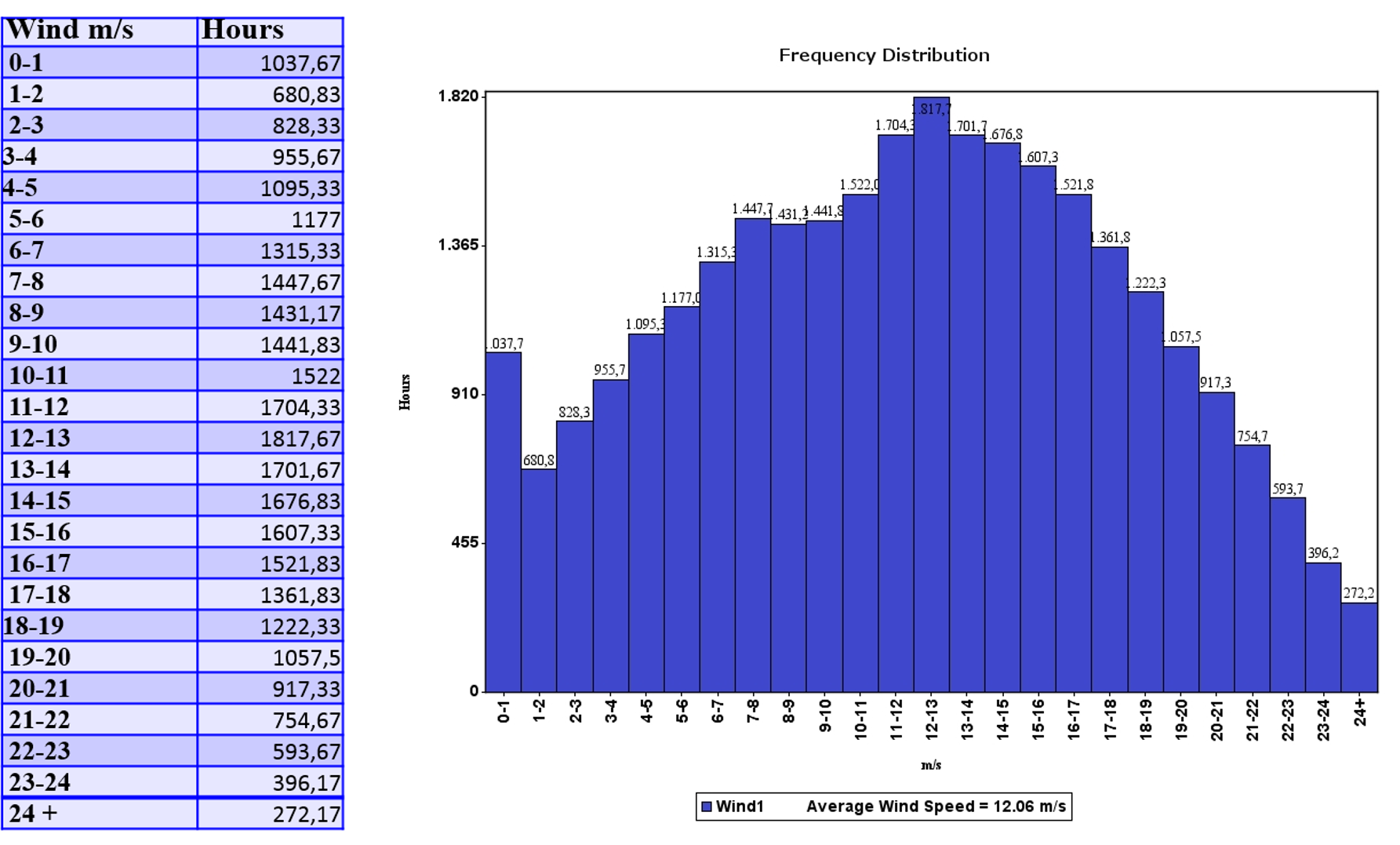
Figura 1. Distribución de frecuencias velocidad del viento en horas acumuladas, durante el período de estudio. Fuente propia.
Distribución Diurna (día y noche) de la Velocidad del Viento
Las mediciones realizadas durante los 40 meses permitieron conocer la distribución diurna de la velocidad del viento en el municipio de San Nicolás. El viento sopla más fuerte durante el día hasta medias de 13.8 m/s y baja por la noche hasta 11.3 m/s (figura 2).
Se obtuvieron velocidades de viento durante la noche de 11.3 m/s desde las 6 de la tarde, hasta 12.39 m/s a las 5 am. Durante el día aparecieron velocidades de viento de 12.61 m/s desde las 6 am hasta 10.97 m/s a las 5 pm lo cual se fundamenta en la primera ley de la termodinámica (Juliuos Mayer, 1842) en su forma adiabática que tiene que ver con las diferencias de temperatura y en el proceso de convección.
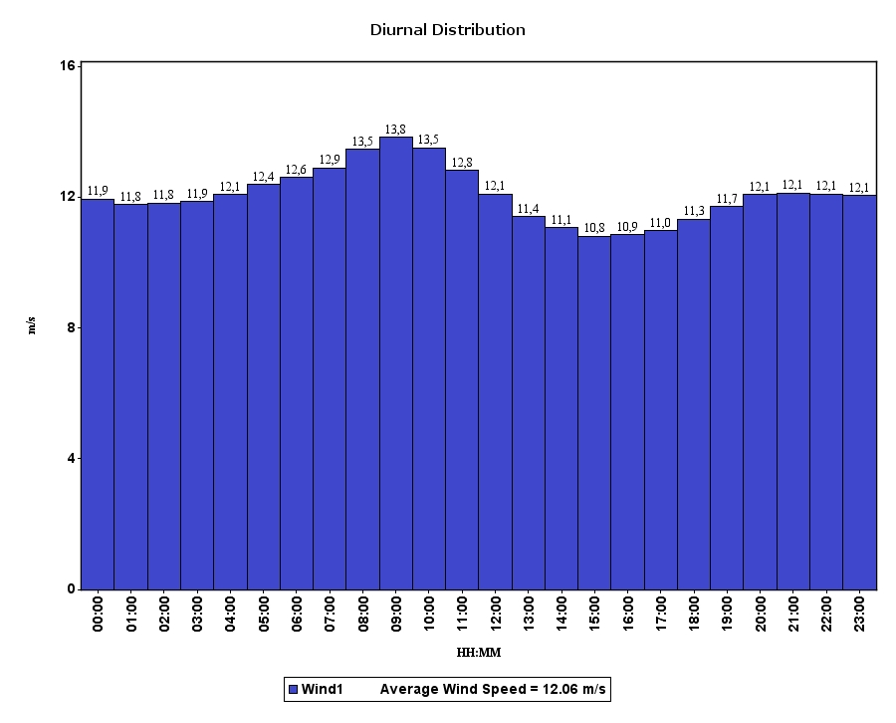
Figura 2. Distribución diurna de la velocidad del viento, durante el período de estudio.
Series temporales de velocidad anual
De abril a diciembre del 2012, se obtuvieron velocidades promedio de 10.15 m/s. Las velocidades entre 7 y 9 m/s, alcanzaron mayor cantidad de horas con 398. Las horas de calma (0-1 m/s) fueron 277.
En el año 2013 el promedio de velocidad del viento fue de 11.6 m/s. las velocidades mayores se produjeron en el intervalo 11-12 m/s, durante 509 horas. En este año se registraron 440 horas de calma.
En el año 2014 se registraron velocidades promedio de 12.95 m/s. las mayores velocidades se alcanzaron en el intérvalo de 14 a 15 m/s, alcanzand 590 horas. Las horas de calma registradas fueron 209.
En el 2017, se midió para el mes de diciembre velocidad media de 14.88 m/s. Las mayores velocidades alcanzadas fueron en el rango de 16 a 17 m/s durante 65.7 horas. En este mes se registraron 10 horas de calma.
De enero a julio 2018 la media de la velocidad del viento es de 13. 35 m/s, alcanzando durante 371 horas velocidades de 12 a 13 m/s. También se registraron 119 horas para velocidades de 6 a 7 m/s. Se registraron 102 horas de calma en este período.
Dirección del Viento Predominante 2012-2014, 2017-2018
Para el período de mediciones se observa que la dirección del viento prevaleciente es la proveniente del Este Noreste ENE (67. 50º) con 927.98 horas reflejadas en la parte radial de la gráfica. En segundo lugar, se observa también que la dirección del viento es del NNW Norte Noroeste (337.50º) durante 837.55 horas (figura 3).
Esto coincide con lo que plantea el geólogo Tupak Ernesto Obando Rivera (2009) que, Nicaragua se ve influenciada durante la mayor parte del año por los vientos alisios provenientes de anticiclones subtropicales de los Azores y Bermudas, bajo la acción del movimiento del aire desde alta presión a baja presión, la fuerza de gradiente y la fuerza de Coriolis (1836).
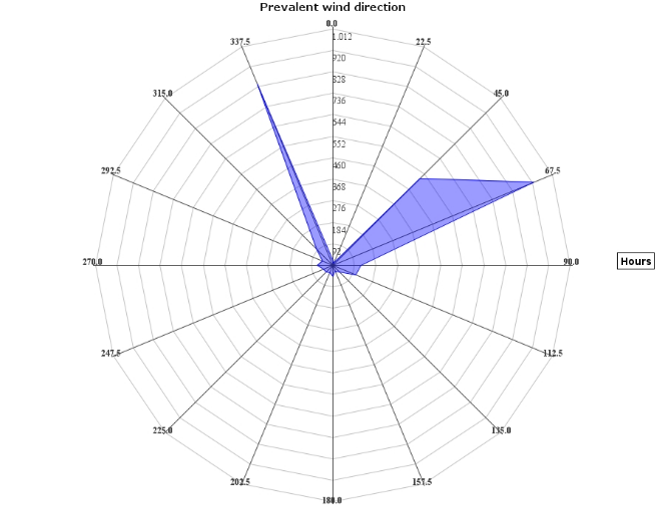
Figura 3. Dirección del viento predominante durante el periodo de medición.
Esto coincide con lo que plantea el geólogo Tupak Ernesto Obando Rivera (2009) que, Nicaragua se ve influenciada durante la mayor parte del año por los vientos alisios provenientes de anticiclones subtropicales de los Azores y Bermudas, bajo la acción del movimiento del aire desde alta presión a baja presión, la fuerza de gradiente y la fuerza de Coriolis (1836).
Dirección media de la velocidad del viento periodo 2012-2014, 2017-2018
En la rosa de los vientos de distribución de velocidad, obtenida con los datos durante el período de medición predominan los vientos del Noreste NE (45 º) - Este Noreste ENE (67.50 º), con velocidades de viento que alcanzan entre los 13,94 m/s y 14.04 m/s y del Norte Noroeste con velocidades que alcanzan 11,9 m/s (figura 4).
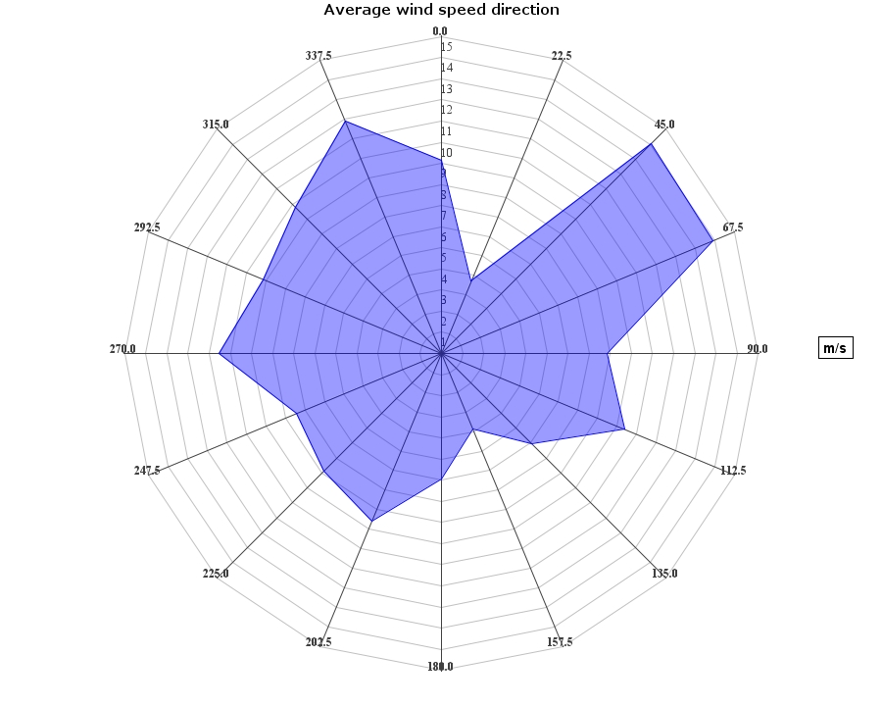
Figura 4. Dirección del viento predominante. En áreas radiales velocidad del viento. Periodo 2012-2014, 2017- 2018
Cálculo de la densidad del viento
El cálculo exacto de la densidad del aire se realizó mediante la calculadora de densidad del aire. Se introdujeron datos medidos en San José de la Laguna y El Sesteo sobre la presión del aire 863 hPa, la temperatura y la humedad para una altura de 1324 msnm. Se obtuvo como resultado una densidad del aire de 1.086 kg/m3 para la zona de San Nicolás.
Mediante el método logarítmico se elaboró el perfil de altura, en el que se observa el incremento de la velocidad del viento con el aumento de la altura (figura 5).
| Altura [m] | Velocidad del viento [m/s] |
| 150 | 19,22 |
| 140 | 18,95 |
| 130 | 18,67 |
| 120 | 18,38 |
| 110 | 18,06 |
| 100 | 17,72 |
| 90 | 17,35 |
| 80 | 16,95 |
| 70 | 16,50 |
| 60 | 16,00 |
| 50 | 15,42 |
| 40 | 14,76 |
| 30 | 13,93 |
| 20 | 12,92 |
| 10 | 11,18 |
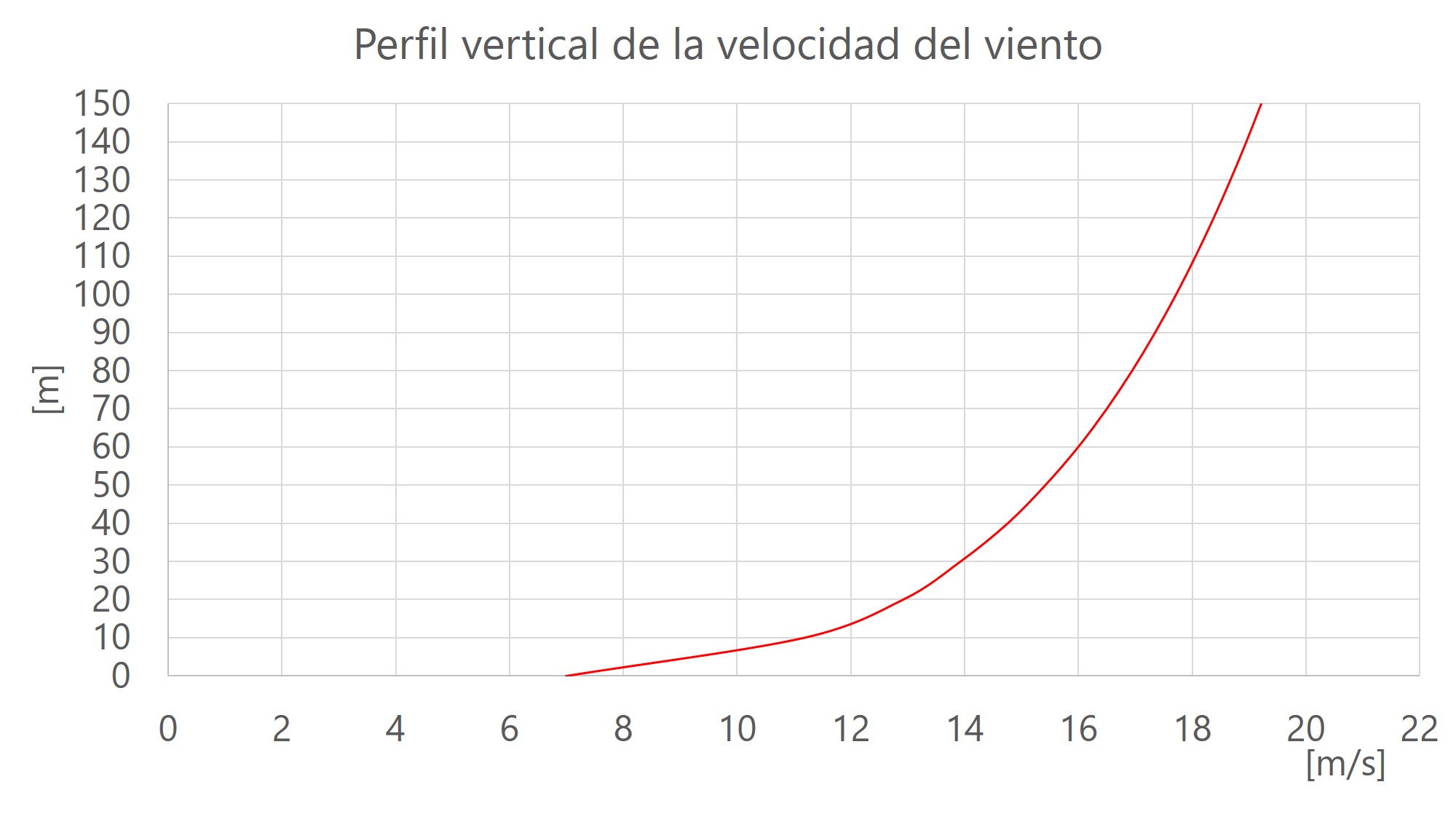
Figura 5. Perfil vertical de la velocidad del viento. Modelo logarítmico.
En la variación de los vientos superficiales (hasta 100 m de altura), influyen las fuerzas de gradiente, de Coriolis, centrifuga y de rozamiento sobre todo esta última determinada por la rugosidad de superficie. Por la teoría de la capa mínima en flujo compresible (Prandtl, 1904), el viento debido al rozamiento varía con la altura, fenómeno llamado cizalladura por lo que la velocidad del viento tiende a incrementarse a medida que se asciende y es expresado mediante fórmulas matemáticas como los modelos exponencial y logarítmico del viento.
Distribución de Weibull
Para evaluar el potencial eólico se utiliza la ley de densidad de probabilidad de Weibull que permite obtener una distribución matemática para predecir con buena aproximación, la conducta de la velocidad del viento durante un periodo de tiempo. Las distribuciones analíticas expresan la probabilidad de que la velocidad del viento tome un valor determinado.
Calculo de factor de forma y escala
Mediante regresión lineal, aplicada a la distribución de frecuencia acumulada de los datos medidos se obtuvo la recta de distribución (figura 6)
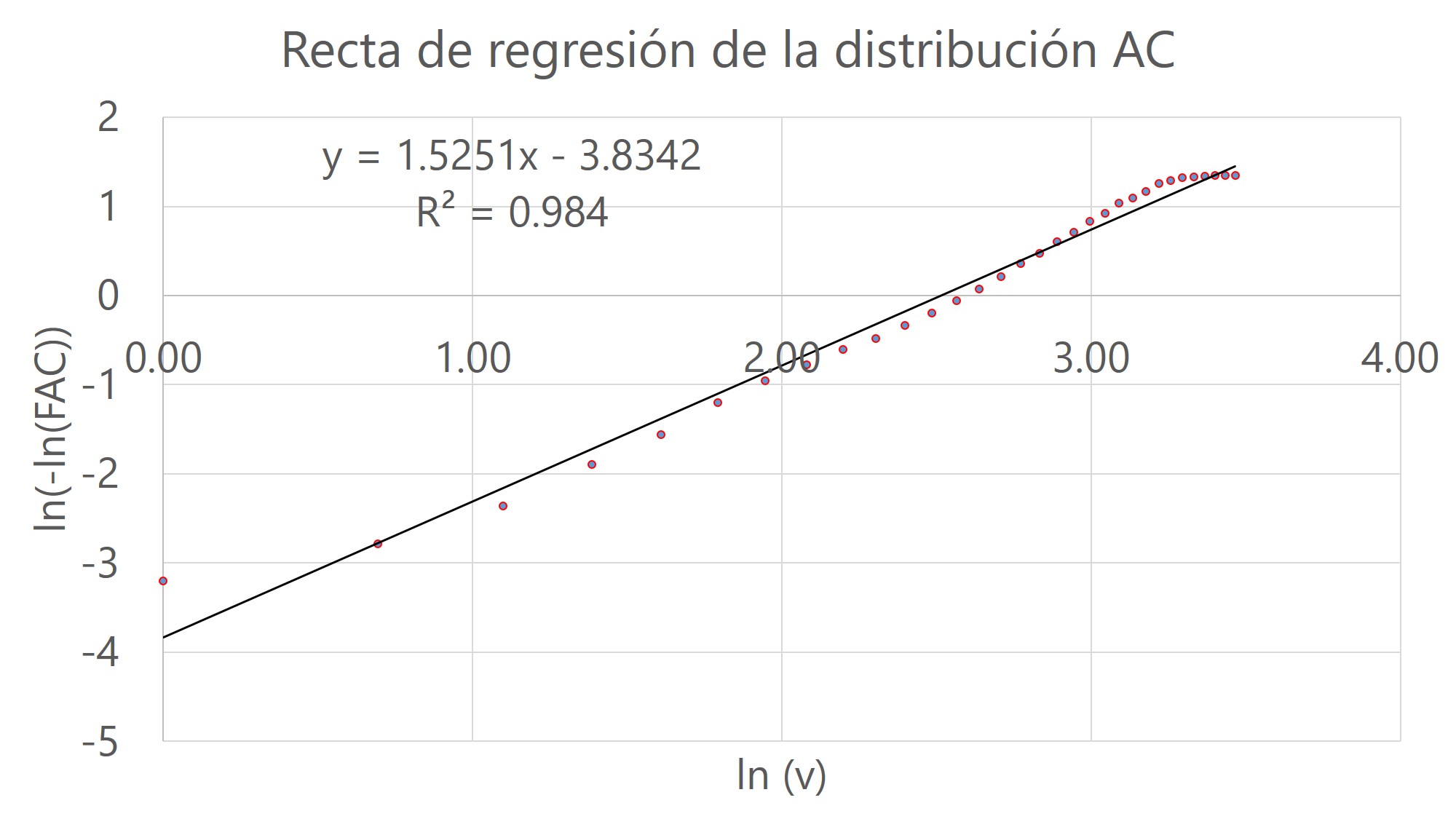
Figura 6. Recta de regresión de la distribución acumulada complementaria
La recta de regresión es:
y = 1,5251x - 3,8342
de la cual se determinó el factor de forma k y el factor de escala c.
Factor de forma, es el factor de la variable
independiente: k = 1,52 (La pendiente)
Factor de escala: c = e –(b/k) = e –(-3.8342/1.52) = 12,88 m/s
Finalmente se determina para el lugar de estudio, la denominada ecuación de Weibull.
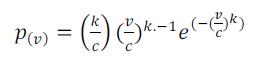
P(v) = (1,52/12,88) * (v/12,88) 1,52-1 * e (-(v/12,46) ^1,52)
Curva de Densidad de Potencia Disponible en Función de la Velocidad del Viento
La potencia eólica disponible permitió conocer la máxima potencia que se puede extraer del viento. Indica la potencia por unidad de área perpendicular al viento. El potencial eólico disponible aumenta con el cubo de la velocidad y es directamente proporcional a la densidad del aire. Se muestran la potencia disponible para 10 m de altura (figura 7).
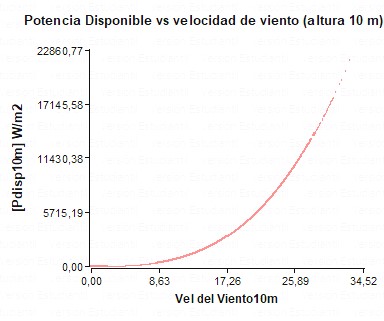
Figura 7. Curva de densidad de potencia disponible.
La potencia eólica disponible aumenta al aumentar la altura. Para altura de 10 m y velocidad media de 10 m/s, la potencia disponible es 815.24 W/m2. La potencia aumenta a 3265 W/m2, al incrementarse la altura por ejemplo a 100 m y velocidad media de 17,47 m/s (tabla 2).
| Tabla 2. Perfil de potencia disponible | ||||||||||
| Altura m. | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Velocidad del viento m/s | 11 | 12,95 | 14,09 | 14,9 | 15,53 | 16,04 | 16,47 | 16,85 | 17,18 | 17,47 |
| Potencia disponible W/m2 | 815,24 | 1330,20 | 1713,32 | 2026,12 | 2294,14 | 2527,66 | 2736,45 | 2930,26 | 3105,81 | 3265,76 |
Análisis Correlación y Asociación de los Parámetros relacionados a la Velocidad del Viento
Mediante correlación de Pearson, se comprobaron correlaciones entre: Altitud y velocidad del viento, temperatura y velocidad del viento, humedad relativa y velocidad del viento, presión y velocidad del viento, dirección y velocidad del viento, temperatura y densidad del aire y mediante el estadístico chi cuadrado de Pearson, correlación entre día/noche y velocidad del viento y entre estación (lluviosa-seca) y velocidad del viento.
Entre Altitud y Velocidad del Viento
| Tabla 3. Correlación de Pearson altitud y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Altitud msnm | altitudmsnm | 236909 | 1.00 | <0,0001 |
| Altitud msnm | Viento10m | 236909 | -0,28 | <0,0001 |
| Altitud msnm | [viento 20m] | 236909 | -0,28 | <0,0001 |
| Altitud msnm | [viento 30m] | 236909 | -0,28 | <0,0001 |
| Altitud msnm | [Viento 40m] | 236909 | -0,28 | <0,0001 |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor” que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre altitud y velocidad del viento (tabla 3).
Entre Temperatura y Velocidad del Viento
| Tabla 4. Correlación de Pearson temperatura y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Temperatura | Temperatura | 236903 | 1,00 | <0,0001 |
| Temperatura | Viento10m | 236903 | -0,15 | <0,0001 |
| Temperatura | [viento 20m] | 236903 | -0,15 | <0,0001 |
| Temperatura | [viento 30m] | 236903 | -0,15 | <0,0001 |
| Temperatura | [Viento 40m] | 236903 | -0,15 | <0,0001 |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre la temperatura y la velocidad del viento. En este contexto, la prueba de Correlación de Pearson, demuestra que la temperatura desciende con el aumento de la velocidad del viento (tabla 4).
Entre Humedad Relativa y Velocidad del Viento
| Tabla 5 Correlación de Pearson humedad relativa y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Humedad | Humedad. | 49892 | 1,00 | <0,0001 |
| Humedad | Velocidad del viento | 49892 | -0,30 | <0,0001 |
| Velocidad del viento | Humedad | 49892 | -0,30 | <0,0001 |
| Velocidad del viento | Velocidad del viento | 49986 | 1,00 | <0,0001 |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor” que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre la humedad y la velocidad del viento (tabla 5).
Entre Presión y Velocidad del Viento
| Tabla 6. Correlación de Pearson presión absoluta y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Presión Absoluta [hPa] |
Presión Absoluta [hPa] |
49986 | 1,00 | <0,0001 |
| Presión Absoluta [hPa] |
Velocidad del viento | 49986 | -0,08 | <0,0001 |
| Velocidad del viento | Presión Absoluta [hPa] |
49986 | -0,08 | <0,0001 |
| Velocidad del viento | Velocidad del viento | 49986 | 1,00 | <0,0001 |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor” que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre la presión absoluta y la velocidad del viento (tabla 6).
Entre Dirección y Velocidad del Viento
| Tabla 7. Correlación de Pearson dirección de viento y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Dirección | Dirección. | 236909 | 1,00 | <0,0001 |
| Dirección | Vel del Viento10m | 236909 | 0,03 | <0,0001 |
| Vel del Viento10m | Dirección | 236909 | 0,03 | <0,0001 |
| Vel del Viento10m | Vel del Viento10m | 236909 | 1,00 | <0,0001 |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor” que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre la dirección del viento y velocidad del viento (tabla 7).
Entre Temperatura y Densidad del Aire
| Tabla 8. Correlación de Pearson dirección de viento y velocidad del viento | ||||
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Densidad viento | Densidad viento | 236903 | 1,00 | <0,0001 |
| Densidad viento | Temperatura | 236903 | -1,00 | <0,0001 |
| Temperatura | Densidad viento | 236903 | -1,00 | <0,0001 |
| Temperatura | Temperatura | 236903 | 1,00 | |
La prueba de Correlación de Pearson aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es “menor” que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, la prueba de Correlación de Pearson, demostró que existe una correlación significativa entre temperatura y densidad del viento (tabla 8).
Entre Día/Noche y Velocidad del Viento
Tabla 9. Análisis de contingencia chi cuadrado Pearson entre día/noche y velocidad del viento
| Frecuencias absolutas. En columnas: horario | |||
| Beafourt | Día | Noche | Total |
| Brisa débil (3.4-5.4) | 13830 | 13054 | 26884 |
| Brisa fresca (8.0-10.7)15516 | 15516 | 14572 | 30088 |
| Brisa fuerte (10.8-13.8) 17579 | 17579 | 18331 | 35910 |
| Brisa moderada (5.5-7.9) 17535 | 17535 | 17228 | 34763 |
| Brisa muy débil | 6947 | 6379 | 13326 |
| Calma (0.0-0.2) | 2083 | 3418 | 5501 |
| Temporal | 14340 | 14506 | 28846 |
| Temporal duro | 2147 | 1593 | 3740 |
| Temporal fuerte | 7621 | 7030 | 14651 |
| Temporal huracanado | 136 | 526 | 392 |
| Temporal muy duro | 261 | 245 | 506 |
| Ventolina | 2590 | 3488 | 6078 |
| Viento fuerte | 17838 | 18386 | 36224 |
| Total | 118423 | 118486 | 236909 |
| Estadiístico | Valor | p |
| Chi Cuadrado Pearson | 709,72 | <0,0001 |
| Chi Cuadrado MV-G2 | 708,38 | <0,0001 |
Como el valor p = 0,0001 es menor que el nivel de significancia α= 0,05, se rechaza la hipótesis nula y se concluye, según la prueba de Chi Cuadrado, que hay una asociación estadísticamente significativa entre las variables velocidad del viento y horario: día y noche (tabla 9).
Entre Estación (Lluviosa-Seca) y Velocidad del Viento (Escala Beaufort)
Tabla 10 Análisis de contingencia chi cuadrado Pearson entre la Estación (Lluviosa-Seca) y velocidad del viento
Frecuencias relativas al total (expresadas como porcentajes). En columnas: Estación
| Beaufort | LLUVIOSA | SECA | Total |
| Brisa débil | 6,41 | 4,94 | 11,35 |
| Brisa fresca | 6,72 | 5,98 | 12,70 |
| Brisa fuerte | 7,85 | 7,30 | 15,16 |
| Brisa moderada | 7,44 | 7,23 | 14,67 |
| Brisa muy débil | 3,79 | 1,83 | 5,62 |
| Calma | 1,40 | 0,92 | 2,32 |
| Temporal | 5,36 | 6,81 | 12,18 |
| Temporal duro | 0,82 | 0,76 | 1,58 |
| Temporal fuerte | 2,74 | 3,44 | 6,18 |
| Temporal huracanado | 0,16 | 3,0E-03 | 0,17 |
| Temporal muy duro | 0,11 | 0,10 | 0,21 |
| Ventolina | 1,85 | 0,72 | 2,57 |
| Viento fuerte | 7,75 | 7,54 | 15,29 |
| Total | 52,42 | 47,58 | 100,00 |
| Estadiístico | Valor | p |
| Chi Cuadrado Pearson | 4077,29 | <0,0001 |
| Chi Cuadrado MV-G2 | 4256,42 | <0,0001 |
Como el valor p = 0,0001 es menor que el nivel de significancia α= 0,05; se rechaza la hipótesis nula y se concluye según la prueba de Chi Cuadrado, que hay una asociación estadísticamente significativa entre las variables velocidad del viento y estación: lluviosa y seca (tabla 10).
La velocidad del viento se relaciona con factores climáticos como la altitud, temperatura, humedad, presión y dirección del viento ya que el viento se forma cuando el aire se dirige desde las zonas de alta presión hacia las zonas de baja presión, la presión se eleva cuando sube la temperatura con la densidad es constante. Evangelista Torricelli (1643) fue el primero en explicar científicamente que, los vientos son producidos por diferencias en la temperatura del aire, y por tanto de la densidad, entre dos regiones de la tierra, lo cual coincide con las demostraciones mediante correlación de Pearson, con la que se comprobaron correlaciones de los datos recopilados en el periodo de medición entre: Altitud y velocidad del viento, temperatura y velocidad del viento, humedad relativa y velocidad del viento, presión y velocidad del viento, dirección y velocidad del viento, temperatura y densidad del aire y mediante el estadístico chi cuadrado de Pearson, correlación entre día/noche y velocidad del viento y entre estación lluviosa-seca y velocidad del viento.
Relaciones de causalidad
Se demostraron relaciones de causalidad, mediante ANOVA unifactorial entre: sitio sobre temperatura, sitio sobre velocidad del viento, sitio sobre potencia disponible, dirección del viento sobre temperatura, dirección del viento, sobre la velocidad del viento, horario (diurno/nocturno) sobre la velocidad del viento, estación sobre velocidad del viento. Mediante ANOVA bifactorial se demostró el efecto simultaneo de los factores sitio * velocidad del viento sobre potencia energética disponible y sitio * dirección del viento sobre potencia energética disponible.
Para todas las relaciones de causalidad demostradas, primeramente se comprobó que la variable real cumpliera con los principios o supuestos paramétricos: Normalidad de los residuos, homogeneidad de la varianza de los residuos (prueba de Levenne) e independencia de los residuos.
Relación de Causalidad entre el Sitio y la Temperatura
Tabla 11. ANOVA SITIO (causa), sobre la temperatura
Análisis de la varianza
| Variable | N | R2 | R2 AJ | CV |
| Temperatura | 231252 | 0,01 | 0,01 | 20,90 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 46365,39 | 1 | 46365,39 | 2778,44 | <0,0001 |
| Sitio | 46365,39 | 1 | 46365,39 | 2778,44 | <0,0001 |
| Error | 3858994,69 | 231250 | 16,69 | ||
| Total | 3905360,08 | 231251 |
Test: LSD Fisher Alfa=0,05 DMS=0,04048
Error: 16,6875 gl: 231250
| Sitio | Media | n | E.E. | |
| San José La Laguna | 30,39 | 49896 | 0,02 | A |
| El Seteo | 19,31 | 181356 | 0,01 | B |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza, demostró que existen diferencias significativas en la temperatura, por causa de los diferentes sitios (tabla 11).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: El sitio definido por la categoría San José de la Laguna, muestra en primer lugar, (categoría A) el efecto de una mayor temperatura (º C), con media de 20.39. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor temperatura (meses), con medias de 19.31 para el sitio definido por la categoría El Sesteo (tabla 11).
El gradiente térmico se debe a que la fuente de calor en la atmósfera es la irradiación desde el suelo; por lo tanto, mientras más alejado de la fuente, más frío estará el aire. En las zonas montañosas que atraviesa el país de Noroeste a Sureste, y modifica el clima, las temperaturas disminuyen con un gradiente vertical de 0,6 °C por cada 100 m. En algunos casos en ciertas regiones de la atmósfera la temperatura aumenta con la altura en una inversión de temperatura, en una superficie de inversión cuando el aire desciende por enfriamiento aumenta la presión y la consecuente pérdida de temperatura, esto último coincide con la demostración de causalidad mediante ANOVA del efecto del sitio sobre temperatura, en el que se demostró que existen diferencias significativas en la temperatura, por causa de los diferentes sitios San José de la Laguna y El Sesteo.
Relación de Causalidad entre el Sitio y la Velocidad del Viento
Tabla 12 ANOVA SITIO (causa), sobre la velocidad del viento Análisis de la varianza
| Variable | N | R2 | AJ | CV |
| Viento10m | 231257 | 0,07 | 0,07 | 54,88 |
Cuadro de Análisis de la Varianza
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 652053,85 | 1 | 652053,85 | 17188,54 | <0,0001 |
| Sitio | 652053,85 | 1 | 652053,85 | 17188,54 | <0,0001 |
| Error | 8772749,03 | 231255 | 37,94 | ||
| Total | 9424802,88 | 23 1256 |
Test: LSD Fisher Alfa=0,05 DMS=0,06102
Error: 37,9354 gl: 231255
| Sitio | Media | n | E.E. | |
| El Sesteo | 12,10 | 181356 | 0,01 | A |
| San José La Laguna | 8,02 | 49901 | 0,03 | B |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la velocidad del viento a 10 m de altura, por causa de los diferentes sitios (tabla 12).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: El sitio definido por la categoría El Sesteo, muestra en primer lugar, (categoría A) el efecto de una mayor velocidad del viento a 10 m (m/s), con media de 12.10 m/s. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor velocidad del viento a 10 m (m/s), con medias de 8.02 para el sitio definido por la categoría San José de La Laguna (tabla 12).
El ANOVA efecto sitio sobre velocidad del viento, demostró que existen diferencias significativas en la velocidad del viento a 10 m de altura, por causa de los diferentes sitios. El sitio definido por la categoría El Sesteo, muestra en primer lugar, (categoría A) el efecto de una mayor velocidad del viento a 10 m, con media de 12.10 m/s. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor velocidad del viento a 10 m, con medias de 8.02 m/s para el sitio definido por la categoría San José de La Laguna, lo cual coincide con el hecho de que, en la capa atmosférica superficial, la velocidad del viento tiende a incrementarse a medida que se asciende además de la influencia de vientos locales como vientos de valle y montaña generados por diferencia de presiones.
Relación de Causalidad entre Dirección del Viento y Temperatura
Tabla 13. ANOVA efecto Dirección del viento [rumbo] sobre Temperatura Análisis de la varianza
| Variable | N | R2 | R2 AJ | CV |
| Temperatura | 231078 | 0,10 | 0,10 | 20,00 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 373728,33 | 15 | 24915,22 | 1630,46 | <0,0001 |
| Dirección [rumbos] | 373728,33 | 15 | 24915,22 | 1630,46 | <0,0001 |
| Error | 3530872,41 | 231062 | 15,28 | ||
| Total | 3904600,74 | 231077 |
Test: LSD Fisher Alfa=0,05 DMS=0,18915
Error: 15,2811 gl: 231062
| Dirección [rumbos] | Medias | n | E.E. | |||||||||||
| NNW | 21,35 | 52131 | 0,02 | A | ||||||||||
| N | 20,67 | 8505 | 0,04 | B | ||||||||||
| NW | 20,50 | 17236 | 0,03 | C | ||||||||||
| WNW | 20,21 | 3307 | 0,07 | D | ||||||||||
| SW | 20,14 | 5246 | 0,05 | D | ||||||||||
| SSW | 20,07 | 2092 | 0,09 | D | E | |||||||||
| WSW | 19,86 | 2620 | 0,08 | E | F | |||||||||
| E | 19,70 | 19950 | 0,03 | F | ||||||||||
| W | 19,54 | 6373 | 0,05 | G | ||||||||||
| S | 19,45 | 4712 | 0,06 | G | ||||||||||
| SE | 19,36 | 3380 | 0,07 | H | ||||||||||
| ESE | 18,91 | 6278 | 0,05 | I | ||||||||||
| NE | 18,61 | 41399 | 0,02 | J | ||||||||||
| NNE | 18,36 | 564 | 0,16 | J | ||||||||||
| ENE | 18,02 | 55719 | 0,02 | K | ||||||||||
| SSE | 17,94 | 1566 | 0,10 | K |
Medias con una letra común no son significativamente diferentes (p > 0,05)
l ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la temperatura, por causa de las diferentes direcciones o rumbos del viento (tabla 13).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida por 13 categorías de la siguiente forma: La dirección del viento definida por la categoría de Nor Noroeste NNW, muestra en primer lugar, (categoría A) el efecto de una mayor temperatura, con media de 21,35 º C. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor temperatura (º C), con medias de 20,67 para la dirección de viento definida por la categoría Norte N. Se muestran en tercer lugar, (categoría C) el efecto de una menor temperatura (º C), con media de 20,50 para la dirección de viento definida por la categoría Nor oeste NW. Se muestran como cuarta categoría, (categoría D) el efecto de la temperatura, con media desde 20,14 a 20,21 para las direcciones definidas por las categorías Oeste noroeste WNW y Sur Oeste SW (tabla 13).
Los vientos alisios, que circulan entre los trópicos y el ecuador, recorren grandes distancias en sentido noreste - suroeste en el hemisferio norte Pero estos vientos cuando llegan cerca del ecuador ascienden forzosamente y al ascender por la fuerza centrífuga del movimiento de rotación terrestre, producen nubes de desarrollo vertical y lluvias intensas, con lo que su velocidad de traslación disminuye rápidamente. Al enfriarse el aire ascendente y perder la humedad que traían con la condensación y posterior precipitación tenemos un aire frío y seco. Como el aire muy frío es más pesado, tenderá a bajar hacia la superficie formando una especie de plano inclinado que va desde el ecuador hasta los trópicos, siendo su dirección la opuesta a la de los alisios (célula de Hadley). Esta corriente de aire o viento en la zona superior y media de la troposfera va bajando y desviándose hacia la derecha hasta completar el ciclo de los alisios, lo cual coincide con lo demostrado mediante ANOVA, sobre el efecto dirección del viento sobre temperatura, existen diferencias significativas en la temperatura, por causa de los vientos proveniente del Nor Noroeste NNW, norte N. y Nor Oeste NW en relación con los vientos que soplan del Oeste Noroeste WNW, Sur Oeste SW y Sur Sureste SSE.
Relación de Causalidad entre el Dirección del viento y la velocidad del viento
Tabla 14. ANOVA Dirección del Viento (causa), sobre la velocidad del viento Análisis de la varianza
| Variable | N | R2 | R2 AJ | CV |
| Viento10m | 231083 | 0,16 | 0,16 | 52,08 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 1526119,66 | 15 | 101741,31 | 2978,76 | <0,0001 |
| Dirección [rumbos] | 1526119,66 | 15 | 101741,31 | 2978,76 | <0,0001 |
| Error | 7892219,16 | 231067 | 34,16 | ||
| Total | 9418338,82 | 231082 |
Test: LSD Fisher Alfa=0,05 DMS=0,18915
Error: 15,2811 gl: 231062
| Dirección [rumbos] | Medias | n | E.E. | |||||||||||
| ENE | 13,96 | 55719 | 0,02 | A | ||||||||||
| W | 12,66 | 6373 | 0,07 | B | ||||||||||
| NE | 12,21 | 41399 | 0,03 | C | ||||||||||
| NNW | 12,03 | 52131 | 0,03 | D | ||||||||||
| NW | 10,13 | 17240 | 0,04 | E | ||||||||||
| WNW | 9,86 | 3307 | 0,10 | F | ||||||||||
| SW | 9,79 | 5246 | 0,08 | F | ||||||||||
| ESE | 9,38 | 6278 | 0,07 | G | ||||||||||
| SSW | 8,65 | 2092 | 0,13 | H | ||||||||||
| S | 7,49 | 4712 | 0,09 | I | ||||||||||
| WSW | 7,42 | 2620 | 0,11 | I | ||||||||||
| E | 6,47 | 19950 | 0,04 | J | ||||||||||
| SE | 6,44 | 3380 | 0,10 | J | ||||||||||
| N | 6,33 | 8506 | 0,06 | J | ||||||||||
| SSE | 4,00 | 1566 | 0,15 | K | ||||||||||
| NNE | 3,72 | 564 | 0,25 | K |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la velocidad del viento, por causa de las diferentes direcciones o rumbos del viento (tabla 14).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida por 11 categorías de la siguiente forma: La dirección del viento definida por la categoría de Este Noreste ENE, muestra en primer lugar, (categoría A) el efecto de una mayor velocidad del viento, con media de 13,96 m/s. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor velocidad del viento (m/s), con medias de 12,66 para la dirección de viento definida por la categoría oeste W. Se muestran en tercer lugar, (categoría C) el efecto de una menor velocidad del viento (m/s), con media de 12,21 para la dirección de viento definida por la categoría Nor Este NE (tabla 14).
Relación de Causalidad entre el Dirección del Viento y la Potencia Energética Disponible
Tabla 15. ANOVA Dirección del Viento (causa), sobre la RANG [Pdiso10m] RANG_ [Pdisp10m] Análisis de la varianza
| Variable | N | R2 | R2 AJ | CV |
| RANG_[Pdisp10m] | 233915 | 0,18 | 0,18 | 52,21 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 198020439862040,00 | 15 | 13201362657469,40 | 3451,00 | <0,0001 |
| Dirección [rumbos] | 198020439862040,00 | 15 | 13201362657469,40 | 3451,00 | <0,0001 |
| Error | 894751327399257,00 | 233899 | 3825374744,65 | ||
| Total | 1092771767261300,00 | 233914 |
Test: LSD Fisher Alfa=0.05 DMS=2985.93496
Error: 3825374744.6516 gl: 233899
| Dirección [rumbos] Medias | Medias | n | E.E. | |||||||||||
| ENE | 149596,41 | 55719 | 262,02 | A | ||||||||||
| W | 129545,89 | 6373 | 774,76 | B | ||||||||||
| NNW | 128341,44 | 52131 | 270,89 | B | ||||||||||
| NE | 127662,57 | 42105 | 301,42 | C | ||||||||||
| NW | 105838,28 | 17432 | 468,45 | C | ||||||||||
| WNW | 103008,76 | 3307 | 1075,52 | D | ||||||||||
| ESE | 99268,34 | 6278 | 780,60 | E | ||||||||||
| SW | 98940,74 | 5405 | 841,28 | F | ||||||||||
| SSW | 85452,94 | 2092 | 1352,25 | F | ||||||||||
| S | 75276,77 | 4713 | 900,92 | G | ||||||||||
| WSW | 75041,24 | 2620 | 1208,33 | H | ||||||||||
| SE | 66368,76 | 3403 | 1060,24 | H | ||||||||||
| E | 65481,98 | 20818 | 428,66 | I | ||||||||||
| N | 62820,95 | 9389 | 638,30 | J | ||||||||||
| SSE | 37844,60 | 1566 | 1562,94 | K | ||||||||||
| NNE | 36286,82 | 564 | 2604,34 | K |
Medias con una letra común no son significativamente diferentes (p > 0.05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la potencia energética disponible a 10 m de altura, por causa de las diferentes direcciones o rumbos del viento (tabla 15).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: La dirección del viento definida por la categoría de Este noreste ENE, muestra en primer lugar, (categoría A) el efecto de una mayor potencia disponible a 10 m de altura, con media de 2376,23 W/m2. Así mismo, se muestran en segundo lugar, (categoría BC) el efecto de una menor potencia disponible (W/m2), para la dirección de viento definida por la categoría Oeste W. Se muestran en tercer lugar, (categoría BC) el efecto de una menor potencia disponible (W/m2), para la dirección de viento definida por la categoría Nor Noroeste NNW (tabla 15).
Mediante ANOVA se demostró el efecto de la dirección del Viento (causa), sobre la potencia energética disponible, indicando la existencia de mayor potencia energética disponible por causa de las direcciones provenientes del Este Noreste ENE, Oeste W y Norte Noroeste NNW, que las provenientes del sur este SE, Sur S y Sur Sureste SSE; , lo cual coincide con el principio de conservación de la materia que formulara Lavoisier ya que el movimiento del aire en la troposfera, siempre tiene dos componentes: la horizontal, que es la más importante (cientos y hasta miles de km) y la vertical (10 km o más) que siempre compensa, con el ascenso o el descenso del aire, el movimiento horizontal del mismo y los alisios se ven compensados casi perfectamente por los vientos en altura que fueron denominados contralisios.
Relación de Causalidad entre el Velocidad del viento y la potencia energética disponible
Tabla 16. ANOVA Velocidad del viento (causa) sobre la potencia energética10m RANG_[Pdisp10m]
| Variable | N | R2 | R2 AJ | CV |
| RANG_[Pdisp10m] | 236909 | 0,98 | 0,98 | 7,29 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo | 1090354125376310,00 | 12 | 90862843781359,50 | 1217649,50 | <0,0001 |
| Beaufort | 1090354125376310,00 | 12 | 90862843781359,30 | 1217649,50 | <0,0001 |
| Error | 17677537056122,10 | 236896 | 74621509,25 | ||
| Total | 1108031662432440,00 | 236908 |
Test: LSD Fisher Alfa=0,05 DMS=491,31790
Error: 74621509,2535 gl: 236896
| Beaufort | Medias | n | E.E. | |||||||||||
| Temporal huracanado | 236713,50 | 392 | 436,30 | A | ||||||||||
| Temporal muy duro | 236264,50 | 506 | 384,02 | A | ||||||||||
| Temporal duro | 234141,50 | 3740 | 141,25 | B | ||||||||||
| Temporal fuerte | 224946,00 | 14651 | 71,37 | C | ||||||||||
| Temporal | 203197,50 | 28846 | 50,86 | D | ||||||||||
| Viento fuerte | 170662,50 | 36224 | 45,39 | E | ||||||||||
| Brisa fuerte | 134595,50 | 35910 | 45,59 | F | ||||||||||
| Brisa fresca | 101596,50 | 30088 | 49,80 | G | ||||||||||
| Brisa débil | 38347,50 | 26884 | 52,68 | H | ||||||||||
| Brisa muy débil | 18242,50 | 13326 | 74,83 | I | ||||||||||
| Ventolina | 8540,50 | 6078 | 110,80 | J | ||||||||||
| Calma | 2751,00 | 5501 | 116,47 | K |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la potencia energética disponible a 10 m de altura, por causa de las diferentes velocidades de viento (tabla 16).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: La velocidad de viento definida por la categoría temporal huracanado y temporal muy duro, muestra en primer lugar, (categoría A) el efecto de una mayor potencia disponible a 10 m de altura, con media de 53339,10 W/m2 y 16202,88 W/m2 para temporal muy duro. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor potencia disponible (W/m2), con media 10579,81 W/ m2 para la velocidad de viento definida por la categoría temporal duro. Se muestran en tercer lugar, (categoría el efecto de una menor potencia disponible (W/m2), con media 6762,31 W/m2 para la velocidad de viento definida por la categoría Temporal fuerte; Se muestra en cuarto lugar (categoría D), el efecto de una menor potencia disponible (W/m2), con media 4073,78 W/m2 para la velocidad de viento definida por la categoría Temporal (tabla 16).
Relación de Causalidad entre Horario diurno-nocturno sobre la Velocidad del Viento
Tabla 17. ANOVA horario diurno/nocturno sobre la velocidad del viento a 10m Análisis de la varianza
| Variable | N | R² | R² Aj | CV |
| Vel del Viento10m | 236909 | 1,3E-04 | 1,2E-04 | 57,87 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 1269,67 | 1 | 1269,67 | 29,95 | <0,0001 |
| horario | 1269,67 | 1 | 1269,67 | 29,95 | <0,0001 |
| Error | 10042736,03 | 42,39 | 236907 | ||
| Total | 10044005,70 | 236908 |
Test: LSD Fisher Alfa=0,05 DMS=0,05244
Error: 42,3910 gl: 236907
| Horario | Medias | n | E.E. | |
| Día | 11,32 | 118423 | 0,02 | A |
| Noche | 11,18 | 118486 | 0,02 | B |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la velocidad del viento a 10 m, por causa de los diferentes horarios durante el día y la noche (tabla 17).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: El horario definido por el día muestra, (categoría A) el efecto de una mayor velocidad del viento, con media de 11.32 m/s. Así mismo, se muestran en segundo lugar, (categoría B) el efecto de una menor velocidad del viento, con media 11.18 para la velocidad de viento definida por la categoría noche.
Esto indica que hay mayor velocidad del viento a 10 m durante el día que por la noche (tabla 17).
Existe mayor velocidad del viento, durante el día que, por la noche debido al calentamiento solar de la atmosfera durante el día, ya que el aire es diatérmano, este calentamiento es indirecto y se produce cuando entra en contacto con el calor de la superficie de océanos y continentes. Entonces el aire caliente se dilata y disminuye su densidad, por lo que se eleva hasta la parte alta de la troposfera por convección, lo cual coincide con lo demostrado mediante ANOVA del efecto del horario diurno/nocturno sobre la velocidad del viento; encontrándose que el horario definido por el día, presenta el efecto de una mayor velocidad del viento, con media de 11.32 m/s y el efecto de una menor velocidad del viento, con media 11.18 m/s para la velocidad de viento durante la noche.
Relación de Causalidad entre Estación (lluviosa–seca) sobre la Velocidad del Viento
Tabla 18. ANOVA estación sobre la velocidad del viento a 10 m Análisis de la varianza
| Variable | N | R² | R² Aj | CV |
| Vel del Viento10m | 236909 | 0,01 | 0,01 | 57,63 |
Cuadro de Análisis de la Varianza (SC tipo III)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 84220,90 | 1 | 84220,90 | 2003,31 | <0,0001 |
| Estación | 84220,90 | 1 | 84220,90 | 2003,31 | <0,0001 |
| Error | 9959784,80 | 236907 | 42,04 | ||
| Total | 10044005,70 | 236908 |
Test: LSD Fisher Alfa=0,05 DMS=0,05228
Error: 42,0409 gl: 236907
| Estación | Medias | n | E.E. | |
| SECA | 11,88 | 112722 | 0,02 | A |
| LLUVIOSA | 10,68 | 124187 | 0,02 | B |
Medias con una letra común no son significativamente diferentes (p > 0,05)
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística significativa. Por lo tanto, el Análisis de Varianza o Prueba F de Fisher, demostró que existen diferencias significativas en la velocidad del viento a 10 m, por causa de las diferentes estaciones seca y lluviosa (tabla 18).
El Test LSD de Fisher con un Alfa = 0,05, aportó las evidencias estadísticas de una clasificación definida de la siguiente forma: La estación definida como seca, (categoría A) muestra el efecto de una mayor velocidad del viento, con media de 11.88 m/s. Así mismo, se muestran en segundo lugar, (categoría el efecto de una menor velocidad del viento, con media 10.68 (m/s) para la velocidad de viento definida por la categoría lluviosa. Esto indica que hay mayor velocidad del viento durante la estación seca que durante la estación lluviosa (tabla 18).
Debido a la convergencia intertropical explicado por el modelo de circulación atmosférica (Carl-Gustaf Rossby, 1941), en la que se presentan vientos del este y noreste con mayor intensidad durante la estación seca de noviembre a abril que los vientos menos constantes del sur, sureste y suroeste durante la estación lluviosa; lo cual coincide a lo comprobado mediante ANOVA, sobre el efecto de la estación sobre velocidad del viento, indicando para la estación, el efecto de una mayor velocidad del viento, con media de 11.88 m/s, que durante la estación lluviosa con el efecto de una menor velocidad del viento, con media 10.68 (m/s).
Relación de Causalidad Bifactorial
La existencia de métodos estadísticos para comprobar la causalidad entre dos variables (Fisher, 1935) asentó la inferencia estadística lo que coincide con resultados obtenidos mediante ANOVA Bifactorial se demostró el efecto simultaneo de los factores sitio * velocidad del viento sobre potencia energética disponible y sitio * dirección del viento sobre potencia energética disponible.
Entre Sitio y Velocidad del Viento sobre Potencia Energética Disponible
Tabla 19 ANOVA Bifactorial SITIO * Velocidad del Viento, sobre La Potencia Energética Disponible Análisis de la varianza
| Variable | N | R² | R² Aj | CV |
| RANG_[Pdisp10m] | 236909 | 1,00 | 1,00 | 2,61 |
Cuadro de Análisis de la Varianza (SC tipo I)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 1105775093309070,00 | 69 | 16025725989986,50 | 1681985,67 | <0,0001 |
| Sitio | 97722995525130,90 | 1 | 97722995525130,90 | 10256551,11 | <0,0001 |
| CATViento10m | 1008030976080130,00 | 34 | 29647969884709,80 | 3111713,03 | <0,0001 |
| Sitio*CATViento10m | 21121703802,31 | 34 | 621226582,42 | 65,20 | <0,0001 |
| Error | 2256569123367,46 | 236839 | 9527861,22 | ||
| Total | 1108031662432440,00 | 236908 |
El ANOVA realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05, esto indica que se obtuvo una respuesta estadística altamente significativa. Por lo tanto, el Análisis de Varianza, demostró que existe un efecto significativo del sitio (factor principal A) sobre la potencia disponible (tabla 19).
El análisis de varianza realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05 demostró que existe un efecto altamente significativo de la velocidad del viento a 10 m (factor B) sobre la potencia energética disponible a 10 m de altura (tabla 19).
El análisis de varianza realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05 demostró que existe un efecto de la interacción de ambos factores (sitio * Velocidad del viento) simultáneamente sobre potencia energética disponible (tabla 19).
Entre Sitio y dirección del Viento sobre Potencia Energética Disponible
Tabla 20. ANOVA Bifactorial SITIO * RUMBO del Viento, sobre Potencia Disponible 10 m
Análisis de la varianza RANG_[Pdisp10m]
| Variable | N | R² | R² Aj | CV |
| RANG_[Pdisp10m] | 233915 | 0,25 | 0,25 | 50,13 |
Cuadro de Análisis de la Varianza (SC tipo I)
| F.V. | SC | gl | CM | F | p-valor |
| Modelo. | 267959991598392,00 | 31 | 8643870696722,31 | 2451,05 | <0,0001 |
| Sitio | 94573319511383,40 | 1 | 94573319511383,40 | 26817,14 | <0,0001 |
| Rumbos | 120004600769337,00 | 15 | 8000306717955,78 | 2268,56 | <0,0001 |
| Sitio*Rumbos | 53382071317671,60 | 15 | 3558804754511,44 | 1009,13 | <0,0001 |
| Error | 824811775662905,00 | 233883 | 3526599948,11 | ||
| Total | 1092771767261300,00 | 233914 |
El análisis de varianza realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05 demostró que existe un efecto altamente significativo del rumbo (factor B) sobre la potencia energética disponible (tabla 20).
El análisis de varianza realizado aportó las evidencias estadísticas de un valor de p = 0.0001, el cual es menor que el nivel crítico de comparación α = 0.05 demostró que existe un efecto de la interacción de ambos factores (sitio * rumbo) simultáneamente sobre potencia energética disponible (tabla 20).
Análisis Correlacional de Pearson (ANACORR) entre Velocidad del Viento y Potencia disponible
Mediante ANACORR se demuestra asociación fuerte positiva entre las variables velocidad del viento y potencia disponible.
Tabla 21. ANACORR entre las variables Velocidad del Viento y Potencia disponible
Coeficientes de correlación
Correlación de Pearson
| Variable (1) | Variable (2) | n | Pearson | p-valor |
| Vel del Viento10m | [Pdisp10m] | 236909 | 0.74 | <0.0001 |
| Vel del viento20m | [Pdisp20m] | 236909 | 0.74 | <0.0001 |
| Vel del viento30m | Pdisp30m | 236909 | 0.74 | <0.0001 |
| Vel del viento40m | Pdisp40m | 236909 | 0.74 | <0.0001 |
El ANACORR muestra asociación fuerte positiva de la velocidad del viento a diversas alturas y las potencias disponibles.
El análisis de Correlación de Pearson realizado para las variables Vel del Viento10m y Pdisp10m, dio como resultado un coeficiente de correlación “r” igual a 0.74, el cual es un valor próximo a 1, indicando que se tiene una fuerte asociación entre las variables. Este fuerte valor del “r” fue obtenido con un p = 0.0001, el cual resulta ser menor que el nivel crítico de comparación α = 0.05. Por lo tanto, se rechaza la hipótesis nula de Ho: ρ = 0, esto quiere decir que la respuesta estadística obtenida es una correlación significativa, por lo que se demostró que existe correlación entre las variables Vel del Viento10m y Pdisp10m, Vel del Viento20m y Pdisp20m, Vel del Viento30m y Pdisp30m, Vel del Viento40m y Pdisp40m. De ahí que, se confirma la hipótesis de que la velocidad del viento a 10 m. de altura, está asociada con potencia eólica disponible (tabla 21).
Mediante ANACORR se demuestra una fuerte asociación positiva entre las variables velocidad del viento y potencia disponible; lo que coincide con la dependencia de la potencia eólica disponible del cubo de la velocidad del viento.
CONCLUSIONES Y/O RECOMENDACIONES
El municipio de San Nicolás dispone de un importante potencial eólico producto de un valioso recurso existente en la zona como es su VIENTO, medido durante 40 meses, de abril a diciembre 2012, 2013,
2014, diciembre 2017, enero a julio 2018, en una media de velocidad del viento de 11.19 m/s y con dirección del viento prevaleciente, proveniente del Este Noreste ENE (67. 50º) provocado por los vientos alisios. El análisis de 236909 registros de datos mediante correlaciones estadísticas de Pearson permitió comprobar correlaciones significativas de factores ambientales como Altitud y velocidad del viento, temperatura y velocidad del viento, humedad relativa y velocidad del viento, presión y velocidad del viento, dirección y velocidad del viento, temperatura y densidad del aire.
Mediante ANOVA unifactorial se estableció relación significativa de causalidad de las variables: Sitio sobre temperatura, indicando que San José de la Laguna, muestra mayor temperatura con media de 20.39 ºC, que El Sesteo con medias de 19.31 ºC. Sitio sobre velocidad del viento indicando que El Sesteo, muestra el efecto de una mayor velocidad del viento, con media de 12.10 m/s que San José de La Laguna con el efecto de una menor velocidad del viento, con medias de 8.02 m/s. Sitio sobre potencia disponible indicando que El Sesteo, muestra el efecto de una mayor potencia disponible con media de 2088,93 W/m2 que San José de La Laguna con el efecto de una menor potencia disponible, con medias de 901,88 W/m2.
También se realizaron ANOVA que demostraron las causalidades: Dirección del viento sobre temperatura indicando que la dirección del viento Nor Noroeste NNW, muestra el efecto de una mayor temperatura, con media de 21,35 º C. Dirección del viento sobre la potencia disponible indicando que la dirección del viento definida por la categoría de Este Noreste ENE, muestra en primer lugar el efecto de una mayor potencia disponible a 10 m de altura, con media de 2376,23 W/m2. Horario diurno/nocturno sobre la velocidad del viento indicando que, durante el día, se presenta el efecto de una mayor velocidad del viento, con media de 11.32 m/s, que durante la noche con media 11.18 m/s. Estación (seca–lluviosa) sobre velocidad del viento, indicando que hay mayor velocidad del viento durante la estación seca que durante la estación lluviosa.
Mediante ANOVA bifactoriales se estableció relación significativa de causalidad de las variables: Sitio * velocidad del viento sobre potencia energética disponible demostrando que existe un efecto de la interacción de ambos factores (sitio * Velocidad del viento) simultáneamente sobre potencia energética disponible. Sitio * rumbo del Viento sobre potencia energética disponible demostrando que existe un efecto de la interacción de ambos factores (sitio*rumbo) simultáneamente sobre potencia energética disponible. Mediante ANACORR se demuestra una fuerte asociación positiva entre las variables velocidad del viento y potencia disponible. La demostración de estas causalidades permitió determinar el sitio El Sesteo como el apropiado para el emplazamiento de los aerogeneradores y su orientación hacia el Este Noreste ENE.
REFERENCIAS BIBLIOGRÁFICAS
Andressen L, R., & La Rosa, C. (2012). Energía eólica. Evaluación meteorológica de su aprovechamiento en Venezuela. Terra Nueva Etapa [en linea](XXVIII (Enero-Junio)). Recuperado el 9 de febrero de 2017, de http://www.redalyc.org/comocitar.oa?id=72125050004
Canales, F. H., Alvarado, E. L., & Pineda, E. B. (1994). Metodología de la investigación. Manual para el desarrollo de personal de salud. Washington, D.C.: Organizción Panamericana para la Salud.
Diamond, J. (1986). Laboratory experiments, field experiments,and natural experiments. (R. J. Quintanilla, Trad.) New York: Community Ecology. Harper and Row.
ENATREL. (23 de Noviembre de 2016). Octubre Victorioso: 90 % de Nicaragua con energía eléctrica de calidad. Recuperado el 25 de febrero de 2017, de ENATREL. Empresa Nacional de Transmisión Eléctrica: http://www.enatrel.gob.ni
Hernández Escobedo, Q., Espinoza Arenal, F., Saldaña Flores, R., & Rivera Blanco, C. (2012). Evaluación del potencial eólico para la generación de energía eléctrica en el estado de Veracruz, México. DYNA, 79(171), 215-221. Recuperado el 15 de enero de 2017, de https://revistas.unal.edu.co/index.php/dyna/article/view/29599/39118
Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, M. d. (2014). Metodología de la investigación (Sexta edición ed.). México DF: Mc Graw Hill.
Instituto Nacional de Información de Desarrollo INIDE. (2008). San Nicolás en cifras. INIDE, Managua.
Pedroza Henry , & Dicovskiy , L. (2006). Sistema de análisis estadístico con SPSS. Managua: IICA/INTA.
Pedroza, M. E. (1993). Fundamentos de Experimentación Agrícola. Centro de Estudio de Ecodesarrollo para el Trópico (Primera ed.). Managua: Editora de Arte, S. A. (EDITARTE).
Rivera, T. E. (18 de Diciembre de 2009). Blog en Monografias.com. Recuperado el 26 de marzo de 2019, de http://blogs.monografias.com/geologia-peligros-naturales-geotecnologia/2009/12/18/clima-de-nicaragua/
Rodríguez, D. M. (2010). Evaluación del potencial eólico máximo instalable en la isla de Gran Canaria. Instituto Tecnológico de Canarias, Departamento de Energías Renovables. Canarias: Gobierno de Canarias. Obtenido de https://docplayer.es/5821070-Dunia-mentado-rodriguez-departamento-de-energias-renovables-division-de-investigacion-y-desarrollo-tecnologico-instituto-tecnologico-de-canarias.html
© 2019 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
