DOI: https://doi.org/10.5377/farem.v0i30.7883
https://rcientificaesteli.unan.edu.ni

La integral definida como el área bajo una curva en un entorno computacional

The integral defined as the area under a curve in a computational environment

Julia Argentina Granera Rugama1
jgranera@unanfaremesteli.net

Recibido: 18 de enero de 2019, Aceptado: 16 de mayo de 2019

1 Doctora en Matemática Aplicada. Docente del Departamento de Ciencia, Tecnología y Salud. UNAN-Managua/FAREM-Estelí

RESUMEN

El presente trabajo constituye un resumen de la tesis doctoral, “Proceso de enseñanza – aprendizaje de la integral definida como el área bajo una curva en las asignaturas de Cálculo en las carreras de Ingeniería. Estudio realizado en la Facultad Regional Multidisciplinaria, Estelí. (FAREM – Estelí)”. El campo científico en el que está ubicado este estudio es la Didáctica de la Matemática, dentro de las líneas de investigación de la Calidad Educativa. El propósito de la investigación fue desarrollar el campo conceptual del Cálculo y su enseñanza aprendizaje, considerando dos aspectos principales: Un primer aspecto, de ámbito cognitivo mediante el cual se preparó material curricular con el objetivo de introducir previamente al estudio del cálculo de primitivas, el concepto de Integral Definida como área bajo una curva, desde una perspectiva gráfica y numérica. El segundo aspecto, de ámbito afectivo consistió en analizar las actitudes de los estudiantes en torno a confianza, seguridad, motivación, compromiso y uso de la computadora en el trabajo matemático. Los estudiantes fueron seleccionados de los cursantes de la asignatura Cálculo Diferencial e Integral en Ingeniería Ambiental e Ingeniería en Energías Renovables. Se concluye que, la elaboración de un compendio es un instrumento útil en la enseñanza y aprendizaje del Cálculo; y, en relación a las actitudes se tiene que, el uso de la computadora da confianza y seguridad, además de ser motivante y compromete al estudiante en la realización de actividades matemáticas.

Palabras claves: proceso de enseñanza-aprendizaje; Cálculo; actitudes.

ABSTRACT

This paper is a summary of the doctoral thesis, “Teaching-learning process of the definite integral as an area under a curve in the course of calculus for engineering students in the Multidisciplinary Regional Faculty of Estelí. (FAREM – Estelí) . The scientific field within which this study is located in the Didactics of Mathematics, in the research area of educational quality. This research aimed to develop the conceptual field of calculus and its teaching-learning. Two main aspects are considered: first, its cognitive scope through which curricular material was prepared with the objective of introducing a primary study of the calculation of primitives, the concept of definite integral as an area under a curve from a graphical and numerical perspective. The second was an affective aspect consisting of analyzing the attitudes of the students about confidence, security, motivation, commitment, and use of the computer in the mathematical work. The selected students ware taking the differential and Integral calculus course in the discipline of Environmental Engineering and Renewable Energies Engineering. It is concluded that the elaboration of a compendium is a useful tool in the teaching and learning of calculus. Concerning the attitudes, it was found that the use of the computer gives confidence and security. In addition to being motivating, it engages the student in the realization of mathematical activities.

Keywords: teaching-learning process; calculation; attitudes.

INTRODUCCIÓN

La UNAN-Managua, en su Modelo Educativo 2011, plantea que el proceso de enseñanza-aprendizaje debe estar centrado en el estudiante. De ahí que, se pretende que éste asuma un rol activo, participativo y con una alta responsabilidad, con miras a que su formación profesional sea integral con sólidos valores y con un espíritu humanista, además de ser seres pensantes, críticos, creativos e innovadores (UNAN, 2011).  Es en esta visión que se hacen esfuerzos por la implementación de metodologías de aprendizaje activas.

Se considera que las Tecnologías de la Información y Comunicación (TIC) han revolucionado al mundo entero y dan paso a la innovación educativa, que cada vez más requiere estar presentes en los procesos de formación profesional demandados por la sociedad actual. En consecuencia, el uso de los medios tecnológicos demanda una nueva configuración del proceso didáctico y de la metodología, pues los contenidos a desarrollar no deben estar exclusivamente en manos del docente sino que los estudiantes han de ser constructores de su propio aprendizaje.

En diferentes partes del mundo, se ha venido observando que es necesario introducir cambios al interior de las aulas de clase. Esto es algo que viene considerándose seriamente, y que se debe reflexionar en las aulas de Ingeniería una vez que se reconoce la necesidad de brindar aportes para la mejora de los procesos de enseñanza.

En los últimos años se ha visto una preocupación creciente por los métodos de enseñanza– aprendizaje del Cálculo, debido a los elevados niveles de fracaso estudiantil. Varias investigaciones indican que el problema está en la comprensión y manejo de los conceptos de límite, diferenciación e integración. Por un lado, la enseñanza del Cálculo se concentra en habilidades de proceso en lugar de la comprensión conceptual, y por el otro, los conceptos de las matemáticas avanzadas tienen una complejidad intrínseca, que no pueden entenderse sin una sólida comprensión de los conceptos básicos previos (Turégano, 1998).

Según Llorens & Santonja (1997), generalmente en los cursos de Cálculo Integral y la mayoría de textos se consideran dos grandes momentos. En primer lugar, podemos comprobar que la secuencia de contenidos en el apartado de Cálculo integral es siempre la misma: Cálculo de primitivas, Métodos de integración, La integral definida, Aplicaciones de la integración: Cálculo de áreas y volúmenes. En segundo lugar, el nivel de profundidad en cada uno de esos contenidos suele ser diferente, llevándose la mayor cantidad de horas clases los dos primeros, porque el objetivo es que los estudiantes adquieran destrezas en el cálculo de primitivas, trucos matemáticos y recetas para la obtención del resultado.

También, se puede constatar que en muchos textos se omite una revisión del concepto de área; al ser éste un “concepto intuitivo” para interpretar de ese modo las integrales, justificando todo el tedioso cálculo de primitivas. Además, en los últimos años se está generalizando el uso de software, para computadoras y calculadoras científicas que realicen diferentes operaciones y actividades matemáticas como la integración. En estas circunstancias, se considera más importante el significado y estudio de algunos métodos de integración numérica con el uso de las nuevas tecnologías.

Salinas & Alanís (2009), mencionan que la enseñanza tradicional del Cálculo propicia que los docentes centremos la evaluación en la capacidad que logran los estudiantes para aplicar algoritmos y procesos algebraicos en la resolución de ejercicios. Por otra parte, los estudiantes no prestan interés por comprender los conceptos matemáticos, sino más bien que procuran aprender procesos mecánicos de resolución de ejercicios.

Relacionado con lo anterior, en los trabajos diversos autores (Chalmers, 1990; Holton, 1996; Wolpert, 1992; Dunbar, 1999), citados por Solbes (2007) concluyen que existe un desinterés generalizado e incluso rechazo por parte de los estudiantes hacia el aprendizaje de las ciencias y en particular de la matemática. Asimismo afirman, que el mayor nivel de fracaso se debe al impacto emocional que representa el ingreso a las aulas universitarias.

Los mismos autores destacan que los estudiantes no aprenden ciencias y llegan a los estudios superiores con muy mala base. Esta situación, junto con la cantidad de contenidos abstractos y los otros factores ya mencionados, ha provocado que los estudiantes universitarios disminuyan el interés por el aprendizaje consciente de la matemática en general y el cálculo en particular.

Los diagnósticos de investigaciones realizadas muestran que los aprendizajes conceptuales y de aplicación son escasos. Principalmente en matemática, existe poca visualización y contextualización de las propiedades de los conceptos; así como, poca vinculación cognitiva de aspectos gráfico-visuales y analítico–algorítmicos de los mismos.

Desde nuestra experiencia, introducimos el concepto de integral definida en forma expositiva, evitando el verdadero propósito que consiste en obtener aproximaciones cada vez más precisas, predominando el formalismo en el abordaje de los conceptos y la ausencia de asociación con un enfoque geométrico. Esto incide en la comprensión de los mismos y por ende, en la resolución de problemas. Además, en el programa de asignatura se dedica poco tiempo para el desarrollo de contenidos relacionados con los conceptos. En este sentido, se hace necesario rescatar el desarrollo del cálculo haciendo uso de los medios tecnológicos de que se dispone.

En suma, como señala Correa (1999), citado por Aguaded (1989, p. 48), la enseñanza se puede definir como “la acción desarrollada con la intención de llevar a alguien al aprendizaje”. Como bien se señala, la enseñanza trata de un acto consciente e intencional que pretende la consecución de un aprendizaje a través de una serie de acciones.

En virtud de lo anterior, se puede decir que la tecnología, actualmente ha tenido un adelanto exponencial, podría convertirse en un poderoso recurso para el aprendizaje y la enseñanza de las matemáticas, administrada correctamente.

El problema que surge al integrar tecnologías en la enseñanza de la Matemática, en nuestro caso en el cálculo integral, no está en discusión, pero si lo está el cómo llevarlo a la práctica y qué habilidades fomenta o no la utilización de las mismas.

En el mismo orden de ideas, la integración de las TIC en el proceso de la enseñanza - aprendizaje de las matemáticas, es un gran apoyo para el docente que desea que sus estudiantes adquieran un aprendizaje significativo. Al usar las TIC en el aula de clase, podemos encontrar estudiantes muy motivados, ya que ellos están muy familiarizados con el uso de las herramientas tecnológicas, haciendo del aprendizaje un proceso agradable y muy productivo para ellos.

Es de aclarar, que las TIC usadas para apoyar el proceso de enseñanza – aprendizaje de las matemáticas, no son por sí solas, agentes de cambio en la enseñanza de las matemáticas, sino que son una herramienta que el docente tiene a su disposición para apoyarse y generar ambientes diferenciados en el aula.

Cuando se utilizan las TIC, los contenidos de matemática para los estudiantes, son más convincentes. Éstas permiten modelar situaciones problemas, realizar gráficos y elaborar tablas, las cuales facilitan la comprensión de dichos contenidos matemáticos, y al mismo tiempo, promueven una mayor participación y atención en la enseñanza de las matemáticas.

Hitt (2003), asegura que el uso de tecnologías favorece y facilita las diferentes representaciones de los objetos matemáticos, necesarias para construir aprendizaje significativo matemático. Uno de los conceptos que remarca como importante es el de visualización matemática. Explica el autor que para comprender el enunciado de un problema matemático se ponen en juego diferentes representaciones de la cuestión a tratar en él.

También exterioriza que, es importante tener en cuenta la resistencia que muestran los estudiantes en todos los niveles educativos y las dificultades que manifiestan al manipular distintas representaciones para construir conceptos matemáticos,  y a su vez señala que los docentes no tenemos que priorizar alguna de ellas, en detrimento de otras, en el proceso de aprendizaje de un determinado concepto.

Teniendo en cuenta estas investigaciones el autor señala que es importante desarrollar habilidades de visualización en los estudiantes, por ejemplo, haciendo uso de software. Así, si un concepto dado en el lenguaje algebraico no es comprendido por el estudiante, se puede provocar en él una percepción diferente de dicho concepto realizando su representación gráfica y quizás, aquello que resultó ser una interpretación errónea, se pueda corregir.

Siguiendo esta misma idea, Macías (2007) remarca que la matemática se vale de la semiótica y la visualización para representar los conceptos matemáticos, y que ésta es un medio para mejorar la comprensión de dichos entes abstractos. Este proceso de visualización puede realizarse con lápiz y papel, pero el uso de tecnología lo torna más ágil y efectivo.

En relación con lo anterior, podemos afirmar que, la tecnología puede ayudar a los estudiantes a aprender matemática, ya que pueden examinar ejemplos o formas de representar los conceptos, utilizando el poder gráfico de estas herramientas, lo que permite el acceso a modelos visuales poderosos. De esta manera, el aprendizaje se ve favorecido por la retroalimentación brindada por la tecnología, ya que permite modificar gráficos en la pantalla, observar las consecuencias de un valor dependiente de algún parámetro, transformaciones dinámicas, entre otras.

En ese mismo sentido, podemos mencionar que, los programas en la enseñanza de las matemáticas juegan un papel muy importante siempre y cuando se le dé una adecuada y eficiente utilización para la comprensión de los conceptos matemáticos. La idea es utilizar estos programas con la finalidad de visualizar con mayor precisión y comodidad las construcciones matemáticas, comprender con mayor facilidad y motivación algunas fases de la construcción de estructuras matemáticas y demostraciones, implementar estrategias heurísticas en la resolución de problemas y fomentar la independencia y creatividad de los estudiantes.

En definitiva, el aspecto central en cuanto al aprendizaje con la ayuda de la computadora radica en una adecuada interacción entre los programas seleccionados, el papel de los docentes, las acciones de los estudiantes y las actividades concretas de aprendizaje, sin obviar que la presencia activa y formadora de los docentes, es indispensable ya que son ellos en quienes recae con mayor peso la responsabilidad pedagógica y didáctica, pues no puede concebirse una sociedad integralmente "educada" sin su presencia formadora.

Podríamos decir, finalmente, que la computadora se ha convertido en un recurso o medio indispensable para el adecuado desarrollo del proceso de aprendizaje y enseñanza de todas las asignaturas, particularmente de la matemática. Ella, sin embargo, no debería sustituir, por ningún motivo, la presencia y el papel fundamental que jugamos los docentes.

Como  se señala anteriormente, en la actualidad el uso de las TIC se ha convertido en una poderosa herramienta en la enseñanza, que mediante un uso correctamente orientado apoya a la visualización matemática, facilitando la comprensión de conceptos. Es así como, en Internet se pueden encontrar una gran variedad de software educativos, y los software matemáticos no son la excepción.

Uno de los softwares, que se puede descargar en forma gratuita es Geogebra y con el cual proponemos trabajar el concepto de Integral definida, como área bajo la curva. Este programa trae incorporados comandos que calculan y grafican el área bajo una curva utilizando rectángulos y trapecios inscritos y circunscritos, lo que permite a los estudiantes observar y conjeturar respecto a dicho concepto.

Por lo señalado, esta propuesta se fundamenta en que, uno de los recursos didácticos que facilita los procesos de enseñanza aprendizaje para transmitir la naturaleza dinámica de un concepto a partir de la visualización es la computadora. De igual manera, facilita la coordinación de los distintos registros de representación de un concepto, así como la creación de medios personalizados que mejor se adapten a los requerimientos pedagógicos. Además, facilita el factor motivación de manera que los estudiantes reafirmen los conocimientos teórico– prácticos necesarios para el alcance exitoso de los objetivos de la asignatura.

La parte innovadora del presente estudio es precisamente proponer la inclusión de una metodología didáctica que permita mejorar el proceso de enseñanza del cálculo en la universidad, especialmente en Ingeniería. El aporte práctico tanto para el docente como para los estudiantes, es poder optar por esta forma de enseñanza-aprendizaje, ya que este último se realiza en forma computacional, trata de adaptar la teoría a la realidad. A su vez facilita al docente en su tarea mediante actividades sencillas. Asimismo, los estudiantes mejorarán su aprendizaje, estarán motivados y llevarán a la práctica lo aprendido, despertando interés y entusiasmo, al ser partícipes del proceso.

Se considera que esta investigación fue factible, necesaria  y oportuna no solo para la Facultad, sino para la UNAN- Managua, que está inmersa en un proceso de cambio hacia un Nuevo Modelo Educativo con el propósito de transformar la enseñanza tradicional, centrada en el docente, en una entidad activa donde el estudiante debe ser gestor de su propio desarrollo y formación integral. Por otro lado, los docentes serán los facilitadores, diseñadores, comunicadores, coordinadores, asesores, orientadores y evaluadores en el proceso de aprendizaje.

En el aspecto metodológico, beneficia a los docentes interesados en aplicar metodologías activas, con miras a la mejora continua del proceso de aprendizaje. Además, este estudio servirá de base para otras investigaciones que tengan como interés principal profundizar sobre la temática. La novedad científica está dada en la introducción coherente de la computadora como medio auxiliar didáctico para el proceso de enseñanza–aprendizaje de la unidad de Integral Definida como área bajo la curva en un entorno computacional. Al incorporar herramientas computacionales se brinda la posibilidad de ofrecer medios de expresión matemática alternativos, formas innovadoras de manipulación de los objetos matemáticos y estrategias de acercamiento al conocimiento matemático.

Se considera que esta investigación tiene impacto social por ser una de las primeras realizadas a nivel de Doctorado en el  área del Cálculo  Integral, mediante la introducción coherente de la computadora como medio auxiliar didáctico para el proceso de enseñanza – aprendizaje. Además, como toda investigación en el área de Didáctica de la Matemática, tiene como objetivo último el de mejorar el aprendizaje de las matemáticas.

Este trabajo investigativo es de carácter descriptivo, se centró en la determinación del proceso de enseñanza–aprendizaje de la integral definida como el área bajo una curva en las asignaturas de Cálculo en las carreras de Ingeniería de la Facultad Regional Multidisciplinaria de Estelí. Se identificaron aspectos que fundamentan teóricamente la elaboración de un compendio metodológico en el aprendizaje del concepto de integral definida como área bajo la curva en un entorno computacional, sustentado esto en el Modelo Educativo de la Universidad que sugiere la utilización de estrategias metodológicas activas, dirigidas a la evaluación  procesual, vinculación de la teoría con la práctica, construcción de aprendizajes, formación de valores, al saber hacer, saber ser y a la promoción del pensamiento crítico y autónomo.

MATERIALES Y MÉTODOS

El alcance de esta investigación, de acuerdo con sus objetivos y el nivel de profundidad, es de tipo descriptivo, ya que comprende la interpretación y análisis de los hechos, vivencias, circunstancias y experiencias en el proceso de enseñanza-aprendizaje del Cálculo Integral. Según el tiempo de realización es transeccional o transversal descriptiva. De modo que, se realizó una descripción detallada de las actividades, vivencias, emociones, hechos, experiencias y situaciones vividas durante el proceso de enseñanza-aprendizaje de dicha asignatura. Se identifica y analiza la problemática que comporta la interacción docente- estudiantes. La metodología empleada es mixta, predominando lo cualitativo.

Además este estudio se inscribe predominantemente en el paradigma interpretativo y desde la perspectiva inductivo- deductiva y holística; porque pretendía describir, comprender e interpretar los componentes del proceso de enseñanza–aprendizaje implementados en la unidad de Integral Definida, es decir, las estrategias metodológicas utilizadas por los docentes y los estilos de aprendizaje de los estudiantes, que favorecen el logro de aprendizajes significativos.

Población y muestra

La población de este estudio estuvo constituida por docentes y estudiantes que imparten y cursan, respectivamente, la asignatura Cálculo Diferencial e Integral y Cálculo II en las carreras de ingeniería. La misma está conformada por 164 estudiantes y cuatro docentes.

La muestra fue conformada por dos docentes y 133 estudiantes, que inicialmente era igual a la población, pero en el momento de la recolección de la información no estuvieron presentes todos. La técnica de muestreo es no probabilística e intencional, ya que los sujetos de investigación fueron seleccionados a criterios y conveniencia de la investigadora. En relación a las autoridades, se entrevistó al Director del Departamento de Ciencia, Tecnología y Salud y a cuatro coordinadores de carrera.

Las fuentes de información:

Técnicas e instrumentos de recogida de datos

De acuerdo con Hernández et al., (2014), recolectar los datos implica elaborar un plan detallado de procedimientos que conduzcan a reunir datos con un propósito específico. Para ello, se utilizaron métodos o técnicas confiables, válidas y objetivas.

Las fases o etapas desarrolladas:

Para iniciar la investigación se realizó un diagnóstico sobre los componentes del proceso de enseñanza–aprendizaje de las asignaturas Cálculo Diferencial e Integral (Cálculo II) impartido en las carreras de ingeniería.

Para ello:

  1. Se hizo un análisis de los programas de asignaturas en torno a objetivos, contenidos, estrategias metodológicas, medios y formas de evaluación.
  2. Se realizaron entrevistas a dos docentes, cuatro coordinadores de carrera y al Director de Departamento.
  3. Se establecieron conversaciones con docentes con una amplia experiencia en este ámbito profesional.
  4. Se aplicaron encuestas a 133 estudiantes.
  5. Se realizaron cuatro observaciones a clases.

Las entrevistas a docentes y observaciones a clases permitieron identificar, entre otras, su formación profesional, sus actitudes para enseñar, sus opiniones sobre la asignatura que imparte, cuáles estrategias metodológicas implementa, su actitud para el uso de las computadoras y enseñanza–aprendizaje mediante el uso de software matemático.

Las observaciones realizadas fueron de carácter descriptivo de tal forma que permitieron percibir e identificar la efectividad de las estrategias metodológicas y recursos didácticos utilizados, así como la actitud tanto de docentes como estudiantes hacia las Matemáticas y uso de computadoras.

Las encuestas a estudiantes permitieron conocer la actitud hacia las Matemáticas, el uso de las computadoras y el aprendizaje con software matemático, en torno a las cuatro categorías de análisis o dimensiones: confianza y seguridad, motivación, compromiso con el trabajo matemático y el uso del ordenador en las actividades matemáticas.

Para medir las actitudes hacia las matemáticas y hacia el uso de los ordenadores para el aprendizaje de las Matemáticas, se aplicó una escala Likert adaptada de Depool (2004), conformada por 34 ítems que categorizamos de manera similar a la de Galbraith Haines (1998). Este instrumento de medición permitió determinar la dirección de la actitud (positiva o negativa; favorable o desfavorable); así como la intensidad de la actitud (alta o baja).

Se hizo una revisión de los materiales e instrumentos utilizados para organizar el estudio definitivo sobre el concepto de la Integral Definida

En relación con la elaboración del compendio metodológico se consideraron los siguientes tópicos:

Procesamiento y análisis de la información

Se inició haciendo una revisión de la literatura relacionada con las actitudes, las TIC y la problemática sobre comprensión del concepto de la Integral Definida. Para determinar las actitudes de los estudiantes, se utilizó una escala tipo Likert, conformada por 34 ítems, siendo las dimensiones que la definen: confianza y seguridad, motivación, compromiso con el trabajo matemático y uso del ordenador en las actividades matemáticas. Inicialmente, las variables consideradas fueron género, carrera y condición de estudio, pero al momento de aplicar la encuesta se obtuvo que solamente siete de los estudiantes eran repitentes, por lo que en el análisis se obvió esta última.

Para codificar las respuestas se asignaron códigos a cada ítem, teniendo en cuenta si el enunciado se presentaba en forma positiva (+) o negativa (-). El procesamiento de los datos se realizó con SPSS v.22 y Excel. La confiabilidad del instrumento de acuerdo al Alfa de Cronbach fue de 0.8.

El análisis documental se concretó mediante la revisión de bibliografía, Modelo Educativo, programas de asignatura, plan didáctico y planes de clase. Esto con el propósito de analizar, interpretar y triangular la información.
Algunos aspectos que se tuvieron en consideración tanto en el análisis de los documentos como en las observaciones a clases fueron:

La entrevista individual semi-estructurada estuvo dirigida a dos docentes que imparten la asignatura en las carreras que conforman la muestra, a los coordinadores de carrera y Director de departamento, con la finalidad de indagar sobre las estrategias metodológicas utilizadas en el proceso de aprendizaje de la asignatura. La información se registró en libretas de campo y grabadora digital, la que sirvió para efectuar el análisis cualitativo. Para el análisis de datos cualitativos se utilizó el software ATLASti, el cual permitió ordenar y obtener mejores representaciones sobre la información recolectada.

Los datos cuantitativos, obtenidos de la encuesta, se analizaron utilizando el paquete estadístico SPSS y Excel. De tal manera que se establecieron los perfiles estudiantiles.

ANÁLISIS Y DISCUSIÓN DE RESULTADOS

Descripción del proceso enseñanza–aprendizaje

Al realizar el análisis documental,  se visualizó que las estrategias activas demandan un fuerte componente procedimental-actitudinal, capaz de provocar la metacognición del estudiantado. Ello, como condición inevitable para el logro de un aprendizaje significativo.

En las orientaciones metodológicas del programa de Cálculo Diferencial e Integral, en la unidad “La integral y sus aplicaciones”, se sugiere abordar los contenidos conceptuales a través de conferencias y los procedimentales realizando clases prácticas, basadas en guías de trabajo previamente dadas a los estudiantes. Se enfatiza en la resolución de problemas aplicados al perfil de la carrera.

Igualmente, se recomienda facilitar guías de lectura que sirvan de apoyo en la organización de los contenidos. También, se orienta dedicar suficientes clases prácticas, asignaciones de tareas y evaluaciones, para que los estudiantes reafirmen procedimientos, mediante el uso correcto del concepto de integral, formularios, métodos de integración y algoritmos de integración numérica.
En el programa de asignatura de Cálculo II, en la unidad “La integral”, se sugiere iniciar con preguntas exploratorias, relacionas con el concepto de límite, continuidad y derivada de una función, a través de preguntas directas formuladas por el docente para promover la discusión grupal con enfoque participativo. De igual forma, se enfatiza que, para superar las debilidades encontradas  en  esta  etapa exploratoria se debe  entregar a los  estudiantes  una guía de preguntas y ejercicios para consolidar los conceptos básicos.

A la vez sugiere la utilización de estrategias como las conferencias, indicando que el principal propósito es que el estudiante identifique una función dada y que pueda determinar el método apropiado para calcular la integral de dicha función. También, se plantea orientar a los estudiantes en el uso correcto de las tablas de fórmula de la integral (formulario) y calculadora como un instrumento auxiliar para agilizar la realización de ejercicios o problemas. Además, se recomienda que, el estudio de los teoremas sobre la integral definida se haga sin plantear las demostraciones formales de los mismos, sino haciendo un análisis descriptivo e interpretativo.

También se propone utilizar mapas cognitivos, con el fin de alcanzar un aprendizaje significativo. Para ello, se entregará al estudiante una guía de lectura que deberá desarrollar durante sus horas de estudio independiente.

Finalmente, se expresa la utilización de estrategias como “aprendizaje basado en problemas”, indicando que al estudiante se le entregará una guía de ejercicios en la que se orientará la realización de ejercicios y problemas relativos a la aplicación de los métodos de integración para evaluar integrales. Los docentes entrevistados manifiestan que utilizan otras estrategias no sugeridas en el programa como: esquemas didácticos, guías de cuestionarios, investigación, ejercicios de significación, entre otras. Podemos decir que, en alguna medida, existen fortalezas en la aplicación de estrategias metodológicas, lo que favorece la vinculación con el aprendizaje significativo y con el aprender a aprender.

Es meritorio señalar que, se sugiere la conferencia expositiva y como sabemos con esta metodología los docentes de estas asignaturas suelen apoyarse, en general, en la pizarra y algunas veces en diapositivas. De modo que, éstos se enfocan en la mera transmisión de conocimientos y los estudiantes únicamente son receptores de la información. Como bien lo afirma Ruiz (1994), si los métodos no están en correspondencia con las nuevas exigencias que demanda la Educación Superior, la calidad de los aprendizajes estará en riesgo  y tendremos estudiantes poco creativos e innovadores.

Por otra parte, los programas de asignaturas incluyen un apartado sobre recursos didácticos, donde se recomienda utilizar como recursos: el plan didáctico, guías de trabajo, guías de problemas y formulario, apoyándose en el uso de medios tales como: pizarra, marcadores, estuche geométrico, calculadora y computadora, en dependencia de la disponibilidad de laboratorios de computación.

Al respecto del uso de la computadora, uno de los docentes entrevistados manifestó que algunas veces hace uso de software educativo para verificar respuestas, pero se encuentra con el inconveniente que en los laboratorios de computación no hay disponibilidad para su utilización. Es válido señalar que, lo anterior mencionado por los docentes coincide con lo expresado por las autoridades entrevistadas.

En fin, hemos visualizado que las sugerencias metodológicas son concretas y claras; no obstante, hace falta un mayor énfasis en la contextualización de los contenidos y estrategias más activas como el aprendizaje basado en problemas, aplicando el trabajo colaborativo; aprendizaje basado en proyectos, aprendizaje basado en las TIC, entre otras, ya que todas ellas juegan un papel decisivo para que en el proceso de enseñanza-aprendizaje se tome en cuenta al sujeto que aprende.

De acuerdo con lo observado, se revelan potencialidades en cuanto a la comunicación que se logra entre docentes y estudiantes, y de estos entre sí. También se observa que, se crea un clima que favorece el desarrollo del proceso. Sin embargo, se aprecian dificultades relacionadas con otros indicadores, las que se analizan a continuación.

El tratamiento del contenido recae fundamentalmente en el docente, lo que limita la participación  del  estudiante. Cuando  se orientan  actividades,  no  se precisan  objetivos, bibliografía a utilizar ni se precisa la forma de evaluación. La estructura metodológica (introducción, desarrollo y conclusiones) que se sigue no difiere mucho, aunque los objetivos por lograr sean diferentes.

En suma, es preciso que se produzca un cambio profundo en nuestro quehacer educativo. Perera-Cumerma & Veciana-Pita (2013), plantean que es necesario que pasemos de la aplicación de un modelo unidireccional, en el que el saber se encuentra en los libros o en el docente, a ser multidireccional. Es decir que, hay que ser más abiertos y flexibles, facilitando un ambiente donde reine la curiosidad, la creatividad y la innovación.

Referente al sistema de evaluación, los programas reflejan los parámetros para que el estudiante tenga derecho a presentarse a las evaluaciones sistemáticas y al examen, coincidiendo con lo establecido en el Reglamento de Régimen Académico. Igualmente, se explicita que la evaluación debe ser continua considerando el desempeño de cada una de las actividades de aprendizaje, haciendo especial énfasis en obtener evidencias de aprendizaje como: solución de ejercicios, actividades de investigación, análisis  y discusión grupal, resolución de problemas y examen escrito para comprobar el manejo de aspectos teóricos y prácticos.

Ahora bien, en los planes didácticos de la asignatura la forma de evaluación consignada hace referencia a la modalidad de acuerdo con la función (diagnóstica, formativa y sumativa), y de acuerdo con quien la realiza (autoevaluación, coevaluación y heteroevaluación). A su vez, las estrategias de evaluación reflejadas en el mismo son preguntas introductorias de la asignatura, ejercicios individuales, prueba individual y clases prácticas.

Conforme lo expresado anteriormente, visualizamos que las estrategias de evaluación, como ocurre con las sugerencias metodológicas, son concretas y claras. Así que, se implementa la evaluación de proceso, por lo que es de esperar que estas estrategias formadoras y cualitativas produzcan aprendizaje profundo y de alto rendimiento. No obstante, contradice lo expresado por Hernández (1996), quien afirma que, en el contexto universitario se ha comprobado que la forma en que el profesorado plantea la evaluación de su alumnado afecta a los enfoques de aprendizaje (superficial o profundo) y a la calidad de dichos aprendizajes.

Resumiendo las ideas expresadas se infiere que es preciso utilizar estrategias en que el estudiantado:

Opinión de los docentes sobre el uso de software matemático

Las entrevistas realizadas a docentes, así como a las autoridades universitarias permitieron identificar cuál es la percepción que tienen acerca de la importancia del uso de medios tecnológicos en el desarrollo de las clases. De los dos docentes entrevistados, sólo uno de ellos manifiesta realizar, algunas veces, el proceso de enseñanza-aprendizaje aplicando software matemático. Sin embargo, ambos expresan hacer uso de las redes sociales e Internet en la facilitación de sus clases.

Referente a la preparación informática de los docentes entrevistados, éstos manifestaron que poseen conocimientos en cuanto al dominio de contenidos básicos necesarios para manipular la computadora, aunque haya debilidades en el dominio de asistentes y software matemático. También manifestaron, al igual que las autoridades, que el uso de software educativo favorece la clase. Ello, porque facilita la ejercitación de contenidos y la relación inter- materias, desarrolla habilidades informáticas, motiva a los estudiantes y ayudan al desarrollo de contenidos.

No obstante, plantean que como su perfil no es de informática no hacen uso de medios informáticos. Además, el acceso a los laboratorios es limitado, no se ha capacitado en el uso de estos medios y falta tiempo para usarlo en la clase y cumplir en tiempo las exigencias de los programas. Por su parte, las autoridades destacaron que falta software por instalar y aunque se menciona el uso de la computadora en los programas de estudios, no aparece declarado su uso como una prioridad.

Todo lo expresado anteriormente por los entrevistados fue secundado en conversaciones con docentes de vasta experiencia. Asimismo, se ha constatado desde nuestro contexto que existe un limitado acceso a los laboratorios, lo que responde más a un problema organizativo que a una situación de real disponibilidad.

Como lo señala González (1998), algunos docentes estamos incursionando en jugar un rol más activo, basado en una docencia de calidad,  actuando como facilitador del grupo clase. Es decir, como orientadores, estrategas, expertos no solo en lo científico sino también, en lo metodológico.

Ahora bien, las autoridades valoraron la preparación en informática de los docentes que facilitan las asignaturas, con miras a la utilización del software matemático para el ejercicio de su labor educativa. También expresaron que, las principales necesidades de los docentes de Cálculo para lograr un uso efectivo de los recursos informáticos en el proceso de aprendizaje son: tiempo, capacitación, adquisición de equipos, entre otras.

Finalmente recomiendan a los docentes negociar con los estudiantes para que trabajen con sus portátiles, preparación consensuada de las prácticas de y en el laboratorio, la vinculación a redes de matemáticos para el intercambio de experiencias, entre otras. Esto,  para la conducción del proceso enseñanza-aprendizaje, utilizando un entorno computacional.

Sobre la base de las consideraciones anteriores, de las entrevistas y encuestas aplicadas a los docentes  y directivos con el propósito de diagnosticar la situación sobre el uso de la computadora en el proceso de enseñanza-aprendizaje de la Matemática se resume:

  1. En las actividades docentes controladas se evidencia que:
    • El uso de la computadora en la clase no es sistemático.
    • La orientación de la actividad no se hace con toda la precisión requerida lo que propicia que no se exploten las posibilidades del software educativo.
  2. La preparación informática de los profesores presenta:
    • Potencialidades en cuanto al dominio de los contenidos básicos necesarios para manipular la computadora
    • Debilidades en cuanto al dominio de los asistentes matemáticos y softwares educativos.
  3. Las principales causas por las que los profesores no utilizan la informática están dadas por debilidades en:
    • La orientación metodológica sobre el uso de la computadora como recurso didáctico en el proceso de enseñanza-aprendizaje en general y de la Matemática en particular.
    • La orientación explícita del empleo de los softwares educativos y asistentes matemáticos.
    • La preparación de los profesores para utilizar la computadora en la resolución de los problemas.
  4. Las principales necesidades del departamento y de los profesores con respecto al proceso de enseñanza-aprendizaje de la Matemática asistida por computadoras están encaminadas hacia:
    • La capacitación de los profesores en el uso del software educativo, asistentes matemáticos y sistemas de aplicación, con el objetivo de demostrar las posibilidades que ofrecen los mismos para el proceso de enseñanza-aprendizaje de la Matemática y la resolución de problemas.
    • La preparación metodológica de los profesores encaminada a insertar de una forma coherente y sistémica la computadora en sus clases.

Y bien, se puede decir que, se evidencia, en alguna medida, fortalezas en la preparación de los docentes para la incorporación de los softwares al proceso de enseñanza-aprendizaje de las Matemáticas, en general y del Cálculo en particular como son:

Lo antes expuesto, permite aseverar que, en la medida que el docente reconozca la utilidad que tiene el uso de la computadora y aumente sus habilidades informáticas, contribuirá a la mejora continua del proceso de enseñanza-aprendizaje de la Integral Definida. De modo que, coincidimos con Hitt (2003) en que el uso de tecnologías favorece y facilita las diferentes representaciones de los objetos matemáticos; que son necesarias para construir un conocimiento matemático.

Asimismo, se afirma que, si el docente asume una actitud positiva hacia la herramienta computacional, valorando las virtudes y potencialidades de dicha herramienta, además generando estrategias que lleven a su inclusión en la práctica, tendremos estudiantes creativos e innovadores. Estos podrán dar respuesta y/o solución a las situaciones de aprendizaje en las que se vean involucrados.

Actitud de los estudiantes hacia las Matemáticas y hacia el uso de la computadora

El valor actitudinal de los estudiantes de manera global es positivo, pero podemos considerarlo bajo. La dispersión de los valores actitudinales no son similares en cada grupo de clase; además entre el grupo masculino se observa mayor dispersión en las respuestas que el grupo femenino; esto evidencia heterogeneidad en los valores actitudinales tanto en las mujeres como en los hombres. Al comparar los promedios de los valores actitudinales y las dispersiones en cuanto a género, se observa que existe gran homogeneidad, a excepción del grupo de estudiantes de la carrera de ingeniería industrial.

Similares resultados se obtuvieron para el valor actitudinal de los estudiantes de manera global en las dimensiones (confianza y seguridad, motivación, compromiso con el trabajo matemático). En cuanto al uso de la computadora en actividades matemáticas la actitud tiende a ser negativa, tal vez por el desconocimiento que tienen los estudiantes de los potenciales de este recurso. Tanto los valores actitudinales como la dispersión son similares en cada grupo; esto evidencia gran homogeneidad en los grupos tanto por género como por carrera.

Estos resultados hacen pensar que, contrariamente de lo que se podría pensar sobre la actitud de los estudiantes de las carreras de ingeniería, existe una baja actitud hacia las Matemáticas y el uso de las computadoras.

Dimensión afectiva. Confianza y seguridad en el trabajo matemático

Analizando los promedios en esta dimensión se nota que en la mayoría de los ítems la valoración en torno a la confianza y seguridad hacia el trabajo matemático es alta (5 de 8 ítems). En orden decreciente se observa que los estudiantes le asignan mayor valoración a: Obtener buenas calificaciones en Matemáticas, es importante para ellos; las Matemáticas requieren practicar continuamente; justificar cada paso en Matemáticas es importante y; las Matemáticas ayudan a las personas a pensar lógicamente.

Consideran con una valoración menor que: la imaginación y la intuición son útiles en Matemáticas; las Matemáticas les dan seguridad y al mismo tiempo los estimula y; cuando están en clases de Matemáticas se quedan como “en la luna” y no entienden. La valoración más baja se la asignan a que: los exámenes de matemáticas les producen miedo. También se destaca que los estudiantes de las carreras de Ingeniería Industrial y Agroindustrial le asignan mayor valoración en cada ítem que los otros estudiantes; esta diferencia no es tan significativa en cuanto a género.

De lo anterior se puede concluir que la seguridad y confianza en el trabajo matemático influye significativamente en la actitud de los estudiantes hacia las Matemáticas; que el obtener buenas calificaciones, practicar continuamente y justificar cada paso influye positivamente en la actitud; la imaginación y la intuición en Matemáticas y el hecho de sentirse estimulados por Matemáticas afectan en menor grado a la actitud. Es de hacer notar que los exámenes de Matemáticas al producirles miedo puede disminuir la confianza y seguridad en el trabajo matemático, generando en el estudiante una actitud que se aproxima a lo negativo. Finalmente el género no afecta significativamente la actitud de los estudiantes hacia las Matemáticas.

En el gráfico N° 1, se aprecia el perfil de los estudiantes en esta dimensión:


Gráfico 1. Dimensión afectiva. Confianza y seguridad en el trabajo matemático.
Fuente: Elaboración propia.

Dimensión afectiva. Motivación hacia el trabajo matemático

Analizando los promedios a las respuestas se nota que la valoración es baja en los ítems que definen esta dimensión. En orden decreciente se observa que los estudiantes le asignan mayor valoración a que: prefieren no entrar a clases de Matemáticas y, les agrada resolver problemas matemáticos, así como a que si en la universidad se organiza un club de matemáticas le gustaría participar. La valoración es menor en cuanto a que: las clases de Matemáticas les resultan largas y tediosas. Los valores que reflejan una tendencia hacia una baja motivación se relacionan con: no ser voluntarios para pasar a la pizarra, sentir la necesidad de conversar sobre Matemáticas y que en clases de Matemáticas no presta atención.

También se destaca que generalmente son los estudiantes de las carreras de Ing. Ambiental e Ing. en Energías Renovables los que asignan mayor valoración en cada ítem; esta diferencia, al igual que la dimensión anterior, no es tan significativa en cuanto a género. En conclusión, a pesar de los bajos valores observados, la motivación hacia el trabajo matemático determina una actitud positiva, aunque baja. Detallando las respuestas se encontró que, aunque prefieren entrar a clases de Matemáticas, les gustaría participar en un club y resolver problemas, no les motiva pasar a la pizarra y conversar acerca de esta disciplina. Esto lleva a pensar que posiblemente las clases de Matemáticas no motivan al estudiante a participar en ellas; pero, integrándose a un club o usando la tecnología se sentirían motivados y como consecuencia favorecería una actitud positiva en ellos. Finalmente, el género no afecta significativamente la actitud de los estudiantes hacia las Matemáticas.

El gráfico N° 2, muestra el perfil de los estudiantes en esta dimensión:


Gráfico 2. Dimensión afectiva. Motivación hacia el trabajo matemático.
Fuente: Elaboración propia

Dimensión Cognitiva. Compromiso con el trabajo matemático

Analizando los promedios de esta dimensión se nota que la valoración en torno al compromiso de los estudiantes con el trabajo matemático es alta (9 de 12 ítems). De modo que, esta dimensión determina una actitud positiva hacia las Matemáticas. Sin embargo, contradictoriamente se encontró que, aunque consideran que el conocimiento de la teoría es indispensable para resolver los problemas, el vocabulario propio de esta disciplina hace más difícil su aprendizaje. Además, consideran que conocer cómo resolver un problema es tan importante como hallar su solución, pero a la hora de resolverlos se enredan. Quizás cambiando la estrategia de enfrentar al estudiante con el conocimiento, se podría aumentar el compromiso que involucra la dedicación disciplinada del estudio de las Matemáticas.

De igual manera, consideran que las Matemáticas tienen usos prácticos en la vida diaria, pero señalan que éstas tienen la culpa de que muchos hayan dejado de estudiar. Esto refleja que, se considera a la Matemática útil, pero existen motivos (probablemente la forma habitual de impartirla) para que los estudiantes abandonen sus estudios. Es meritorio analizar que, si al utilizar mecanismos que involucren nuevas tecnologías, como las computadoras, de gran uso en actualidad, podrían los estudiantes comprometerse con el trabajo matemático. Finalmente, se observó que en el género no existen diferencias significativas en la actitud de los estudiantes hacia las Matemáticas. Seguidamente se presenta el perfil de los estudiantes en esta dimensión en el gráfico N° 3.


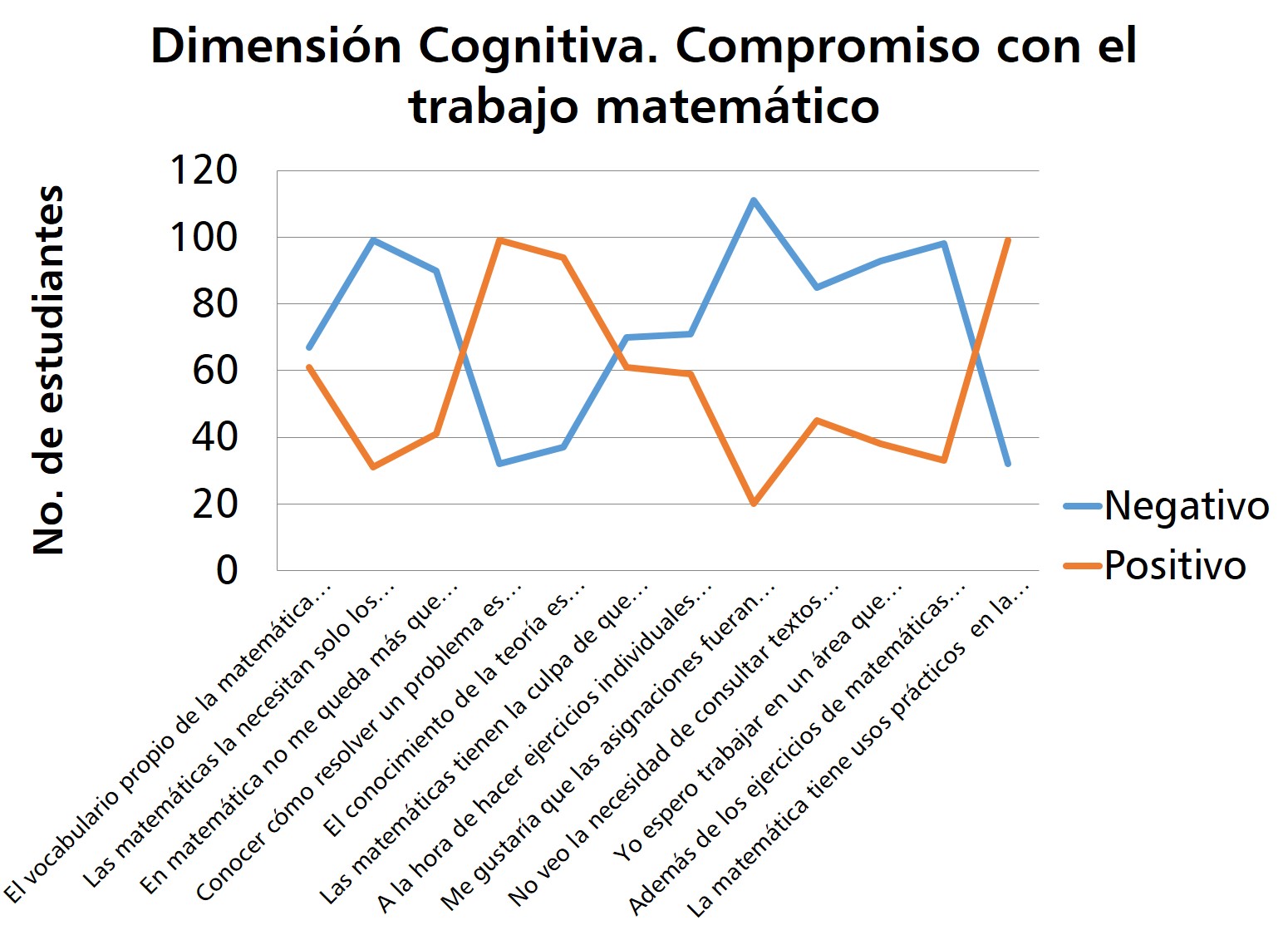
Gráfico 3. Dimensión afectiva. Compromiso con el trabajo matemático.
 Fuente: Elaboración propia.

Dimensión conductual. Uso de ordenadores en actividades Matemáticas

Analizando los promedios de las respuestas en esta dimensión se observa que la valoración hacia el uso de ordenadores en actividades matemáticas es alta solamente para dos de los seis ítems. En orden decreciente se observa que los estudiantes le asignan mayor valoración a que: manejar una computadora no les produce miedo y, que los profesores que dan su clase sin una computadora son obsoletos. Los valores más bajos se tienen en cuanto a que: para trazar una gráfica o para realizar cálculos matemáticos no es necesario usar una computadora.

Así, detallando las respuestas, podemos observar que aunque manejar una computadora no les produce miedo y que están de acuerdo con su uso en clase de Matemáticas, no la consideran una herramienta útil para graficar y realizar cálculos matemáticos.

A continuación se puede ver el perfil de los estudiantes en esta dimensión en el gráfico N° 4:


Gráfico 4 Dimensión conductual. Uso de ordenadores en actividades matemáticas.
Fuente: Elaboración propia

Generalizando, se infiere que:

Atendiendo a los resultados obtenidos en este estudio se propone estructurar nuevamente la experiencia de tal manera que se tomen dos grupos (control y experimental), con los cuales se trabaje, uno con un método tradicional y el otro utilizando computadoras, aplicando el compendio elaborado en este estudio. Al finalizar el desarrollo de los contenidos se les aplicaría una prueba de actitud.

Deficiencia metodológica que presentan los libros de textos recomendados en la asignatura de Cálculo

De manera general se señala que, el tratamiento que se da para la presentación del concepto de integral definida es aceptable. Sin embargo, a pesar que en la mayoría de los libros de texto se enfoca el “nuevo” concepto de área utilizando la integral definida, partiendo del “viejo” concepto de área conocido por los estudiantes, debiera haberse resaltado que área e integral definida son conceptos distintos.

Así también, en los libros analizados no se pudo evidenciar la utilización de las nuevas tecnologías en el cálculo integral, por tanto, se ignoran las calculadoras y los programas de cálculo simbólico; sin embargo, se entiende que son herramientas imprescindibles para la enseñanza y el aprendizaje de la integral. Además, se piensa que hoy en día una razón por la cual es importante el estudio de la integración numérica es por la facilidad de realizar los cálculos con medios informáticos.

Adicionalmente no se proponen elementos extensivos (ejemplos, problemas, actividades) cuyo objetivo sea la conversión entre los diversos registros de representación semiótica. Por ejemplo: la representación gráfica: usando figuras geométricas; la representación algebraica: aplicando fórmulas de áreas de figuras planas; y la representación analítica: planteando particiones del intervalo, sumas de Riemman y el límite de las sumas.

También, es conveniente incluir una pequeña introducción histórica en la cual tendrían que estar, al menos, Arquímedes, Newton, Leibniz y Riemann. ¡No podemos ignorar el pasado y silenciar los avances tecnológicos!

Como un aporte didáctico a los docentes y estudiantes que imparten o cursan la asignatura Cálculo Diferencial e Integral y Cálculo II y resultado de este estudio se elaboró un compendio metodológico, con el propósito de contribuir a generar procesos de aprendizajes significativos. También,  que se facilite el trabajo tanto en el aula como fuera de ésta y que el acto educativo sea más dinámico y enriquecedor.

Es importante señalar que, en la elaboración de este documento se contempló un resumen histórico sobre los aportes de los principales representantes que contribuyeron al desarrollo del Cálculo. Asimismo, se plantean situaciones que retoman conceptos y procedimientos estudiados por los estudiantes en la educación secundaria y en la asignatura Matemática General.

Lo anterior, se plantea de tal manera que invitan al análisis y  reflexión, a la argumentación y experimentación, a la resolución de problemas, a la creatividad e innovación y al disfrute que provoca el aprender haciendo. Todo ello, dirigido a la búsqueda constante de conocimientos y aprendizajes significativos.

CONCLUSIONES

Los resultados de la revisión documental y su correspondiente análisis de contenido permiten fundamentar que:

El Modelo Educativo de la UNAN Managua sugiere la utilización de estrategias metodológicas activas. Éstas están dirigidas a la evaluación procesual, vinculación de la teoría con la práctica, construcción de aprendizajes, formación de valores, al saber hacer, saber ser y a la promoción del pensamiento crítico y autónomo.

En los programas de asignatura las sugerencias metodológicas y estrategias de evaluación son concretas y claras; no obstante, hace falta un mayor énfasis en el desarrollo de aptitudes, habilidades y destrezas. En los planes didácticos de la asignatura la forma de evaluación consignada hace referencia a la modalidad de acuerdo con la función, y de acuerdo con quien la realiza.

Sobre la preparación informática de los docentes se constata que existen potencialidades en cuanto al dominio de contenidos básicos necesarios para manipular la computadora, aunque haya debilidades en cuanto al dominio de asistentes matemáticos y softwares matemáticos.

Además, se evidencia que, en alguna medida, existen fortalezas para la preparación de los docentes en la incorporación de los softwares al proceso de enseñanza-aprendizaje de las Matemáticas, en general y del Cálculo en particular como son: (1) Dominio de las habilidades en informáticas elementales. (2) Dominio de los contenidos de la matemática. (3) Deseos de aprender. (4) Motivación para utilizarlo.

Existe una actitud global positiva hacia las Matemáticas y el uso de las computadoras, aunque no demasiado alta. Se considera que, los estudiantes tienen una actitud positiva hacia las dimensiones confianza y seguridad, motivación y el compromiso con el trabajo matemático, no así hacia el uso del ordenador en actividades matemáticas.

En relación al análisis de libros de textos, el tratamiento que se da para la presentación del concepto de integral definida es aceptable, pero no se considera la utilización de las nuevas tecnologías en el Cálculo Integral. Sin embargo, se considera que son herramientas imprescindibles para la enseñanza y el aprendizaje de la integral.

Referente al compendio metodológico, este contempla un breve desarrollo histórico de los orígenes del Cálculo, se aproxima al concepto de la integral definida, abordando la temática con problemas de exploración relacionados con el cálculo de área de regiones planas, en distintos contextos, para formalizarlo utilizando el software matemático Geogebra. Este compendio será de utilidad a los docentes y estudiantes para la promoción de aprendizajes significativo en la unidad de Integral Definida, pero, no se puede obviar que para el alcance de los objetivos propuestos, debe primar el interés y la motivación.

BIBLIOGRAFÍA

Aguaded G., J. I. (1989). Aprender y enseñar con las tecnologías de la comunicación.
España: Universidad de Huelva.

Depool R., R. A. (2005). La enseñanza y aprendizaje del Cálculo Integral en un entorno computacional. Actitudes de los estudiantes hacia el uso de un Programa de Cálculo Simbolico (PSC). Universidad de La Laguna.

Duval, R. (1998). Registros de representación semiótica y funcionamiento cognitivo del pensamiento. In Investigaciones en Matemática Educativa II (pp. 173–201). México: Cinvestav.

Duval, R. (2004). Semiosis y Pensamiento humano. Registros semióticos y Aprendizajes intelectuales. (U. del Valle, Ed.). Cali: Grupo de Educación Matemática.

Gil, N., Guerrero, E., & Blanco, L. (2006). El dominio afectivo en el aprendizaje de las Matemáticas. Electronic Journal of Research in Educational Psychology, 4(1), 47–72.

González Cabanach, R., Fernández Suárez, A. P., Cuevas González, L. M., & Valle, A. (Valle A. (1998a). Las estrategias de aprendizaje. Características básicas y su relevancia en el contexto escolar. Revista de Psicodidáctica, (6), 53–68. Retrieved From http://dialnet.unirioja.es/servlet/extart?codigo=2002207%5Cnhttp://dialnet.unirioja.es/servlet/articulo?codigo=2002207&orden=1&info=link

González - Martín, A. (2005). La generalización de la integral definida desde las perspectivas numérica, gráfica y simbólica utilizando entornos informáticos. Universidad de La Laguna.

Hernández, F. (1996). La evaluación de los alumnos en el contexto de la evaluación de la calidad de las universidades. Revista de Investigación Educativa, 14(2), 25–50.

Hernández, R., Fernández, C., & Baptista, C. (2014). Metodología de la investigación. Journal of Chemical Information and Modeling (6ta. Edición). McGRAW - HILL.

Hitt, F. (2003). Una Reflexión Sobre la Construcción de Conceptos Matemáticos en  Ambientes con Tecnología. Boletín de La Asociación Matemática Venezolana, X(2),213–223.

Llorens, J. L., & Santonja, F. J. (1997). Una interpretación de las dificultades en el aprendizaje del concepto de integral. Divulgaciones Matemáticas, 5(1–2), 61–76.

Macias Ferrer, D. (2007). Las nuevas tecnologías y el aprendizaje de las matemáticas. Revista Iberoamericana de Educación, 42(4), 1–17. Retrieved from http://www.rieoei.org/deloslectores/1517Macias.pdf

Perera-Cumerma, L. F., & Veciana-Pita, M. (2013). Las TIC como instrumento de  mediación pedagógica y las competencias profesionales de los profesores. VARONA, Revista Científico - Metodológica, (56), 15–22. Retrieved from http://www.redalyc.org/pdf/3606/360633908004.pdf

Ruiz, L. M. (1994). Los métodos de Enseñanza en la Educación Superior. Revista Cubana de Educación Superior, 14(2), 121–124.

Salinas, P., & Alanís, J. A. (2009). Hacia un nuevo paradigma en la enseñanza del Cálculo dentro de una institución educativa. Revista Latinoamericana de Investigación En Matemática Educativa, 12, 355–382. Retrieved from
http://redalyc.uaemex.mx/src/inicio/ArtPdfRed.jsp?iCve=33511859004

Solbes, J. (2007). El desinterés del alumnado hacia el aprendizaje de la ciencia: implicaciones en su enseñanza. Didáctica de Las Ciencias Experimentales Y Sociales, 117(21), 91–117. https://doi.org/10.7203/dces..2428

Turégano, P. (1998). Del área a la integral. Un estudio en el contexto educativo. Enseñanza de Las Ciencias Revista de Investigación y Experiencias Didácticas, 16(2), 233–249.

UNAN-Managua. (2011). Modelo  Educativo, Normativa  y  Metodología  para la Planificación Curricular. Managua: Editorial Universitaria.

© 2019 - Revista Científica de FAREM-Estelí.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.