Aplicación informática para el problema de corte de un tablero

Computer application for the cutting problem of a board

RESUMEN

En el presente artículo se muestra la aplicación de una herramienta informática basada en algoritmos heurísticos eficientes para problemas de corte de tableros empleando el algoritmo Greedy propuesto por Martello y Toth en 1990 (Algoritmo constructivo). (Cánovas , Huertas, & Sempere, 2011) En este particular el algoritmo Greedy se utiliza para encontrar una primera solución (como punto de partida para otra heurística). Para el desarrollo de esta aplicación se utilizó Visual Studio 2010.

Palabras clave: corte de un tablero, Algoritmo Greedy Aplicación informática.

ABSTRACT

This article shows the application of a computer tool based in heuristic algorithms which are efficient for cutting problems of boards using the Greedy algorithm proposed by Martello y Toth in 1990 (Constructive algorithm). (Canovas, Huertas & Sempere, 2011) In this particular case the Greedy algorithm is used to find a first solution (as a starting point for another heuristic) For the development of this application it was used Visual Studio 2010..
Keywords: cutting of a board, Greedy algorithm, computer application.

INTRODUCCIÓN

El método que produce algoritmos ávidos, es un método muy sencillo. Este puede ser aplicado a numerosos problemas, especialmente los de optimización.

El método consiste en: dado un problema con entradas, obtener un subconjunto de éstas que satisfaga una determinada restricción definida para el problema. Cada uno de los subconjuntos que cumplan las restricciones son soluciones prometedoras. Es así que, una solución prometedora que maximice o minimice una función objetivo se denomina solución óptima.

Como ayuda para identificar si un problema es susceptible de ser resuelto por un algoritmo ávido, se definen una serie de elementos que deben están presentes en el problema:

• Un conjunto de candidatos, que corresponden a las entradas del problema.Una función de selección que en cada momento determine el candidato idóneo para formar la solución entre los que aún no han sido seleccionados ni rechazados.
  
• Una función que comprueba si un cierto subconjunto de candidatos es prometedor. Se entiende por prometedor, que sea posible seguir añadiendo candidatos y encontrar una solución.
  
• Una función objetivo que determine el valor de la solución hallada. Es la función que se desea maximizar o minimizar.
  Una función que compruebe si un subconjunto de estas entradas es solución al problema, sea óptima o no.

Con estos elementos, se puede resumir el funcionamiento de los algoritmos ávidos en los siguientes puntos:

1. Para resolver el problema, un algoritmo ávido tratará de encontrar un subconjunto de candidatos, tales que, cumpliendo las restricciones del mismo, constituya la solución óptima.
   
2. Para ello, trabajará por etapas, tomando en cada una de ellas la decisión que le parece mejor, sin considerar las condiciones futuras, y por lo tanto, escogerá entre todos los candidatos, el que produce un óptimo local para esa etapa, suponiendo que será a su vez óptimo global para el problema.
   
3. Antes de añadir un candidato a la solución que está construyendo, comprobará si es prometedora al añadirlo. En caso afirmativo, lo incluirá en ella, y en caso contrario descartará este candidato para siempre y no volverá a considerarlo.
   
4. Cada vez, que se incluye un candidato comprobará si el conjunto obtenido es la solución.
   Se puede resumir, que los algoritmos ávidos constituyen la solución en etapas sucesivas, tratando siempre de tomar la decisión óptima para cada etapa. (Cánovas & Sempere, 2011).
   

DESARROLLO

Para el desarrollo de esta aplicación informática se utilizó la herramienta informática visual Studio 2010.

En el contexto de la Investigación Operativa y bajo el término problemas de Corte y Empaquetado, Cutting and Packing Problems, se engloba un conjunto de problemas de optimización combinatoria para una considerable variedad de aplicaciones industriales: metal, papel, madera, vidrio, textil o piel y calzado, entre otros.

El problema de corte en dos dimensiones consiste en determinar un conjunto de patrones variables, de tal forma que satisfagan los requerimientos de piezas de material solicitados, utilizando el menor número de láminas disponibles. Los cortes en dos dimensiones se clasifican por el tipo de herramienta a utilizar como el corte por guillotina y corte no guillotina, considerados cortes rectangulares aplicados en el sector de papel, vidrio, metal, madera. (Pearl, 1984).

Un ejemplo de aplicación de este tipo de problemas es el estudio de la problemática concreta en el corte de vigas estructurales, en una empresa de transformados metalúrgicos.

El principal objetivo de este problema es reducir la cantidad de desperdicio de material que se origina al momento de realizar determinado corte.

En este sentido, el trabajo permite construir un algoritmo constructivo, para lo cual se propone la utilización de un algoritmo metaheurístico GRASP (Greedy), el cual se utiliza para dar solución al problema de corte en dos dimensiones. En los últimos años el desarrollo de procedimientos que utilizan heurísticas para resolver problemas de este tipo, han sido enormes. ( Ruiz Rivera & Ruiz Lizama, Algoritmo GRASP para cortes de guillotina, 2006).

Un método heurístico frente a uno exacto suministra una solución al problema, la que se considera buena aunque no necesariamente sea la óptima.

• Algunos de los motivos que pueden justificar esta incorporación de las técnicas heurísticas a la resolución de problemas de optimización pueden ser:
• Su flexibilidad al abordar aspectos de complicada modelización.
  Su bajo costo computacional para implementarlas.
  
• La posibilidad de dar soluciones factibles en problemas en los que se desconoce un método exacto.Es capaz de suministrar buenas soluciones iniciales al problema, que sirvan como entrada al desarrollo de otros procedimientos.

Problema de corte

Este problema consiste en satisfacer las demandas de unas determinadas piezas, que se deben obtener mediante el corte o partición de un objeto más grande. La asignación generalmente se realiza persiguiendo el objetivo de minimizar los recortes o piezas residuales generadas por el corte y/o conseguir la máxima utilidad.

El algoritmo heurístico utilizado en esta aplicación informática es el algoritmo constructivo o algoritmo Greedy propuesto por Martelo y Toth en 1990.

Las fases para la implementación de este algoritmo son:

Fase 0: Considerar los rectángulos por cortar.

Fase 1: Tomar un rectángulo más pequeño, que el tablero dado (piezas demandadas), es decir, se debe cumplir con la condición lⁱ ≤ L, wⁱ ≤ W.
Ubicar en la parte inferior izquierda.
Hacer corte de guillotina.

Fase 2: Calcular los estimadores de los cuatro tableros resultantes

Resolver el problema de la mochila (knapsack) con variables acotadas

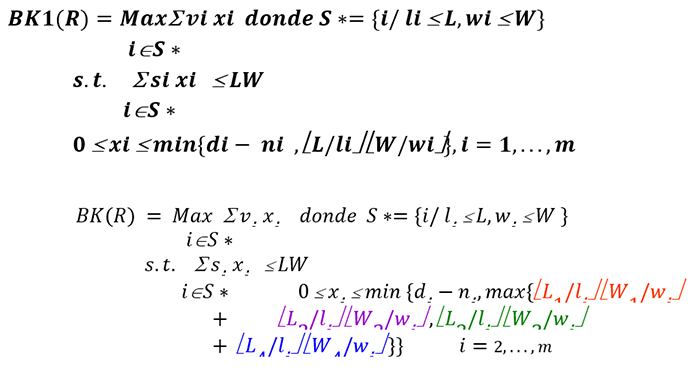
Fase 3: Calcular

Bⁱ = Vⁱ + max{e¹+e², h¹+h²}

Repetir el proceso con todos los cortes demandados y elegir la solución que maximiza la función objetivo.

Este algoritmo realiza la asignación de piezas a ubicar en un tablero para ser cortados.

La interfaz consta de un formulario con los siguientes elementos:

1. Una cuadrícula, donde se cargan los tableros, leídos desde una instancia del archivo de texto seleccionado.
   
2. Se define la instancia como el conjunto de problemas específicos a resolver. (Vicentini & Puddu, 2008)
   
3. Una cuadrícula, donde se ubican las piezas y sus dimensiones a ser ubicadas en el tablero, también leídos desde el tablero.
   
4. Un área de texto donde se muestran los resultados generados por el proceso de optimización.
   
5. Tres botones:
   a. Leer instancias: Lee un archivo de texto que contiene los parámetros a utilizar en el proceso.
   b. Resolver: Aplica el procedimiento de asignaciones. Este proceso genera un archivo de salida donde se encuentran todos los pasos desarrollados y la solución óptima.
   c. Graficar: Genera un gráfico de la ubicación de las piezas.

Interfaz Inicial

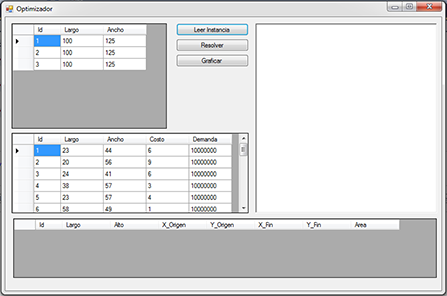
En esta interfaz inicial se muestran los botones de ID, que representa una lectura secuencial de los procedimientos, las lecturas de largo y ancho de la instancia a leer.

También se muestran los anchos y largos de cada uno de los posibles cortes, junto a su costo y demanda de cada pieza, así como las coordenadas de ubicación de las piezas que optimizan la solución.

Procedimiento

Leer la instancia, luego de esto abrirá la siguiente ventana, donde el usuario debe seleccionar una instancia.

Una vez seleccionado el archivo, hacer clic en abrir.

Esto llenará las cuadrículas, a como se muestra a continuación y se procede a hacer clic en el botón de resolver.

Una vez que se encuentra la solución; veremos la siguiente ventana de información.

Se hace clic y a continuación se abre la ventana, donde se asigna un nombre al archivo de salida.

Una vez finalizado el procedimiento, se mostrará el siguiente mensaje.

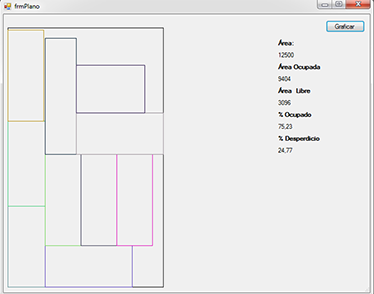
Al hacer clic en graficar, se abre una ventana con un botón graficar, al hacer clic nos mostrará la posible ubicación de las piezas dentro del tablero. Además se muestra el área ocupada, el área libre, el porcentaje ocupado y el porcentaje de desperdicio.

A continuación, se muestra el código fuente de las principales funciones, utilizadas en la aplicación informática:

El botón leer instancia:

El botón resolver:

El código de la función solución:

El código de la función graficar:

Citemos un ejemplo: Supongamos que se quieren elaborar diferentes tipos de tarjetas (invitación, felicitación, presentación, entre otras) para ello se dispone de material que mide 56 por 88 pulgadas. El tamaño de las tarjetas (ancho y largo) y el respectivo costo (en unidades monetarias) se aprecian a continuación:

Al ejecutar la herramienta informática se obtiene el siguiente resultado:

La Mejor Solución
Vertical:
V1: 9 x 78
V2: 47 x 87

Bk (9,78) = 0
S={(6,6) (9,9) (7,10) (7,6) (8,6)}

X3 = 0
X6 = 0
X8 = 10
X9 = 0
X10 = 0

Bk (47,87) = 0

S={(10,14) (10,7) (6,6) (14,14) (20,20) (9,9) (14,10) (7,10) (7,6) (8,6)}

X1 = 24
X2 = 10
X3 = 0
X4 = 0
X5 = 0
X6 = 0
X7 = 0
X8 = 0
X9 = 0
X10 = 0

De los resultados anteriores se observa que la mejor solución es colocar en la parte inferior izquierda una tarjeta de 9 por 9 pulgadas, hacer un corte vertical de dimensiones 9 por 78 pulgadas y de 47 por 48 pulgadas. Luego se obtiene de la parte que mide 9 por 78 pulgadas, diez tarjetas, cuyas medidas son de 7 por 10 pulgadas, y del corte 47 por 87 pulgadas veinte y cuatro tarjetas de 9 por 9 y diez de 14 por 10 pulgadas respectivamente.

En modo gráfico:

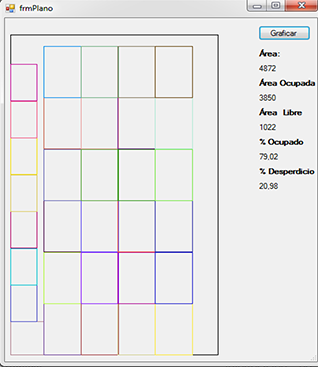
A como se observa, el área total del papel a utilizar es de 4872 pulgadas cuadradas, el área ocupada por las tarjetas a cortar es de 3850 pulgadas cuadradas, es decir hay un 20.98% de desperdicio.

CONCLUSIONES

Si bien, el algoritmo expuesto no obtiene la solución óptima, sin embargo, llega a una solución aproximada, con un ahorro en tiempo de ejecución en el proceso y disminución de costos al tener un menor desperdicio.

La aplicación desarrollada generó nuevos conocimientos, valorando la interrelación de la programación numérica, con las herramientas informáticas para la obtención de una solución a problemas de la vida cotidiana.

A partir del uso de seudocódigos ya existentes, se llegó a crear la aplicación de los algoritmos, siendo muy útil para cálculos de diferentes instancias y no limitada a una en particular.

Se diseñó una aplicación informática, que permitió, un primer acercamiento a la construcción de algoritmos que optimicen recursos, utilizando método de guillotina.

Los algoritmos GRASP son útiles cuando se tiene un gran número de conjunto de datos.

El algoritmo puede aplicarse a diversos sectores de la industria.

Es preciso introducir una fase de mejora, que permita aproximar a una solución más óptima que la obtenida.

BIBLIOGRAFÍA