Incidencia de los estudios sobre reordenamiento genómico en la secuenciación del genoma humano
Impact of genomic reordering studies on human genome sequencing
Wilmer José Palacios López
Facultad Regional Multidisciplinaria de Matagalpa, UNAN-Managua/FAREM-Matagalpa, Nicaragua
https://orcid.org/0000-0002-9783-6271
wilmer.palacios@unan.edu.ni
Fernando José Hernández Gómez
Keiser University, Nicaragua
https://orcid.org/0000-0002-5132-2769
fernando.hernandez@keiseruniversity.edu
Recibido
27/02/2023
Aceptado
21/06/2023
RESUMEN
En este artículo de revisión se muestran los principales aportes de la literatura científica relacionados con el problema SBPR (Sorting Permutations By Prefix Reversals, en español, Ordenamiento de permutaciones con reversión de prefijos) realizados en los últimos 47 años que han servido como base en la secuenciación completa del genoma humano. De hecho, este estudio tiene como propósito describir los principales antecedentes del problema desde sus orígenes hasta su aplicación final en la secuenciación del genoma humano. La metodología utilizada está basada en la revisión documental, la cual permitió construir una matriz y un grafo, en donde se resumen todas las interconexiones bibliográficas posibles. Sin embargo, los principales hallazgos demuestran que los años 90 fueron claves para desarrollar una teoría sólida en cuanto a construcción y verificación en lo que refiere a algoritmos. Finalmente, se brindan las conclusiones y perspectivas a futuro de los principales resultados obtenidos.
PALABRAS CLAVES
Ordenamiento de permutaciones; algoritmos heurísticos; algoritmos metaheurísticos; genoma humano.
ABSTRACT
This review article shows the main contributions of the scientific literature related to the SBPR problem (Sorting Permutations By Prefix Reversals) carried out in the last 47 years that have served as the basis for the complete sequencing of the human genome. In fact, the purpose of this study is to describe the main background of the problem from its origins to its final application in human genome sequencing. The methodology used is based on the documentary review, which allowed the construction of a matrix and a graph, where all possible bibliographic interconnections are summarized. However, the main findings show that the 1990s were key to develop a solid theory in terms of construction and verification of algorithms. Finally, conclusions and future perspectives of the main results obtained are given.
KEYWORDS
Permutation ordering; heuristic algorithms; metaheuristic algorithms; human genome.
INTRODUCCIÓN
En los últimos años, la comunidad científica ha realizado enormes hazañas. Desde el descubrimiento del Bosón de Higgs en julio de 2012, la comprobación de la existencia de las ondas gravitacionales predichas por Einstein en febrero de 2016, el lanzamiento del telescopio espacial James Webb en diciembre de 2021 y finalmente en marzo de 2022 logran secuenciar por primera vez el 100% del genoma humano.1
Todos estos son descubrimientos sorprendentes que han tardado muchos años en dar los resultados esperados. De hecho, todos estos proyectos son trabajos de investigación que han tardado décadas en mostrar resultados o avances significativos. Esa larga espera se debe normalmente a la carencia de recursos técnicos o inclusive a la falta del conocimiento necesario para resolver todos los obstáculos que se interpongan. Este fue el caso del proyecto del genoma humano, cuyos inicios se remontan hace más de 20 años y su particular relación con la teoría de reordenamiento por reversión lo convierten el principal objeto de este artículo.
De hecho, el objetivo principal de este documento es describir la estrecha relación existente entre los resultados finales del proyecto del genoma humano y los orígenes del problema SBPR, haciendo un recorrido exhaustivo por antecedentes y su estado del arte actual, lo cual permitirá comprender los principales nexos entre ambas disciplinas. La capacidad de ordenar eficientemente las permutaciones genómicas mediante la reversión de prefijos ha permitido superar desafíos técnicos y optimizar ciertas tareas en el proceso de secuenciación, allanando el camino hacia la obtención del genoma humano completo.
Además, es importante resaltar que la comprensión de los mecanismos de reordenamiento genómico y su aplicación en la secuenciación no solo ha sido relevante para el proyecto del genoma humano, sino que también ha sentado las bases para investigaciones futuras en genómica comparativa, evolución molecular y biología computacional. El estudio detallado de las interconexiones bibliográficas y los avances teóricos en este campo nos brinda una visión más profunda de cómo el reordenamiento genómico ha influido en el progreso científico y en nuestra comprensión de la complejidad genética.
Antecedentes
Usualmente, cuando se piensa en un acertijo, lo primero que viene a la mente es entretenimiento o agilidad mental. Sin embargo, esto no siempre es así. Muchos problemas matemáticos pueden tener una trascendencia que va mucho más allá de un simple pasatiempo. Este ha sido el caso también del problema SBPR.
Todo inició con Dweighter (1975) y su publicación en la prestigiosa revista American Mathematical Montly sobre un problema2 con el siguiente enunciado (traducido del inglés):
El chef de nuestro local es descuidado y cuando prepara una pila de panqueques, salen de diferentes tamaños. Antes de entregarlos al cliente, de camino a la mesa, los organiza (de modo que el más pequeño se ubique arriba, y así sucesivamente, hasta que el más grande esté abajo) tomando varios de la parte superior y volteándolos por encima. Repitiendo esto (es decir, variando el número de vueltas) tantas veces como sea necesario. Si hay 𝑛 panqueques, ¿cuál es el número máximo de vueltas (en función de 𝑛) que tendré que usar para ordenarlos?. (p. 1010)
Es importante aclarar que no se trata de un problema de ordenamiento en el sentido estricto, puesto que la operación de invertir o dar vuelta a una cierta cantidad de elementos ya está definida. Esto significa que el objetivo real es encontrar una secuencia de ordenamiento que permita realizar las respectivas inversiones a la permutación dada.
Un par de años después Dweighter et al. (1977) mostraron una secuencia de 𝑛 para el caso de maximización.
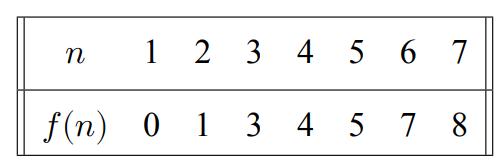
Siendo
![]()
De nuevo, es importante señalar que el planteamiento original sugiere resolver el caso de maximización. Por otro lado, Gates y Papadimitriou (1979) mostraron que es posible ordenar una permutación en 5/3𝑛 inversiones. Adicionalmente, propusieron una nueva variante del problema utilizando signos negativos y positivos para cada elemento, esto también conocido como problema de los panqueques quemados.
De hecho establecieron cotas razonables con el objetivo de acercarse sutilmente a la solución óptima:
![]()
![]()
A pesar del marcado interés de muchos investigadores en problemas combinatorios por su aplicabilidad inmediata en escenarios reales, la siguiente década se caracterizó por una notable inactividad académica y contribuciones menores. Es posible que durante esa época el problema se haya visualizado como un reto o puzzle en lugar de un verdadero problema de investigación. Muchos años después ocurrió lo que para muchos fue el principal punto de inflexión de esta historia. A finales del siglo pasado, Bafna y Pevzner (1996) encontraron una especial relación entre el reordenamiento genómico y cómo este caso particular del problema puede modelar su comportamiento de una forma natural.
Observaron principalmente cómo la distancia entre dos permutaciones aleatorias está relacionada en cierto sentido con su diámetro3. Sin embargo, es importante aclarar que previo a este estudio existieron muchos otros, pero quizás este tuvo una mayor visibilidad y aceptación entre la comunidad.
Como es evidente, a partir de ese momento empezaron a surgir estudios más completos que van desde algoritmos de aproximación hasta la implementación de metaheurísticas que proponían distintos enfoques para encontrar esa secuencia de ordenamiento óptima requerida.
En esta misma línea, Fischer y Ginzinger (2005) construyeron un poderoso algoritmo que representa la primera aproximación polinomial con un radio de 2 unidades. Probablemente, el enorme éxito de esta propuesta se basa en la introducción de dos nuevos conceptos en la literatura: puntos de interrupción y grafo de puntos de interrupción.
Posteriormente, Zhongxi y Tao (2006) idearon una de las primeras propuestas metaheurísticas aplicadas a problemas de reordenamiento genómico. Aunque en realidad hicieron énfasis en la creación de un modelo intente resolver el caso de las permutaciones con signo, muy similar al problema original pero, según ellos, ligeramente más simple. Mostraron mejoras significativas en los tiempos de ejecución en comparación a los resultados obtenidos por Christie (1998), quien propuso un algoritmo de aproximación para el caso general del problema.
Dos años después, Sharmin et al. (2008) desarrollaron una propuesta de aproximación en el cual mostraron algunas mejoras en su radio con (3 − 3𝑟/(𝜋)+𝑟), sin embargo, este fue uno de los tantos intentos por encontrar una solución funcional, pero sin grandes resultados significativos.
A pesar de que el algoritmo dominante seguía siendo el de Fischer y su equipo, Chitturi et al. (2009) desarrollaron una exposición matemática sobre la posibilidad de transformar la idea original de Gates y Papadimitriou (1979) en una serie de casos que pudiera converger hacia una cota superior de 18/11𝑛. De hecho, este planteamiento ha sido aceptado por la comunidad hasta el día de hoy.
Por otro lado, Helmert (1979) desarrolló una propuesta novedosa, aunque injustamente ignorada por muchos autores, llamada heurística de brecha, especialmente diseñada para problemas de planeación y horarios. En realidad, no se brindan muchos detalles sobre su implementación, pero sí sobre los resultados de su funcionamiento.
Algunos años después ocurre lo que para muchos es considerado el segundo punto de inflexión en la historia del problema: Bulteau et al. (2012) demostraron que el problema es NPHard (Nondeterministic Polynomial Time, en español, tiempo polinomial no determinista, se refiere a un tipo de problemas para los cuales encontrar una solución óptima en un tiempo razonable es extremadamente difícil). Esto evidentemente planteó un cambio de mentalidad en la comunidad y a partir de este momento muchos de los esfuerzos estuvieron enfocados en el desarrollo de soluciones heurísticas y metaheurísticas que permitan hacer más manejables grandes instancias del problema y obtener así muy buenos resultados.
En este sentido, SonccoÁlvarez y AyalaRincón (2012) desarrollaron la primera propuesta de algoritmos genéticos conocida después de la demostración. El principal reto en este punto fue modificar el flujo natural del algoritmo genético para intentar adaptarlo al problema. Su impacto fue significativo, ya que mejoró en promedio los resultados de Christie (1998). Otra cosa que es importante resaltar es que han sido los primeros autores en publicar su implementación en un repositorio público.
También, es importante destacar el trabajo de tesis doctoral desarrollado por Bulteau (2013) en donde explican más a fondo los conceptos de base utilizados para demostrar que el problema es NP-Hard. Todas estas son ideas extraídas de campos como el álgebra lineal, la teoría de conjuntos y el análisis combinatorio.
Ese mismo año SonccoÁlvarez y AyalaRincón (2013) mejoraron su idea anterior de tal manera que concibieron un método sistemático para eliminar puntos de interrupción, aunque esta vez analizando más de cerca a las permutaciones con signo. De hecho, este grupo de autores han desarrollado el trabajo más significativo en materia de algoritmos genéticos en los últimos 20 años.
Aunque los algoritmos basados en fenómenos genéticos gozan de una enorme popularidad por su sencillo mecanismo de convergencia y facilidad de implementación, es importante mencionar que existen alternativas muy competitivas como los basados en SI (Swarm Intelligenceen español, Inteligencia de enjambres) tales como: hormigas, abejas, aves, murciélagos, libélulas y demás, cuyos procedimientos se han estandarizado con el paso del tiempo. Con esta base, Al Daoud (2014) propuso una solución basada en una colonia de hormigas que en su defecto necesitan encontrar la secuencia de ordenamiento óptima haciendo uso nuevamente del concepto de puntos de interrupción. Sus resultados, aunque no muy populares, se consideran pioneros por su originalidad.
Ese mismo año SonccoÁlvarez y Ayala-Rincón (2014) presentaron su nuevo avance en materia de algoritmos meméticos, esta vez haciendo un verdadero énfasis al tema de estudio de esta tesis. Posiblemente, esta sea la única propuesta metaheurística directa que se haya aplicado al problema en toda su literatura. De hecho, este enfoque demostró tener resultados más competitivos en comparación con el algoritmo genético estándar e inclusive su versión implementada al utilizar computación paralela.
De forma similar, los siguientes autores han propuesto un verdadero corpus de soluciones heurísticas de las más variadas. En el caso de Dias et al. (2014) diseñaron un marco de trabajo holístico para aproximar soluciones en familias completas de problemas como el de las permutaciones por reversión, llamaron a su algoritmo principal Ventana Corrediza debido a que inicialmente se tiene una estructura de datos que itera y mejora su aproximación hasta el final de la ejecución, sigue una filosofía muy parecida a un algoritmo voraz.
Dentro de este marco, Dias y Dias (2015) presentaron un nuevo punto de vista relacionado con el ordenamiento por inversiones y transposiciones. A pesar de que la relación con el problema de estudio no es muy fuerte, sigue siendo una fuente indirecta de ideas para plantear soluciones con un fundamento más profundo. En este caso, lograron mejorar asintóticamente el factor de aproximación de 3 a 2 unidades.
De hecho, en este grupo de investigadores surgió el gran trabajo de tesis doctoral de Lintzmayer (2016) quien se dio a la tarea de formalizar la notación matemática y a su vez estudiar 45 casos específicos de reordenamiento genómico (entre ellos, el problema de estudio). Adicionalmente, desarrolló una completa composición de algoritmos que mejoran muchas de las aproximaciones conocidas, además de mostrar un nuevo enfoque en el planteamiento de permutaciones con longitud ponderada.
Siempre dentro del mismo círculo de investigadores, Brito et al. (2019) tomaron como base la propuesta anterior de Dias et al. (2014) desarrollando de esta forma una nueva versión de la ventana corrediza y dos nuevas propuestas: búsqueda anticipada y ventana corrediza iterativa. Demostraron que, el primero de estos puede ejecutarse en tiempo lineal a diferencia de la versión anterior y los demás también fueron diseñados para brindar soluciones de calidad para instancias muy grandes.
Es muy importante aclarar que la literatura relacionada con este problema es relativamente corta. Se tomaron en cuenta al menos 18 de los artículos que hacen énfasis tanto en el caso general como en algunos casos particulares por su valioso aporte teórico, y que al mismo tiempo son considerados por la comunidad científica como los estudios más relevantes dentro de toda esta nueva disciplina.
Secuenciación completa del genoma humano
El pasado 31 de marzo de 2022 la revista Science anunció un nuevo hito en la historia de la ciencia moderna: se logró secuenciar completamente por primera vez el genoma humano. Nurk et al. (2022) y su enorme equipo de más de 91 investigadores, confirman que desde el año 2000 se ha logrado explorar el 8 % restante del genoma. Por supuesto, este es el producto de un esfuerzo colectivo y multidisciplinario de distintas áreas del conocimiento, entre las que destaca el estudio de algoritmos eficientes para la transposición de elementos en el ADN (ácido desoxirribonucleico) repetitivo.
La secuenciación completa del genoma humano ha sido de gran relevancia para la ciencia moderna en general y para la biología molecular en particular, ya que proporciona una comprensión más profunda de cómo se forma un organismo individual y a su vez cómo varía no solo entre otros seres humanos, sino también entre diferentes especies. Además, esta secuencia completa permite analizar las diferencias en el ADN entre las personas y determinar si estas variaciones genéticas desempeñan un papel determinante en el desarrollo de enfermedades a corto y largo plazo.
Sin embargo, es interesante observar cómo en este estudio fue necesario el uso de al menos seis estudios distintos sobre reordenamiento y algoritmos de secuenciación, a pesar de ser un carácter más técnico desde el punto de vista biológico. Por tanto, es aquí donde es necesario resaltar la importancia del desarrollo de trabajos como este, ya que sirven como ciencia de apoyo para aquellas contribuciones mucho más grandes y significativas que ayudan a entender más de cerca el verdadero funcionamiento de la naturaleza.
Aunque sus aplicaciones van mucho más allá del ámbito de la biología molecular, sin duda esta es una de las más relevantes, la cual es muy utilizada en la búsqueda de nuevos resultados que ayuden a comprender desde enfermedades como la hemofilia tipo A hasta la evolución de las nuevas especies (ver figura 1).
MATERIALES Y MÉTODOS
Para la elaboración de este artículo se ha realizado una revisión exhaustiva de la literatura relacionada con el problema desde su primera publicación hasta los resultados obtenidos por Nurk et al. (2022).
Las técnicas de recolección de datos utilizadas se centran en la búsqueda y selección de fuentes bibliográficas relevantes, tales como:
- Búsqueda en repositorios y bibliotecas digitales: La gran mayoría de las publicaciones científicas fueron extraídas de revistas especializadas de alto impacto en el área de matemáticas aplicadas y algoritmos computacionales: SIAM (Society For Industrial and Applied Mathematics, en español, Sociedad para las matemáticas Aplicadas e Industriales), Elsevier, Springer, IEEE/ACM (Institute of Electrical and Electronics Engineers/Association for Computing Machinery, en español, Instituto de Ingenieros Eléctricos y Electrónicos/Asociación de Maquinaria Computacional) y arXiv.
- Selección y criterio de inclusión: Se utilizó el criterio de inclusión de búsqueda por palabra clave, tanto en motores de búsqueda online como dentro de cada uno de los documentos de forma digital.
- Análisis textual o de contenido: Se examinó detalladamente cada documento seleccionado para extraer información relevante y a su vez permitiera validar su relación con el estudio principal que se tomó como referencia.
Se ha utilizado una metodología de búsqueda a través de la información bibliográfica de cada trabajo utilizando palabras clave, tales como: algorithm, reversals y prefix. Cada hallazgo se ha dividido en fases, las cuales corresponden a la referencia de uno varios trabajos de la fase anterior. Se toma como referencia principal el estudio de Nurk et al. (2022). Utilizando esta lógica se han filtrado 19 trabajos claves que conectan con el problema inicial en un lapso de 47 años (ver figura 1).
Figura 1 Conexión entre la secuenciación del genoma humano y el origen del problema SBPR
Fuente: Elaboración propia, basada en las fuentes documentales.a los resultados obtenidos por Nurk et al. (2022).
En la figura 2 se puede observar cómo los trabajos con la palabra clave algorithm han destacado con un 42% del total, seguido de reversals cuyo punto más alto se mantuvo en los años 90.
Por otro lado, en la figura 3 se muestra cómo la fase 3 fue la más prolífica en cuanto a publicaciones se refiere. Esto también incluye las décadas de los 90 hasta los avances más recientes en las líneas de algoritmos heurísticos y metaheurísticos.
Figura 2. Bibliografía filtrada por palabra clave
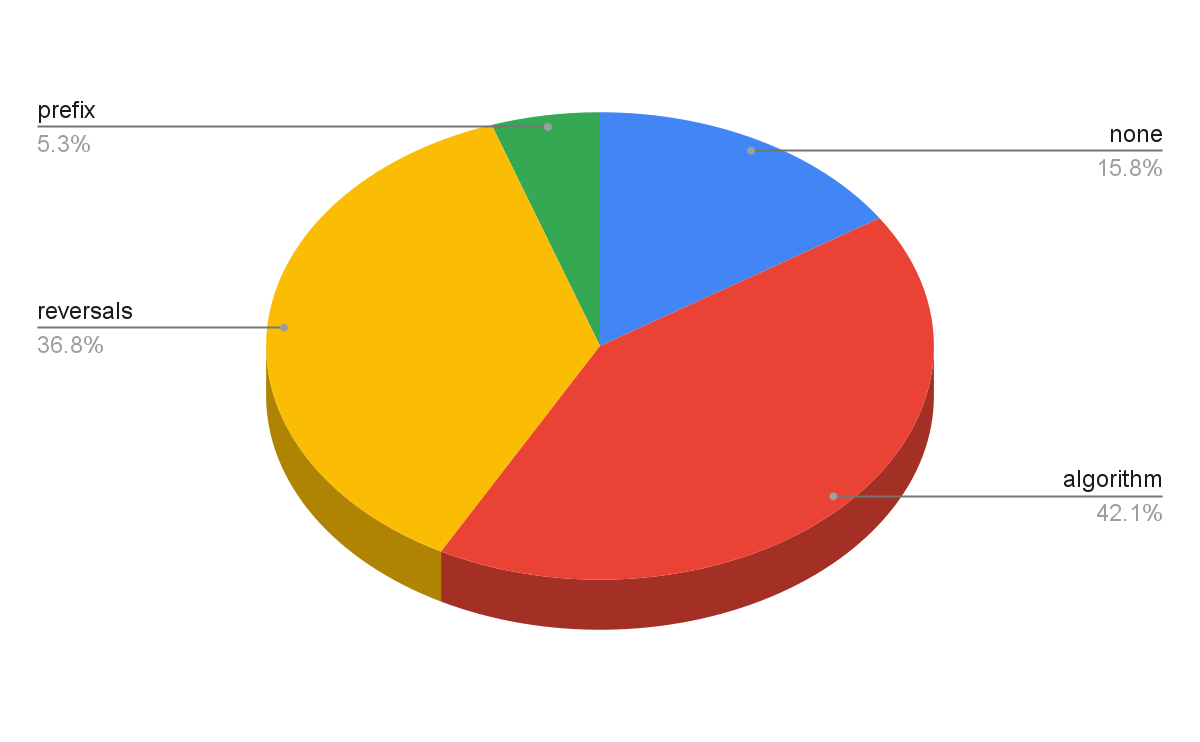
Fuente: Elaboración propia.
Finalmente, en la figura 4 se puede confirmar que el pico más alto de publicaciones sobre este tema ocurrió exactamente a finales de los años 90. Con todo lo anterior se puede afirmar que las líneas de investigación empezaron a converger más seriamente en los inicios de este nuevo milenio. Por supuesto, estos esfuerzos ayudaron a fortalecer los avances técnicos que dieron lugar a uno de los hitos más importantes de la ciencia moderna: la secuenciación completa del genoma humano.
Figura 3: Bibliografía de acuerdo con la fase de investigación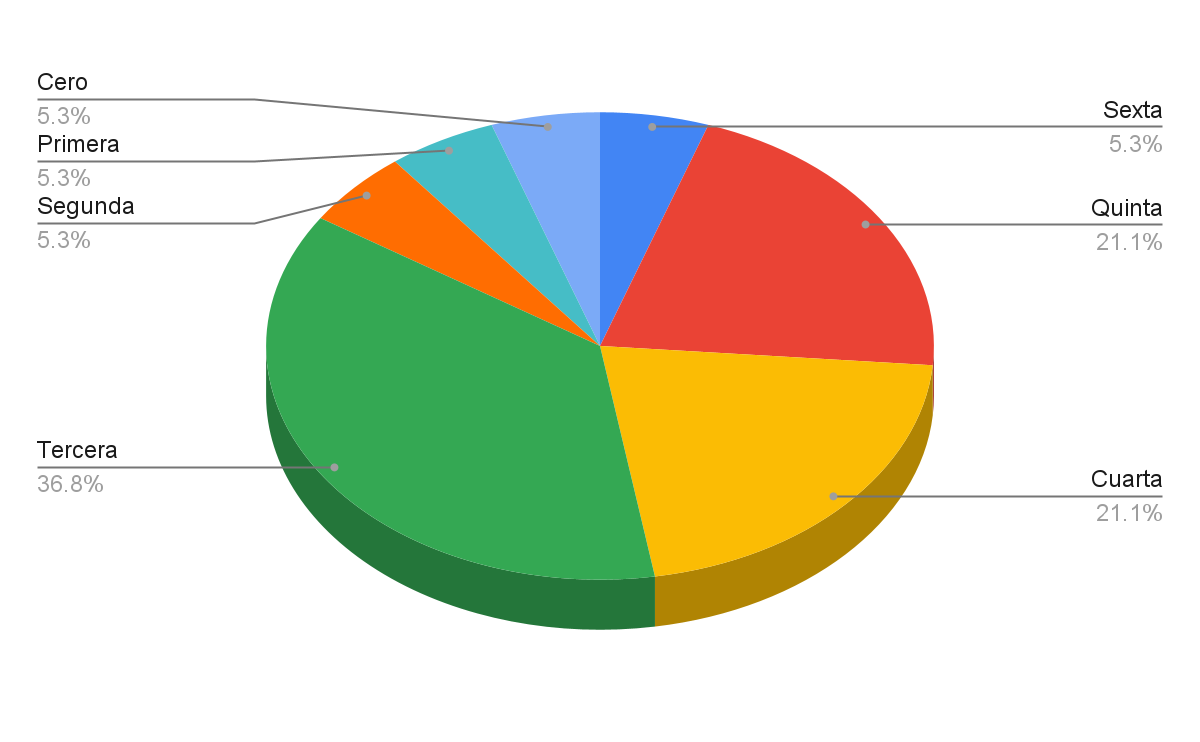
Fuente: Elaboración propia.
Figura 4: Frecuencia de publicaciones por año.
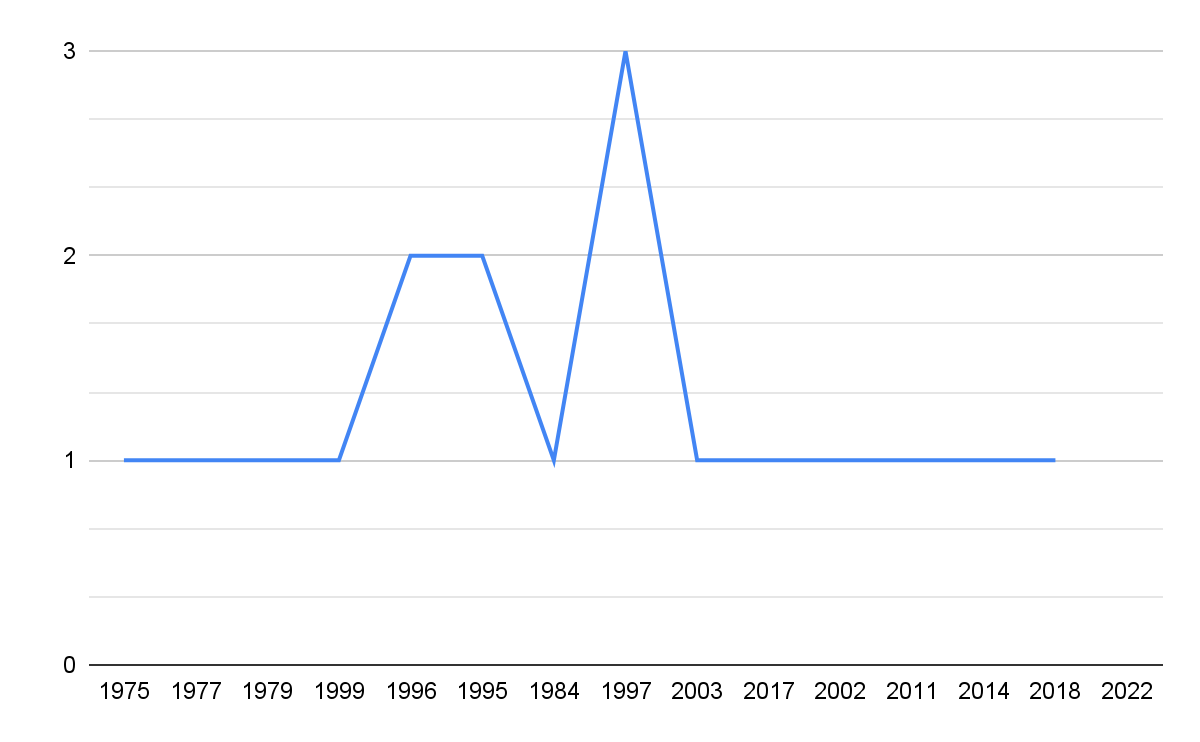
Fuente: Elaboración propia.
La tabla 1 muestra el detalle de todos los trabajos revisados para la elaboración y análisis de este artículo. Esto demuestra nuevamente que todo el conocimiento científico que se ha generado está interconectado y que su carácter multidisciplinar ha permitido abrir y cerrar nuevas líneas de investigación cuyos resultados afectan directamente el quehacer de la sociedad en donde son aplicados y puestos a prueba.
Tabla 1 Matriz de datos que conecta el problema SBPR con la secuenciación del genoma humano
| ID | Fase | Ref | Año | Clave | Titulo | Autores |
|---|---|---|---|---|---|---|
| 1 | Sexta | 0 | 2022 | none | The complete sequence of a human genome | Nurk, S. et al. |
| 2 | Quinta | 1 | 2018 | algorithm | A fast adaptive algorithm for computing whole-genome homology maps | Jain, C., Koren, S., Dilthey, A., Phillippy, A. M., & Aluru, S. |
| 3 | Quinta | 1 | 2014 | algorithm | biobambam: tools for read pair collation based algorithms on BAM files | Tischler, G., & Leonard, S. |
| 4 | Quinta | 1 | 2011 | algorithm | Cactus: Algorithms for genome multiple sequence alignment | Paten, B., Earl, D., Nguyen, N., Diekhans, M., Zerbino, D., & Haussler, D. |
| 5 | Quinta | 1 | 2002 | algorithm | Fast algorithms for large-scale genome alignment and comparison | Delcher, A. L., Phillippy, A., Carlton, J., & Salzberg, S. L. |
| 6 | Cuarta | 2 | 2017 | algorithm | A fast approximate algorithm for mapping long reads to large reference databases | Jain, C., Dilthey, A., Koren, S., Aluru, S., & Phillippy, A. M. |
| 7 | Cuarta | 2 | 2003 | algorithm | Winnowing: local algorithms for document fingerprinting | Schleimer, S., Wilkerson, D. S., & Aiken, A. |
| 8 | Cuarta | 5 | 1997 | algorithm | Algorithms on stings, trees, and sequences: Computer science and computational biology | Gusfield, D. |
| 9 | Cuarta | 5 | 1984 | algorithm | Efficient sequence alignment algorithms | Waterman, M. S. |
| 10 | Tercera | 8 | 1995 | reversals | Sorting by reversals: Genome rearrangements in plant organelles and evolutionary history of X chromosome | Bafna, V., & Pevzner, P. A. |
| 11 | Tercera | 8 | 1996 | reversals | Genome rearrangements and sorting by reversals | Bafna, V., & Pevzner, P. A. |
| 12 | Tercera | 8 | 1996 | reversals | Fast sorting by reversal | Berman, P., & Hannenhalli, S. |
| 13 | Tercera | 8 | 1997 | reversals | Sorting by reversals is difficult | Caprara, A. |
| 14 | Tercera | 8 | 1999 | reversals | Transforming cabbage into turnip: polynomial algorithm for sorting signed permutations by reversals | Hannenhalli, S., & Pevzner, P. A. |
| 15 | Tercera | 8 | 1997 | reversals | Faster and simpler algorithm for sorting signed permutations by reversals | Kaplan, H., Shamir, R., & Tarjan, R. E. |
| 16 | Tercera | 8 | 1995 | reversals | Exact and approximation algorithms for sorting by reversals, with application to genome rearrangement | Kececioglu, J., & Sankoff, D. |
| 17 | Segunda | 11 | 1979 | prefix | Bounds for sorting by prefix reversal | Gates, W. H., & Papadimitriou, C. H. |
| 18 | Primera | 17 | 1977 | none | Amer. Math. Monthly, 82 (4) | Michael R. Garey, David S. Johnson and Shen Lin |
| 19 | Cero | 18 | 1975 | none | Amer. Math. Monthly, 82 (1) | Harry Dweighter |
Fuente: Elaboración propia.
CONCLUSIONES
En este artículo se han mostrado los principales antecedentes que interconectan el problema SBPR con la secuenciación del genoma humano. A lo largo de 47 años se han desarrollado diversas líneas de investigación que han apostado por la resolución de este problema, todas ellas apuntan desde el diseño de algoritmos exactos hasta la implementación de soluciones metaheurísticas.
Luego de realizar un análisis de la bibliografía punto por punto, buscando por palabras clave y asociando cada momento de la línea investigación principal del problema, se han encontrado 19 trabajos que conforman el grafo completo, conexiones bibliográficas entre el origen del problema y la secuenciación del genoma humano.
Es importante resaltar que, a pesar de que la cantidad de publicaciones puede ser significativamente mayor a lo que aquí se muestra; sin embargo, esta es la ruta mínima que permite conectar ambos momentos de su historia. Por supuesto, también se demostró que el momento más prolífico de toda esta línea de investigación ocurrió a finales de los años 90 con los trabajos más influyentes, cuyos resultados impactaron directamente en los avances técnicos en biología molecular de los últimos 20 años.
A futuro se podrían desarrollar más investigaciones que exploren nuevos enfoques híbridos o nuevas estrategias que permitan encontrar soluciones más eficientes y precisas para este tipo de problemas. Asimismo, se podrían inclusive implementar técnicas de aprendizaje automático y análisis de big data para abordar el desafío del reordenamiento genómico y sus aplicaciones de forma directa.
REFERENCIAS BIBLIOGRÁFICAS
Al Daoud, E. (2014). An Improved Ant Colony Algorithm for Genome Rearrangements [Algoritmo mejorado de colonias de hormigas para reordenaciones genómicas]. International Journal of Bioengineering and Life Sciences, 8(5), 768–771.
Baase, S., Van Gelder, A., & García, R. L. E. (2002). Algoritmos computacionales: Introducción al análisis y diseño. Pearson Educación.
Bafna, V., & Pevzner, P. A. (1996). Genome rearrangements and sorting by reversals. [Reordenación del genoma y clasificación por inversiones] SIAM Journal on Computing, 25(2), 272–289. https://doi.org/10.1137/S0097539793250627
Blum, C. (2005). Ant colony optimization: Introduction and recent trends [Optimización mediante colonias de hormigas: Introducción y tendencias recientes] Physics of Life Reviews, 2(4), 353–373. https://doi.org/10.1016/j.plrev.2005.10.001
Bóna, M. (2012). Combinatorics of permutations [Combinatoria de permutaciones]. (2nd ed.). Chapman and Hall/CRC. https://doi.org/10.1201/b12210
Bouzy, B. (2015). An experimental investigation on the pancake problem [Una investigación experimental sobre el problema de los panqueques]. In Computer Games (pp. 30–43). Springer. https://doi.org/10.1007/978-3-319-39402-2_3
Brito, K. L., Oliveira, A. R., Dias, U., & Dias, Z. (2019). Heuristics for the reversal and transposition distance problem [Heurísticas para el problema de la distancia de inversión y transposición]. IEEE/ACM Transactions on Computational Biology and Bioinformatics, 17(1), 2–13. https://doi.org/10.1109/TCBB.2019.2945759
Bulteau, L. (2013). Algorithmic aspects of genome rearrangements [Aspectos algorítmicos de los reordenamientos genómicos]. Université de Nantes.
Bulteau, L., Fertin, G., & Rusu, I. (2012). Pancake flipping is hard [Volterar panqueques es difícil] Proceedings of the 37th International Conference on Mathematical Foundations of Computer Science, 247–258. https://doi.org/10.1016/j.jcss.2015.02.003
Caprara, A., Lancia, G., & Ng, S.-K. (1999). A column-generation based branch-and-bound algorithm for sorting by reversals [Algoritmo branch-and-bound basado en la generación de columnas para la clasificación por inversiones] (Vol. 47). https://doi.org/10.1090/dimacs/047
Chitturi, B., Fahle, W., Meng, Z., Morales, L., Shields, C. O., Sudborough, I. H., & Voit, W. (2009). An (18/11) n upper bound for sorting by prefix reversals [Un límite superior de (18/11) n para la ordenación por inversión de prefijos]. Theoretical Computer Science, 410(36), 3372–3390. https://doi.org/10.1016/j.tcs.2008.04.045
Christie, D. A. (1998). A 3/2-approximation algorithm for sorting by reversals. [Algoritmo de aproximación 3/2 para la clasificación por inversiones] Proceedings of the Ninth Annual ACM-SIAM Symposium on Discrete Algorithms, 244–252.
da Silveira, L. A., Soncco-Álvarez, J. L., & Ayala-Rincón, M. (2017). Parallel genetic algorithms with sharing of individuals for sorting unsigned genomes by reversals [Algoritmos genéticos paralelos con compartición de individuos para ordenar genomas sin signo mediante inversiones]. 2017 IEEE Congress on Evolutionary Computation (CEC), 741–748.
da Silveira, L. A., Soncco-Alvarez, J. L., de Lima, T. A., & Ayala-Rincon, M. (2018). Parallel multi-island genetic algorithm for sorting unsigned genomes by reversals [Algoritmo genético paralelo multi-islas para ordenar genomas sin signo por inversiones]. 2018 IEEE. Congress on Evolutionary Computation (CEC), 1–8.
Dias, U., Galvão, G. R., Lintzmayer, C. N., & Dias, Z. (2014). A general heuristic for genome rearrangement problems [Una heurística general para los problemas de reordenación del genoma]. Journal of Bioinformatics and Computational Biology, 12(03), 1450012. https://doi.org/10.1142/S0219720014500127
Dias, Z., & Dias, U. (2015). Sorting by prefix reversals and prefix transpositions [Clasificación por inversión de prefijos y transposición de prefijos]. Discrete Applied Mathematics, 181, 78–89. https://doi.org/10.1016/j.dam.2014.09.004
Dorigo, M., & Blum, C. (2005). Ant colony optimization theory: A survey [Teoría de optimización de colonias de hormigas: Un estudio]. Theoretical Computer Science, 344(2–3), 243–278. https://doi.org/10.1016/j.tcs.2005.05.020
Dorigo, M., Maniezzo, V., & Colorni, A. (1996). Ant system: optimization by a colony of cooperating agents [Sistema de hormigas: optimización mediante una colonia de agentes cooperantes]. IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), 26(1), 29–41. https://doi.org/10.1109/3477.484436
Du, K.-L., & Swamy, M. (2016). Search and Optimization by Metaheuristics: Techniques and Algorithms Inspired by Nature [Búsqueda y Optimización por Metaheurísticas: Técnicas y Algoritmos Inspirados en la Naturaleza]. Birkhäuser. https://doi.org/10.1007/978-3-319-41192-7
Dweighter, H. (1975). American Mathematical Monthly [Boletín Mensual de Matemáticas]. The Mathematical Association of America, 150, 1010.
Dweighter, H., Garey, M. R., Johnson, D. S., & Lin, S. (1977). E2569. The American Mathematical Monthly [Boletín Mensual de Matemáticas], 84(4), 296–296.
Fertin, G., Labarre, A., Rusu, I., Vialette, S., & Tannier, E. (2009). Combinatorics of genome rearrangements [Combinatoria de reordenaciones genómicas]. MIT press.
Fischer, J., & Ginzinger, S. W. (2005). A 2-approximation algorithm for sorting by prefix reversals [Algoritmo de aproximación a 2 para la ordenación por inversión de prefijos]. European Symposium on Algorithms, 415–425. https://doi.org/10.1007/11561071_38
Gates, W. H., & Papadimitriou, C. H. (1979). Bounds for sorting by prefix reversal [Límites para la clasificación por inversión de prefijos]. Discrete Mathematics, 27(1), 47–57. https://doi.org/10.1016/0012-365X(79)90068-2
Helmert, M. (2010). Landmark heuristics for the pancake problem [Heurística de referencia para el problema de los panqueques]. Third Annual Symposium on Combinatorial Search. https://doi.org/10.1609/socs.v1i1.18176
Heydari, M. H., & Sudborough, I. H. (1992). On sorting by prefix reversals and the diameter of pancake networks [Sobre la clasificación por inversión de prefijos y el diámetro de las redes panqueque]. Heinz Nixdorf Symposium at the University of Paderborn, 218–227. https://doi.org/10.1007/3-540-56731-3_21
Kaplan, H., Shamir, R., & Tarjan, R. E. (1997). Faster and simpler algorithm for sorting signed permutations by reversals [Algoritmo más rápido y sencillo para ordenar permutaciones con signo por inversiones]. Proceedings of the First Annual International Conference on Computational Molecular Biology, 163.
Kramer, O. (2017). Genetic algorithms [Algoritmos genéticos]. In Genetic algorithm essentials (pp. 11–19). Springer.
Lintzmayer, C. N. (2016). The Problem of Sorting Permutations by Prefix and Suffix Rearrangements [El problema de ordenar permutaciones mediante reordenamientos de prefijos y sufijos]. PhD thesis, University of Campinas, Institute of Computing, 2016. In English.
Nurk, S., Koren, S., Rhie, A., Rautiainen, M., V. Bzikadze, A., Mikheenko, A., R. Vollger, M., Altemose, N., Uralsky, L., Gershman, A., Aganezov, S., J. Hoyt, S., Diekhans, M., A. Logsdon, G., Alonge, M., E. Antonarakis, S., Borchers, M., G. Bouffard, G., Y. Brooks, S., … M. Phillippy, A. (2022). The complete sequence of a human genome [La secuencia completa del genoma humano]. Science, 376(6588), 44–53. https://doi.org/10.1126/science.abj6987
Sharmin, M., Yeasmin, R., & Hasan, M. (2008). Sorting by Prefix Reversals and Prefix Transpositions with Forward March [Clasificación por inversiones de prefijos y transposiciones de prefijos con marcha adelante]. ArXiv Preprint ArXiv:0812.3933.
Soncco-Álvarez, J. L., Almeida, G. M., Becker, J., & Ayala-Rincon, M. (2013). Parallelization and virtualization of genetic algorithms for sorting permutations by reversals [Paralelización y virtualización de algoritmos genéticos para ordenar permutaciones por inversiones]. 2013 World Congress on Nature and Biologically Inspired Computing, 29–35. https://doi.org/10.1109/NaBIC.2013.6617871
Soncco-Álvarez, J. L., & Ayala-Rincón, M. (2012). A genetic approach with a simple fitness function for sorting unsigned permutations by reversals [Un enfoque genético con una función de adecuación sencilla para ordenar permutaciones sin signo por inversiones]. 2012 7th Colombian Computing Congress (CCC), 1–6. https://doi.org/ 10.1109/ColombianCC.2012.6398025
Soncco-Álvarez, J. L., & Ayala-Rincón, M. (2013). Sorting permutations by reversals through a hybrid genetic algorithm based on breakpoint elimination and exact solutions for signed permutations [Ordenación de permutaciones por inversiones mediante un algoritmo genético híbrido basado en la eliminación de puntos de ruptura y soluciones exactas para permutaciones con signo]. Electronic Notes in Theoretical Computer Science, 292, 119–133. https://doi.org/10.1016/j.entcs.2013.02.009
Soncco-Álvarez, J. L., & Ayala-Rincón, M. (2014). Memetic algorithm for sorting unsigned permutations by reversals [Algoritmo memético para ordenar permutaciones sin signo por inversiones]. 2014 IEEE Congress on Evolutionary Computation (CEC), 2770–2777. https://doi.org/10.1109/CEC.2014.6900398
Zhongxi, M., & Tao, Z. (2006). An improved genetic algorithm for problem of genome rearrangement [Un algoritmo genético mejorado para problemas de reordenación del genoma]. Wuhan University Journal of Natural Sciences, 11(3), 498–502. https://doi.org/10.1007/BF02836651
1 Véase en este artículo: Cómo se logró secuenciar por primera vez al 100% el genoma humano (y qué implicaciones tiene) - BBC News Mundo
2 Por su alusión realizada a los panqueques, también es conocido como el problema de los panqueques o SBPR.
3 Dada una permutación 𝜋 se debe encontrar (𝜋) = 𝑚{𝜍} utilizando operaciones 𝜌(1, 𝑗), de tal forma que 𝜋 = i.
© 2023 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
