Propiedades adicionales del trapecio

Additional trapezoid properties

 

Jony Alexander Rojas Rojas
Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0000-0003-4428-5127
jony.rojas@unan.edu.ni

Armando José Huete Fuentes
Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0009-0003-7874-2354
armando.huete@unan.edu.ni

 

Recibido

28/02/2023

Aceptado

22/06/2023

 

RESUMEN

En libros de texto elaborados en el Proyecto para el Aprendizaje Amigable de la Matemática en Educación Secundaria de Nicaragua (NICAMATE), se presentan los suficientes aspectos teóricos geométricos para realizar un estudio profundo del trapecio, sin embargo, este se muestra limitado al cálculo de área. Por lo cual, este estudio se propone mostrar demostraciones de propiedades geométricas del trapecio valiéndose de la geometría del triángulo y la trigonometría, y proporcionar nuevas propiedades que relacionan los elementos de un trapecio isósceles. Para ello, se combinan el análisis de contenido, los métodos inductivo e hipotético – deductivo y la experiencia docente de los autores. Como resultados se obtienen cuatro nuevas formas de demostración de dos fórmulas conocidas del área de un trapecio y una tercera en función de la longitud de su mediana, la longitud de un lado y el seno del ángulo formado por este y la base mayor. Además, se presentan tres nuevas demostraciones de una fórmula conocida para la longitud de la mediana de un trapecio. También se deducen y demuestran fórmulas no existentes en la literatura de habla hispana, que establecen relaciones entre bases, lados y ángulos basales. Las razones en un triángulo rectángulo y las identidades trigonométricas mostraron ser herramientas útiles en la demostración de propiedades geométricas del trapecio.

 

PALABRAS CLAVES

Trapecio; trapecio isósceles; propiedades geométricas; NICAMATE.

 

ABSTRACT

In textbooks elaborated in the Project for the Friendly Learning of Mathematics in Secondary Education in Nicaragua (NICAMATE), enough geometric theoretical aspects are presented to realize a deep study of the trapezoid, however, this is limited to the calculation of area. Therefore, this study proposes to show demonstrations of geometric properties of the trapezoid using the geometry of the triangle and trigonometry, and to provide new properties that relate the elements of an isosceles trapezoid. For this purpose, content analysis, inductive and hypothetical-deductive methods and the authors’ teaching experience are combined. As results, four new ways of demonstration of two known formulas of the area of a trapezoid and a third one in function of the length of its median, the length of a side and the sine of the angle formed by this one and the major base are obtained. In addition, three new demonstrations of a known formula for the length of the median of a trapezoid are presented. Also, formulas not existing in the Spanish-speaking literature that establish relationships between bases, sides and basal angles are deduced and demonstrated. Ratios in a right triangle and trigonometric identities were shown to be useful tools in the demonstration of geometric properties of the trapezoid.

 

KEYWORDS

Trapezoid; isosceles trapezoid; geometric properties; NICAMATE.

 

INTRODUCCIÓN

 

La geometría es una rama de la matemática que se estructura de forma lógica, donde cada teoría parte de términos primitivos, axiomas y definiciones que al relacionarlos dan paso a la formación de proposiciones que se conocen como teoremas, los cuales deben ser demostrados para ser considerados verdaderos (Moise, 1976, pp. 57-61; Rojo, 1978, p. 208).

En los libros de texto NICAMATE del Ministerio de Educación (MINED) la geometría estudiada en los grados octavo y noveno está basada en el método deductivo y es utilizada la demostración directa para probar teoremas donde se aplican la congruencia y semejanza de triángulos. Cabe señalar que en estas temáticas está la mayoría de las horas del currículo de matemática de secundaria que son destinadas a tratar la demostración. Sin embargo, los triángulos y paralelogramos son las únicas figuras geométricas que son estudiadas a profundidad, relegando al cuadrilátero conocido como trapecio. Aunado a esto, hay una carencia de literatura, al menos de habla hispana, que aborde en profundidad propiedades relacionadas con los elementos del trapecio.

A pesar de esto, al analizar la teoría geométrica desarrollada en los libros de texto de séptimo a noveno grado que representan la cuarta unidad pedagógica de NICAMATE, se aprecia que están los suficientes aspectos teóricos para realizar un estudio deductivo al trapecio. Por lo cual, se plantean los siguientes objetivos:

• Mostrar demostraciones de propiedades geométricas del trapecio valiéndose de la geometría del triángulo y la trigonometría para continuar desarrollando el constructo teórico provisto por la geometría escolar en los textos de NICAMATE.
• Proporcionar nuevas propiedades que relacionan los elementos de un trapecio isósceles con el fin de que se brinden soluciones prácticas a problemas de Geometría Euclidiana Avanzada que requieran del uso de este tipo de cuadriláteros.

 

MATERIALES Y MÉTODOS

 

La realización del presente estudio se enmarca en una metodología que combina el análisis de contenido, los métodos inductivo e hipotético – deductivo y la experiencia docente de los autores mediante lo siguiente:

• El análisis de contenido (Noguero, 2002) se usó para la revisión de trabajos que tienen objetivos similares, pero que giran en torno a otro objeto matemático: el cuadrado (Orozco y Cisneros, 2022a), rectángulo y triángulo equilátero (Orozco y Cisneros, 2022b) y el rombo (Orozco y Cisneros, 2022c). Este análisis permite identificar categorías de relaciones entre los elementos de un trapecio (lado, diagonal, bases, mediana, altura y área) que orientan la búsqueda de nuevas fórmulas y demostraciones.

• Por medio del método inductivo (Abreu, 2014) se observó y experimentó con casos concretos que permitieron identificar regularidades, las cuales dieron origen a la formulación de posibles relaciones entre los elementos de un trapecio o más concretamente a nuevas fórmulas de dependencia entre ellos.

• El método hipotético – deductivo permitió mantener un razonamiento sistemático y crítico basado en proposiciones hipotéticas sobre relaciones existentes entre los elementos de un trapecio (Newman, 2006), lo cual dio origen al acto científico propio de los matemáticos, la demostración de cada una de las fórmulas que se presentan en el estudio.

• El método de demostración empleado es el directo o condicional, el cual Suppes y Hill (1994) lo plantean de la siguiente manera: “Si es posible deducir una proposición  de otra proposición  y un conjunto de premisas, entonces se puede deducir solo del conjunto de premisas la proposición condicional ” (p.133).

• Otro elemento importante que contribuye a la realización de la investigación es la experiencia de los autores como docentes de los cursos de Geometría Euclidiana, Geometría analítica y Trigonometría que se imparten en las carreras de Matemática y Física-Matemática de la Facultad de Educación e Idiomas de la UNAN-Managua. Dictar en más de una vez dichos cursos, observar las principales dificultades del estudiantado en el aprendizaje de la Geometría y la experimentación constante en el aula de clase hace que, con el tiempo, se haya ido aprendiendo formas de demostración que sean constructivas, que usen resultados ampliamente conocidos por el estudiantado de educación secundaria y que explote la parte visual y espacial de la Geometría.

• Por último, se emplearon aspectos teóricos ampliamente conocidos de trigonometría y Geometría Euclidiana como: congruencia y semejanza de triángulos, así como las identidades trigonométricas los cuales contribuyeron en brindar los argumentos teóricos que sustentan la validez de cada teorema presentado.

 

RESULTADOS Y DISCUSIÓN

 

En esta sección se exponen una serie de teoremas que son el resultado de la implementación del proceso descrito en el apartado anterior. En la redacción de cada teorema y su demostración se mantuvo un lenguaje matemático sencillo y se utilizaron los libros de texto NICAMATE como referencias, todo ello con el propósito de que cualquier lector con grado preuniversitario logre la comprensión de estos.

Teorema 1. La mediana de un trapecio es paralela a cada una de sus bases.

Demostración. Se presentan dos demostraciones para este teorema. Para la primera, considérese el trapecio (Barnett, 1991, p. 85) ABCD con  y mediana  de la Figura 1.

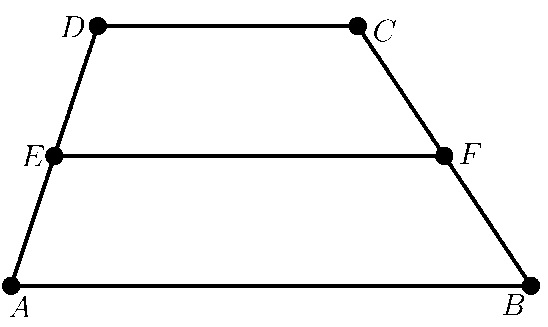
Figura 1. Trapecio con mediana

De la definición de mediana se deduce que,

y al ser , del recíproco del Teorema de Tales (Pérez, 2014, p. 210), resulta

Para la segunda demostración, considérese el trapecio ABCD con  y mediana  de la Figura 2, donde por construcción  es el punto de intersección de las prolongaciones de los lados de este.

Figura 2. Trapecio con mediana y prolongación de sus lados

Por la igualdad de las medidas de ángulos correspondientes formados por dos rectas paralelas y una transversal (Huete et al., 2019, p. 94), resulta

Basado en las igualdades anteriores y la aplicación del criterio de semejanza AA (García et al., 2019, p. 97) se llega a

Por la definición de semejanza de triángulos (García et al., 2019, p. 96), se establece que

Por la igualdad anterior, suma de segmentos, definición de mediana de un trapecio y suma de fracciones, se tiene que

“Restando” 1 “en ambos miembros de "" se obtiene que”

 

de lo cual

así por resta de segmentos se tiene que

De las igualdades

se deduce que

Por la igualdad anterior,  y la aplicación del criterio de semejanza LAL (García et al., 2019, p. 99), se tiene que

De la definición de semejanza se deduce que

Luego, por ser  y  ángulos correspondientes con igual medida, entonces las líneas cortadas por la transversal son paralelas (Huete et al., 2019, p. 98), esto es

Por la definición de trapecio y dado que , se concluye que

Teorema 2. La longitud de la mediana de un trapecio es igual a la semisuma de las longitudes de sus bases (Barnett, 1991, p. 95).

Demostración. Se presentan tres demostraciones para este teorema. Para la primera, considérese el trapecio ABCD con  y mediana  de la Figura 3, donde G y H son el pie de la altura trazada desde D y C, respectivamente.

Figura 3. Trapecio con mediana  y alturas  y

Por el Teorema 1 y el teorema fundamental de la proporcionalidad (García et al., 2019, p. 110),

Dado que   son alturas  (Teorema 1), se deduce que

Así por el postulado de la suma de segmentos (Velásquez et al., 2019, p. 127),

Por las igualdades

se tiene que

Así por la cadena de igualdades anterior, se concluye que

De esta forma queda demostrado que, en todo trapecio, la longitud de su mediana queda determinada por la semisuma de las longitudes de sus bases.

Para la segunda demostración, considérese el trapecio ABCD con  y mediana  de la Figura 4, donde por construcción A' y F' son los puntos respectivos donde las prolongaciones de  y  interceptan a la paralela a  que pasa por B. De lo anterior, se tiene que

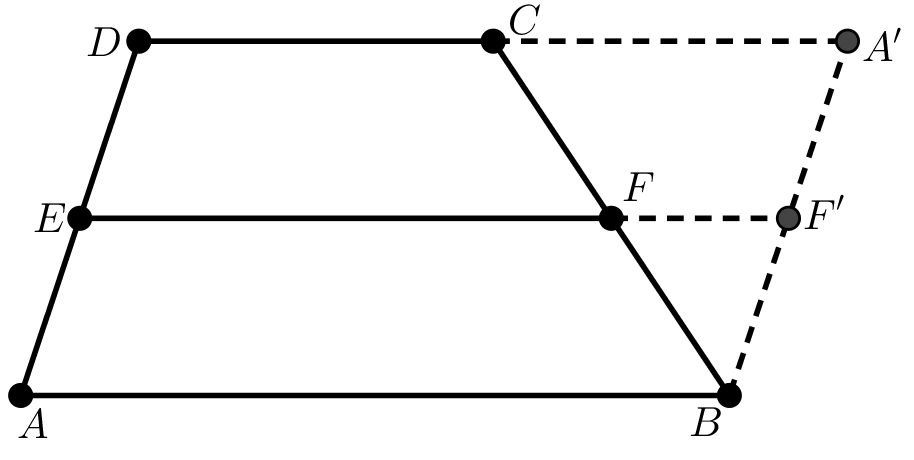
Figura 4. Trapecio con mediana  y base menor prolongada

Por el Teorema 1, , por lo cual

Del paralelismo entre   , se obtiene que

Luego, por la igualdad de las medidas de ángulos correspondientes formados por dos rectas paralelas y una transversal, resulta

Basado en las dos igualdades anteriores y la aplicación del criterio de semejanza AA, se llega a

Por las definiciones de semejanza de triángulos y mediana de un trapecio, resulta

por lo que

.

Dado que , se deduce que

 

El cuadrilátero ABA'D es un paralelogramo, dado que . Luego, se tiene

De la cadena de igualdades anterior, se concluye que

Para la tercera demostración, considérese la Figura 2. Por la igualdad de las medidas de ángulos correspondientes formados por dos rectas paralelas y una transversal, resulta

Basado en las igualdades anteriores y la aplicación del criterio de semejanza AA, se llega a

Por la definición de semejanza de triángulos, resulta

Sumando miembro a miembro las dos igualdades anteriores, se obtiene

De la cadena de igualdades anterior, EH = ED + HD y AD = 2ED, se tiene

Así se concluye que

Teorema 3. El área de un trapecio está dada por el semiproducto de su altura y la suma de las longitudes de sus bases (Barnett, 1991, p. 199).

Demostración. Se presentan 3 demostraciones diferentes para este teorema. Para la primera demostración, considérese el trapecio ABCD con  y altura  de la Figura 5, donde por construcción A' es el punto donde la prolongación de  intercepta a la paralela a  que pasa por B. De lo anterior, se tiene que

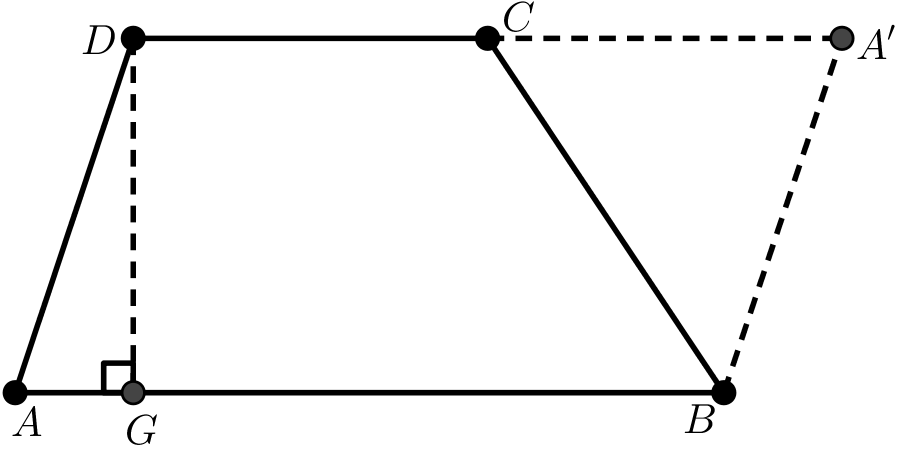
Figura 5. Trapecio con base menor prolongada

Dado que , entonces . Al ser paralelos  con  y  con , resulta que el cuadrilátero ABA'D es un paralelogramo. Luego, por las fórmulas para el área de un paralelogramo y un triángulo, se obtiene que

Como A'C = AB - DC , entonces

Así se concluye que

Para la segunda, considérese el trapecio ABCD de la Figura 6.

Figura 6. Trapecio dividido en tres regiones

Note que el trapecio se descompone en dos triángulos rectángulos (∆DGA y ∆CHB) y un rectángulo (DCHG). Luego, por las fórmulas de área de un triángulo y un rectángulo (Velásquez et al., 2019, pp. 153-154),

 

Para la tercera demostración, considérese el trapecio ABCD con  y mediana  de la Figura 7, donde G es el pie de la altura trazada desde D.

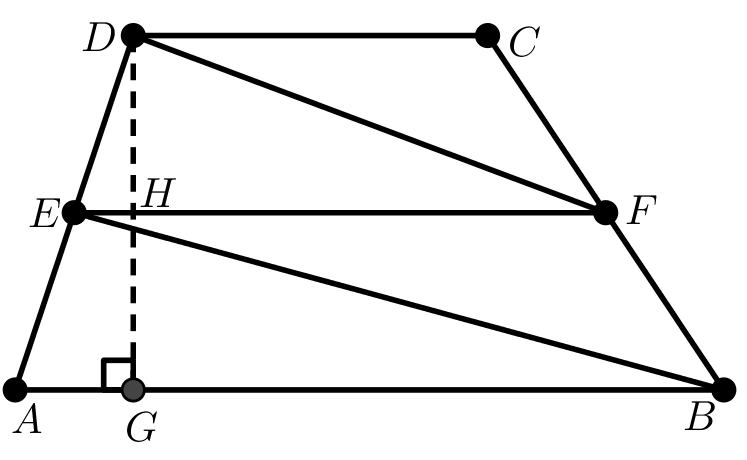
Figura 7. Trapecio dividido en cuatro regiones triangulares

Note que al trazar DF y EB, el trapecio se descompone en cuatro triángulos.

Por el Teorema 1 se sabe que , así DEH ≅∠ DAG por ser ángulos correspondientes entre paralelas (Huete et al., 2019, p. 94) y además ∠EDH≅∠ADG, por lo cual ∆EDH~∆ADG (García et al., 2019, p. 97). Luego, por definición de semejanza de triángulos (García et al., 2019, p. 96) y propiedades de la igualdad

Dado que la distancia entre dos rectas paralelas es la misma (Velásquez et al., 2019) los triángulos ∆DEF y ∆FCD tienen altura 1/2 DG. Similarmente, como HG=1/2 DG, resulta que la altura de los triángulos ∆AEB y ∆BFE también es 1/2 DG. Esto deja en evidencia que los cuatro triángulos en que se descompone el trapecio tienen como altura 1/2 DG.

De la fórmula del área de un triángulo y el Teorema 2, se deduce

 

Teorema 4. El área de un trapecio es el producto de su altura y la longitud de su mediana (Barnett, 1991, p. 199).

Demostración. Por la aplicación de los Teoremas 2 y 3 en la Figura 7, resulta que

Área = DG∙EF.

Teorema 5. El área de un trapecio es el producto de su mediana, la longitud de un lado y el seno del ángulo formado por este y la base mayor.

Demostración. or la aplicación del Teorema 4 y la definición del seno (Aráuz et al., 2019, p. 81) en la Figura 7, se obtiene que Área=DG∙EF y sen A=DG/AD, respectivamente. De lo cual se deduce que

Área = EF ∙ AD ∙ sen A. .

Teorema 6. En un trapecio isósceles la diferencia entre la base mayor y la menor es el doble del producto de la longitud de uno de sus lados y el coseno del ángulo formado por este y la base mayor.

Demostración. Considérese el trapecio isósceles ABCD con AD = BC de la Figura 8, donde G y H son el pie de la altura trazada desde D y C, respectivamente.

Figura 8. Trapecio isósceles

Observe que ∆DGA y ∆CHB son triángulos rectángulos con DG=CH, así del teorema de congruencia hipotenusa-cateto (Huete et al., 2019, p. 122), se obtiene que ∆DGA ≅ ∆CHB, por lo cual

AG=HB.

Al aplicar el teorema de Pitágoras (García et al., 2019, p. 125) y la definición de la razón seno en el ∆DGA, se tiene que AG² = AD² - AD² sen² θ. Luego, de la propiedad distributiva y las identidades pitagóricas, resulta AG₂ = AD²cos² θ. Al extraer raíz cuadrada en ambos miembros de la última igualdad, se obtiene

AG = AD ∙ cos θ.

Nótese en la Figura 8, que la diferencia entre las bases mayor y menor es la suma AG+HB, así de

AG = HB y AG = AD ∙ cos θ, se concluye

Teorema 7. En un trapecio isósceles el producto de las longitudes de la base mayor y la menor es igual a la diferencia entre el cuadrado de la longitud de una diagonal y el cuadrado de la longitud de uno de sus lados.

Demostración. Considérese el trapecio isósceles ABCD con AD=BC de la Figura 9

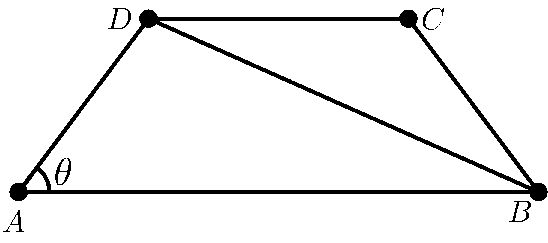
Figura 9. Trapecio isósceles con una de sus diagonales

Considérese la diagonal , así al aplicar la ley del coseno (Araúz, 2019, p.132) al ∆ABD se tiene BD² = AD² + AB² - 2AD ∙ AB ∙ cos θ. Por la transposición de términos, la propiedad distributiva y la aplicación del Teorema 6, resulta

El resultado obtenido es el mismo para la otra diagonal, ya que al ser AD=BC, ∡A=∡B y AB=BA, entonces ∆DAB≅∆CBA. De la congruencia se deduce que BD=AC.

Teorema 8. En un trapecio isósceles el producto de las longitudes de la base mayor y la menor es igual a la diferencia entre el cuadrado de la longitud de su mediana y el cuadrado del producto de la longitud de uno de sus lados y el coseno del ángulo formado por este y la base mayor.

Demostración. Considérese el trapecio isósceles ABCD con AD=BC y mediana de la Figura 10.

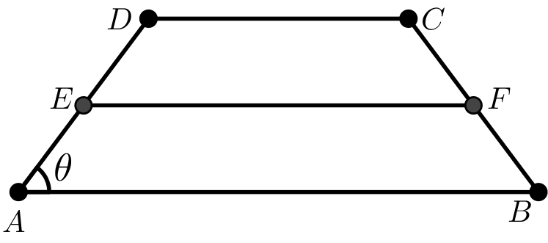
Figura 10. Mediana en un trapecio isósceles

Por el Teorema 6, las propiedades de la igualdad y el Teorema 2, se tiene que

Al elevar al cuadrado ambos miembros de la igualdad anterior, transponer términos y aplicar la propiedad distributiva, resulta

Por el Teorema 6, se obtiene

Los resultados obtenidos en el presente estudio muestran que los libros de texto NICAMATE cuentan con la base teórica necesaria para que estudiantes preuniversitarios puedan demostrar la validez de enunciados (teoremas) sobre figuras geométricas que no forman parte del currículo de la asignatura de matemática. Los siguientes aspectos teóricos permitieron argumentar la veracidad de cada una de las proposiciones expuestas:

• Definiciones de congruencia y semejanza de triángulos.
• Definición de la razón seno de un ángulo agudo.
• Criterios de congruencia: Lado-Ángulo-Lado, Hipotenusa-Cateto.
• Criterios de semejanza de triángulos: Ángulo-Ángulo, Lado-Ángulo-Lado.
• Recíproco del teorema de Tales.
• Teorema de Pitágoras.
• Ley del coseno.
• Identidad Pitagórica que relaciona a las razones trigonométricas seno y coseno.
• Condiciones que garantizan paralelismo y propiedades sobre ángulos formados por dos rectas paralelas y una transversal.
• Teorema fundamental de la proporcionalidad.
• Propiedades de la igualdad.

De la lista anterior, resulta evidente que al estudiar propiedades de Geometría Euclidiana avanzada los tópicos referidos a la geometría del triángulo asumen un papel relevante, ya que para establecer la veracidad de las proposiciones estudiadas se recurre tanto a la semejanza y congruencia de triángulos como a trigonometría plana.

Es importante señalar que, los aspectos teóricos geométricos son suficientes, en el sentido de que no es necesario ir más allá de los contenidos desarrollados en los libros de séptimo a noveno (como se expresó en la introducción), sin embargo, para analizar posibles relaciones que involucraran los ángulos internos de esta figura geométrica se vio la necesidad de auxiliarse de algunos resultados de trigonometría.

 

CONCLUSIONES

 

El presente estudio permitió, proveer cuatro nuevas formas de demostración de dos fórmulas conocidas del área de un trapecio y otra fórmula en función de la longitud de la mediana y las longitudes de las bases, así como tres nuevas demostraciones de una fórmula conocida para la longitud de la mediana de un trapecio. También se deducen y demuestran fórmulas no existentes en la literatura que establecen relaciones entre:

• Bases, lados y ángulos basales de un trapecio isósceles.
• Bases, diagonales y lados de un trapecio isósceles.
• Bases, mediana, ángulo basal y los lados de este.

Para la demostración de las fórmulas se emplearon herramientas propias de la trigonometría como lo son las razones en un triángulo rectángulo y las identidades trigonométricas, mostrando así la relación existente entre distintas ramas de la matemática, en este caso, la geometría con la trigonometría.

Por otra parte, los textos de Geometría Elemental en su mayoría solamente presentan a un trapecio como un cuadrilátero que tiene dos lados paralelos y se limitan a presentar una fórmula para calcular el área de la región que limita a partir de conocer las longitudes de sus bases y la de su altura, sin embargo, al pensar en el trapecio como una figura geométrica de cuatro lados se puede hablar de sus ángulos interiores, diagonales, puntos medios de sus lados y mediana, lo que permite analizar maneras de reescribir fórmulas conocidas en muchos libros de matemática en función de estos, tal es el caso de la fórmula del área.

 

REFERENCIAS BIBLIOGRÁFICAS