Plan de Pizarra como metodología activa del aprendizaje significativo y amigable en Matemáticas para la educación secundaria en Nicaragua
Blackboard Plan as an active methodology for meaningful and friendly learning in Mathematics for secondary education in Nicaragua
Rigoberto Francisco Jarquín Matamoro
Docente de Facultad Regional Multidisciplinaria de Mataglapa, UNAN-Managua/FAREM-Matagalpa, Nicaragua
https://orcid.org/0000-0002-8280-0823
rigoberto.jarquin@unan.edu.ni
Recibido
13/02/2023
Aceptado
27/03/2023
RESUMEN
El presente artículo tiene como objetivo abordar la estructura del plan de pizarra y la mejor manera de evaluar la clase, dado que, es una metodología activa que implementa el Ministerio de educación (MINED) de Nicaragua en conjunto con el programa NICAMATE, desde el año 2019 con el objetivo de mejorar el rendimiento académico de Matemáticas en secundaria, promover su didáctica ejecutando actividades educativas de acuerdo al curriculum adecuado para dicha disciplina, a la vez como un modelo de planeamiento didáctico para el docente fomentando el aprendizaje significativo desde la aplicación de los conocimientos básicos en diversas situaciones y amigables por la manera de jerarquizar los contenidos que son conceptuales, procedimentales, esenciales y aplicativo con cierto grado de complejidad en sus ejercicios y problemas. Este artículo brinda una base teórica en cuanto a la metodología, recursos didácticos, apreciación de la evaluación formativa, gradualidad de los contenidos y la valoración de los aprendizajes, formando la concepción de las matemáticas amigables. Se aplicó la técnica de la observación y prueba objetiva para la recolección de información, se usó el método estadístico probabilístico para el cálculo de la muestra para la aplicación de la prueba, y usando el método teórico – científico, bajo un enfoque positivista. El principal resultado demuestra que los estudiantes presentaron dominio de los contenidos y que el impacto de esta metodología favorece a su aprendizaje.
PALABRAS CLAVES
Metodología; aprendizaje significativo; matemáticas amigables; evaluación.
ABSTRACT
This article aims to address the structure of the blackboard plan and the best way to evaluate the class, given that, it is an active methodology implemented by the Ministry of Education (MINED) of Nicaragua in conjunction with the NICAMATE program, since 2019 with the aim of improving the academic performance of Mathematics in secondary education, promote its didactics by executing educational activities according to the appropriate curriculum for this discipline, as well as a didactic planning model for the teacher promoting meaningful learning from the application of basic knowledge in various situations and friendly by the way of hierarchizing the contents that are conceptual, procedural, essential and applicative with a certain degree of complexity in their exercises and problems. This article provides a theoretical basis in terms of methodology, didactic resources, appreciation of formative evaluation, content gradualism and learning assessment, forming the conception of friendly mathematics. The technique of observation and objective test was applied for the collection of information, the probabilistic statistical method was used to calculate the sample for the application of the test, and using the theoretical-scientific method, under a positivist approach. The main result shows that the students showed mastery of the contents and that the impact of this methodology favors their learning.
KEYWORDS
Methodology; meaningful learning; mathematics friendly; evaluation.
INTRODUCCIÓN
La educación secundaria en Nicaragua a través del Ministerio de Educación (MINED), se ha preocupado continuamente en fortalecer el proceso de enseñanza - aprendizaje, pero especialmente centrándose en el aprendizaje significativo en el estudiante en la asignatura de matemáticas enmarcándose a que, si el estudiante comprende la clase, le gustará matemáticas.
La principal problemática se presenta en la educación secundaria, cuando durante muchos años ha existido la dificultad de los estudiantes en aprender matemáticas, en el planeamiento didáctico, los bajos rendimientos académicos, la reprobación de la clase, la repetición de grados y la nivelación de contenidos. Por ello, en el año 2019 el MINED en conjunto con NICAMATE1 se puso en marcha el proyecto para el Aprendizaje Amigable de Matemática en educación secundaria, que tiene como objetivos fundamentales: mejorar el rendimiento académico de matemática en educación secundaria y promover la cooperación mutua en cuanto a la didáctica de matemática a nivel regional. Estos objetivos generan pautas para vencer los estereotipos como que las matemáticas son difíciles, no se comprenden, entre otros, que han hecho que esta asignatura no sea una de las favoritas por los estudiantes.
Al hacer mención a la importancia de las matemáticas, Matamoros (2021) expone que:
Reside en una respuesta sencilla “la aplicabilidad” en lo que se hace y crea, puesto es vital para encontrar el razonamiento y la organización de maneras para entender el mundo, sin enfrascarse en un mundo cuadrado y no es por exactitud, sino más bien por las aproximaciones que se pueden lograr, consecuente a esto, la didáctica de la matemática avanza rompiendo esquematizaciones y paradigmas que han creado los mismos docentes y que ahora es trabajo de ellos mismos hacer de las matemáticas amigables. (p.32)
Desde los objetivos del programa mejorar el rendimiento académico es fundamental, puesto este es el resumen de los esfuerzos y estrategias que el docente emplea en el aula para lograr cumplir las competencias de grados, eje transversal y los indicadores de logros de manera eficaz y que el estudiante sea capaz de aplicar esos conocimientos en su propio contexto.
Hacer que las matemáticas sean amigables facilita que el estudiante pueda comprender de manera asertiva los conocimientos que se le presentan, y este programa lo hace posible a través de una forma jerárquica, partiendo de lo más sencillo a lo más complejo en un tiempo de 45 minutos fomentando el aprendizaje activo en todo momento. Según este proyecto, supone un cambio en las estructuras mentales del aprendizaje en los estudiantes que se produce a través del análisis, comprensión, elaboración y asimilación de las diversas situaciones e informaciones propuestas en las clases. De esta forma, “el estudiante no constituye un agente pasivo, que se limita a escuchar la clase tomando notas y ocasionalmente plantear preguntas” (MINED, 2019a, p.3).
Lo anterior hace inferencia que el estudiante está activo en toda la clase realizando preguntas, pasando a la pizarra, ejemplificando con situaciones aplicadas a su contexto y no como oyente, donde el docente es el único emisor, sino que los papeles de emisor y receptor pueden permutar.
El modelo del plan pizarra en matemáticas desde su estructura constituye una importante metodología continua de pasos que son congruentes a los momentos del planeamiento didáctico (actividades iniciales, desarrollo, culminación y evaluación), que se desarrollan en el aula de clases en un periodo de 45 minutos usando como su nombre lo dice la pizarra donde MINED (2019a), lo define como:
El medio o recurso didáctico clásico utilizado por casi todos los docentes y es el único que tiene asegurada su existencia en el aula. Constituye un medio operativo de fácil utilización por parte del docente y adecuadamente utilizada facilita el proceso de aprendizaje en el aula. (p.3)
El actuar de este medio o recurso didáctico inicia desde una división de la pizarra en dos columnas, es decir, a la mitad ubicando cada elemento o momentos del plan según el lado correspondiente. Sin embargo, puede tomarse que el plan de pizarra es una parte del planeamiento didáctico que el docente traslada al pizarrón durante el desarrollo de la clase.
Para el programa de NICAMATE en conjunto con el MINED, las funciones didácticas que tiene la pizarra al desarrollar la clase son:
Esquema 1: Funciones didácticas de la pizarra
Fuente: Manual interactivo del plan pizarra, MINED (2019a) y modificado por el autor.
Las funciones anteriores constituyen una parte esencial de lo que se debe tomar en cuenta al desarrollar la clase, pero se corresponde con el eliminar la concepción de que únicamente se use marcador y pizarra, esto recae en como el docente logre usar las estrategias didácticas para adecuar la metodología del plan pizarra respetando cada momento. Cada función persigue el aprendizaje activo, el cual “no es posible aprender por otra persona, sino cada persona tiene que aprender por sí misma, experimentando, resolviendo para generar un enlace con la aplicación del conocimiento previo o enlazando con los cambios conceptuales ya creados” (Huber, 2008, p.9).
Por consiguiente, el aprendizaje activo se logra induciendo a pensar al estudiante, que este genere ideas de cómo resolver un problema, que se le plantee con el conocimiento que tiene actualmente y que pueda realizar o plantear la solución. Siendo esto la base de la metodología del proyecto.
La siguiente figura muestra la estructura que debe tener el plan de pizarra, es decir, que en el planeamiento docente se debe reflejar una estructura igual a la mostrada y la que debe estar plasmada en el pizarrón.
Figura 1Estructura del plan de pizarra
Fuente: Manual interactivo del plan de pizarra, MINED (2019a, p. 4)
La figura anterior muestra el cómo debe estar estructurada la pizarra, los pasos a seguir, que son los momentos de la clase, no se desvincula de los momentos ya conocidos como: actividades iniciales, de desarrollo, finales y de evaluación, sino que están integrados en él. Si bien se observa no se escribe el indicador de logro, ni las competencias de grado, ni eje transversal, estos se pueden explican de forma oral o se mencionan al iniciar la explicación del docente en el problema inicial, pero deben estar plasmados en los datos generales del plan de clases, como se muestran en los ejemplos que están al final del articulo como anexos.
Cada aspecto del plan de pizarra está dentro de las actividades del planeamiento que se maneja con las demás asignaturas en los que se pueden agrupar dentro de las actividades iniciales está el problema inicial (P)¸ en las actividades de desarrollo está la solución(S), conclusión(C) y ejemplo (Ej), en las finales esta la ejercitación(E); en las de evaluación es involucrar todo el proceso formativo del desarrollo de la clase y que los estudiantes resuelvan en su cuaderno primeramente los ejercicios planteados; luego exponga en la pizarra la solución final. Cabe señalar, que deben de tomarse en cuenta el tiempo sugerido, pero esto no implica que siempre será la misma distribución, estos dependerán de cada contenido y del docente, sin embargo, el modelo del plan de pizarra exige que se deben cumplir lo antes sugerido.
El plan de pizarra se fundamenta en ciertos materiales didácticos para poder lograr el aprendizaje perseguido entre ellos MINED (2019b):
- Libro de texto para el estudiante: este libro debe tenerlo cada uno de los estudiantes durante la clase en el momento de desarrollo, sirve como material de información básica, y la mayoría de los ejercicios propuestos son fáciles de resolver de acuerdo con lo explicado en la conclusión. Cada ejemplar en su introducción detalla el uso de la simbología correspondiente, estructura del texto en unidades, secciones y contenidos, abarcando al final de cada sección un comprobemos lo aprendido, que es un resumen de ejercicios de los contenidos abordados para reafirmar los aprendizajes y en la mayoría de los casos como re alimentación para una evaluación sumativa, que pueden ser pruebas objetivas individuales y trabajos en pareja tomados de la prueba de unidad. (p. 7)
- Guía del docente: tiene como finalidad brindar una propuesta de programación anual, sugerencias sobre el uso del libro de texto de los estudiantes, mostrar la secuencia de los contenidos, indicar los aspectos esenciales, el uso correcto de la pizarra, ofrecer los solucionarios con sus procedimientos y fomentar la evaluación formativa con las pruebas de unidad. Además, implementa la enseñanza basada en el estudiante, rol del estudiante, del docente y retos de ambos participantes. Sin embargo, la guía proporciona información importante para facilitar el aprendizaje en los estudiantes y las pautas del plan de pizarra que el docente debe tomar en cuenta como lo expresa MINED (2019b):
- En caso de que el problema sea de enunciado extenso, se debe escribir un resumen comprensible de dicho enunciado.
- En el proceso de solución no debe repetirse cada palabra de la solución planteada en el Libro de Texto, pero sí debe escribirse cada paso imprescindible del proceso.
- La conclusión también puede mostrarse de forma resumida (cuando esta es extensa).
- Debe brindarse espacio suficiente para resolver al menos el primero de cada serie de ejercicios propuestos.
- Si no puede seguir escribiendo en la pizarra debido a su pequeño tamaño, puede borrar los contenidos que los estudiantes ya han terminado de copiar y escribir la continuación o bien dividir la pizarra en dos columnas con el mismo espacio en cada una. (p.13)
- La figura 2 muestra de manera resumida el actuar docente en cada punto del desarrollo de la clase, con un tiempo específico como lo indicó la figura 1. Es de vital importancia que el docente maneja dicha estructura, dado que es la secuencia para abarcar cada contenido y cumplir con el objetivo de la misma.
Figura 2: Estructura del plan de pizarra en la guía del docente 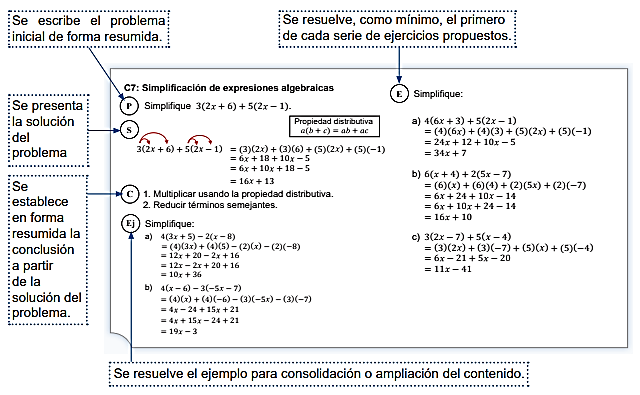
Fuente: Guía para docentes de educación secundaria a estudiantes de décimo grado. MINED (2019b, p.12)
- Cuaderno de actividades: es un material complementario al libro de texto del estudiante teniendo como finalidad consolidar los aprendizajes adquiridos en el aula, a través del trabajo independiente en casa diariamente. En cuanto a su estructura presenta inicialmente aspectos claves en cada sección, ejercicios básicos similares al abordado en la clase y al final problemas avanzados que generan un consolidado de mayor análisis y reflexión de los contenidos y, por si fuera poco, el solucionario de los mismos al final del libro. Al final se muestra el link2 del portal educativo Nicaragua educa para acceder a estos materiales didácticos.
La estructura del plan de pizarra según MINED (2019b, p.7) conlleva una serie de pasos a seguir por eso se considera metodología activa en la que se detallan los aspectos:
 Para plantear el problema inicial en la pizarra solo se escribe “P” seguidamente el enunciado del mismo o la orientación del ejercicio, en este punto el estudiante debe pensar en cómo resolverlo y el docente debe generar este espacio. Ningún estudiante pasa a la pizarra a resolverlo en este momento, solo lo resuelve en el cuaderno y puede explicar de forma oral como lo hizo, una vez que el maestro habiendo constatado esto procede a dar solución. También, puede darse el caso que más de algún alumno lo resuelva por lo que el docente parte de esto cuando recorre el aula y observa tal dificultad. En muchas ocasiones no se inicia con un problema inicial se parte con una definición, cuando es necesario partir de un concepto o introducir un nuevo contenido que los estudiantes no han visto. En los que se pueden escribir la palabra o una “D” de definición o demostración o se escribe concepto.
Para plantear el problema inicial en la pizarra solo se escribe “P” seguidamente el enunciado del mismo o la orientación del ejercicio, en este punto el estudiante debe pensar en cómo resolverlo y el docente debe generar este espacio. Ningún estudiante pasa a la pizarra a resolverlo en este momento, solo lo resuelve en el cuaderno y puede explicar de forma oral como lo hizo, una vez que el maestro habiendo constatado esto procede a dar solución. También, puede darse el caso que más de algún alumno lo resuelva por lo que el docente parte de esto cuando recorre el aula y observa tal dificultad. En muchas ocasiones no se inicia con un problema inicial se parte con una definición, cuando es necesario partir de un concepto o introducir un nuevo contenido que los estudiantes no han visto. En los que se pueden escribir la palabra o una “D” de definición o demostración o se escribe concepto.
 La solución, en este momento el docente explica el ejercicio con todas sus generalidades paso a paso, citando ejemplos del medio y sin descuidar la atención de sus educandos, resuelve con ellos el problema planteado, este no copia la solución de manera anticipada y puede contestar a las interrogantes planteadas.
La solución, en este momento el docente explica el ejercicio con todas sus generalidades paso a paso, citando ejemplos del medio y sin descuidar la atención de sus educandos, resuelve con ellos el problema planteado, este no copia la solución de manera anticipada y puede contestar a las interrogantes planteadas.
 En este punto, es la conclusión o el concepto de lo que se presentó en la solución reafirmando en un esquema o de manera resumida aspectos importantes del contenido, el docente hasta este punto pide a sus estudiantes usar el libro de texto según MINED (2019a), para copiar en su cuaderno y el educador puede copiar palabras claves en la pizarra o solo los pasos de solución como se presenta en MINED (2019b). Cabe mencionar que el docente puede hacer uso de algún material didáctico para llevar dicha conclusión y solo colocarla en la pizarra en los casos que los escolares no tuviesen los libros de texto a mano. Lo anterior depende de cada docente y se debe constatar que ellos tengan esto en su cuaderno.
En este punto, es la conclusión o el concepto de lo que se presentó en la solución reafirmando en un esquema o de manera resumida aspectos importantes del contenido, el docente hasta este punto pide a sus estudiantes usar el libro de texto según MINED (2019a), para copiar en su cuaderno y el educador puede copiar palabras claves en la pizarra o solo los pasos de solución como se presenta en MINED (2019b). Cabe mencionar que el docente puede hacer uso de algún material didáctico para llevar dicha conclusión y solo colocarla en la pizarra en los casos que los escolares no tuviesen los libros de texto a mano. Lo anterior depende de cada docente y se debe constatar que ellos tengan esto en su cuaderno.
 En el ejemplo se presentan variantes del problema inicial que son importantes señalar para poder reforzar lo aprendido. Algunos contenidos no tienen este momento, por lo que el docente en el planeamiento didáctico deber distribuir bien el tiempo para poder cumplir con el tiempo designado o enfatizar más en algunas condiciones del problema inicial.
En el ejemplo se presentan variantes del problema inicial que son importantes señalar para poder reforzar lo aprendido. Algunos contenidos no tienen este momento, por lo que el docente en el planeamiento didáctico deber distribuir bien el tiempo para poder cumplir con el tiempo designado o enfatizar más en algunas condiciones del problema inicial.
 Este es el momento de ejercitación, donde se presentan ejercicios para que los alumnos puedan resolverlo ellos mismos, se debe tomar muy en cuenta este tiempo en el planeamiento didáctico. No obstante, se copia únicamente el inciso “a” propuesto en el libro de texto y se les pide que lo resuelvan, el docente recorre el aula para constatar la solución en el cuaderno y posteriormente invitar a alguno a la pizarra de forma voluntaria, al terminar lo anterior, se prosigue con el inciso “b” realizando lo antes expuesto hasta agotar los ejercicios propuestos de ese contenido, Ahora bien, en la mayoría de los casos solo da el tiempo de resolver el inciso “a” y si la mayoría logró resolverlo se puede concluir que existió aprendizaje. En este tiempo puede revisar y firmar los cuadernos de los estudiantes que terminaron. También el docente puede intervenir para aclarar dudas en el caso que algún estudiante resolvió de manera incorrecta el ejercicio y se reafirma nuevamente. El realizar lo anterior y pasar al estudiante a la pizarra se verifica que el estudiante si aprendió, por que logró resolver el ejercicio, verificándose también, al aplicarse la prueba objetiva.
Este es el momento de ejercitación, donde se presentan ejercicios para que los alumnos puedan resolverlo ellos mismos, se debe tomar muy en cuenta este tiempo en el planeamiento didáctico. No obstante, se copia únicamente el inciso “a” propuesto en el libro de texto y se les pide que lo resuelvan, el docente recorre el aula para constatar la solución en el cuaderno y posteriormente invitar a alguno a la pizarra de forma voluntaria, al terminar lo anterior, se prosigue con el inciso “b” realizando lo antes expuesto hasta agotar los ejercicios propuestos de ese contenido, Ahora bien, en la mayoría de los casos solo da el tiempo de resolver el inciso “a” y si la mayoría logró resolverlo se puede concluir que existió aprendizaje. En este tiempo puede revisar y firmar los cuadernos de los estudiantes que terminaron. También el docente puede intervenir para aclarar dudas en el caso que algún estudiante resolvió de manera incorrecta el ejercicio y se reafirma nuevamente. El realizar lo anterior y pasar al estudiante a la pizarra se verifica que el estudiante si aprendió, por que logró resolver el ejercicio, verificándose también, al aplicarse la prueba objetiva.
 Momento de las tareas en casa, estas se orientan muchas veces de forma oral a los estudiantes, señalando el número de ejercicio, número de página en el cuaderno de actividades y el número de página del libro de texto como parte del trabajo independiente en casa. A continuación, un ejemplo de la anterior (C/A, Ejercicio 64, pág.16 L/T, pág.78). Algunas veces se escriben en la pizarra y es revisado por el docente en el momento que considere pertinente.
Momento de las tareas en casa, estas se orientan muchas veces de forma oral a los estudiantes, señalando el número de ejercicio, número de página en el cuaderno de actividades y el número de página del libro de texto como parte del trabajo independiente en casa. A continuación, un ejemplo de la anterior (C/A, Ejercicio 64, pág.16 L/T, pág.78). Algunas veces se escriben en la pizarra y es revisado por el docente en el momento que considere pertinente.
Con base a lo anterior, el aprendizaje de matemáticas logra ser significativo y activo porque el estudiante en el desarrollo de la clase pone en práctica lo que aprendió, por eso se sugiere que el docente no borre la pizarra en lo que respecta al problema inicial, solución, conclusión y ejemplo para que el estudiante al resolver pueda observar los procedimientos realizados e intente dar solución a los ejercicios en la ejercitación.
Continuamente a este proceso es activo porque en todo el tiempo de la clase el estudiante pone en práctica sus habilidades y conocimientos, es decir, indica ponerlo a pensar y es amigable por que los contenidos van del más sencillo al complejo enseñando cada aspecto de una unidad por temas separados. Por ejemplo, lo que se muestra en la siguiente figura:
Figura 3 Unidades y secciones del libro de texto de matemáticas de Décimo grado
Fuente: Libro de texto de décimo grado (MINED, 2019c, p. 6)
En décimo grado se inicia con la unidad de Conjuntos e intervalos numéricos esta tiene dos secciones. La sección 1 tiene 5 contenidos y la sección 2 tiene 3 contenidos, si se analiza la jerarquía de los contenidos en cada una de las secciones para la Sección 1: C1: Conjunto, elemento, notación por extensión, pertenencia y cardinalidad de conjunto; C2: Diagrama de Venn, operaciones con conjuntos (Unión e intersección), conjunto vacío; C3: Conjunto universal. Relaciones entre conjuntos (Inclusión e igualdad); C4: Operaciones con conjuntos (Diferencia y complemento); C5: Conjunto (notación por comprensión); Para la Sección 2: C1: Intervalos numéricos en la recta numérica; C2: Unión de intervalos numéricos; C3: Intersección de intervalos numéricos. Lo anterior fue tomado del libro de texto para estudiantes de 10mo grado.
Si se observa la sección 1 aporta en sus 5 contenidos los conocimientos necesarios para poder aplicar los conceptos de unión e intersección en la sección 2 sobre intervalos numéricos, donde el estudiante va aprendiendo de forma sucesiva cada concepto y su aplicación de cómo interpretarlo, esto resulta amigable por no se le proporciona todos estos contenidos a los estudiantes en uno o dos periodos de clases de 90 minutos como se hacía antes de la implementación de esta metodología, por lo que el estudiante diariamente va recibiendo un contenido hasta llegar al punto clave donde se aplican todos los aprendizajes y al estudiante le resulta cómodo y entretenido ir aprendiendo matemáticas de una forma más gradual y no tan compleja.
Al observarse la relación de la unidad 1 con la unidad 2 la primera sirve para asimilar todos los conceptos primordiales para la resolución de inecuaciones en cuanto su resolución, gráfica y el conjunto solución. Por esta razón, las matemáticas con esta metodología resultan, fáciles de comprender, jerárquicas al aumentar la complejidad, asimilación de contenidos y amigables por la manera de presentarse al estudiante, además que no proponen ejercicios complejos, también depende de la didáctica y pedagogía que el docente tenga para transmitir esos conocimientos, además que se puede poner en práctica el aprendizaje por andamiaje3 y zona del desarrollo próximo4 al ponerlos a trabajar en pareja, para en los casos que el estudiante no entienda el contenido su compañero de clase pueda ser el que ayude a entender el contenido. Añadiendo que el comprobemos lo aprendido ayuda a refirmar todos los contenidos de la sección y ese día es de práctica en el aula y el docente puede reunirlos en pareja para resolver los ejercicios propuestos y aclarar las dudas.
Sin embargo, los instrumentos de evaluación sugeridos son las pruebas de unidad, estas se aplican terminando cada una para valorar si el estudiante logra aplicar lo que aprendió, pero es complicado muchas veces cuando una de ellas tiene varias secciones y esta tiene muchos contenidos, podría pasar que el estudiante no logre resolver toda la prueba, por los distintos estilos de aprendizaje como y es tarea del docente lograr identificar en cada sesión de clase el porcentaje de asimilación de sus estudiantes.
En cuanto al uso de las tecnologías de la información y la comunicación (TIC), en muchas ocasiones este uso se limita o no ocurre por la metodología del plan y puesto que algunos contenidos no tienen ese carácter por la abstracción y otro factor es el tiempo de 45 minutos donde se debe adecuar cada momento para poder hacer uso de la tecnología y aplicaciones. Por el contrario, según Herrera Castrillo (2021):
Las tecnologías de la información y la comunicación (TIC) juegan un papel muy importante, para el desarrollo de las asignaturas, permite a los estudiantes comprender, analizar e interpretar de forma científica y práctica los contenidos y alcanzar los objetivos propuestos desde inicio del curso. (p.16)
A lo que el docente como parte de sus estrategias innovadoras podría incorporar dicho uso en uno o dos de sus momentos, dado que existen un sin número de aplicaciones para matemáticas como: Geogebra, Hiper Scientific calculator, simulador PhET, Quiziz, mimind, entre otras, que sirven para el aprendizaje y evaluación.
Dentro de la metodología del plan de pizarra en matemáticas los resultados que evidencian que el proceso de aprendizaje es significativo y amigable es el rendimiento académico dentro de la evaluación sumativa, que es el resumen de todas las evaluaciones en un periodo evaluativo. Se conoce que el programa sugiere aplicar las pruebas de unidad como instrumento de evaluación de los aprendizajes, pero también sugiere trabajos escritos, entrega de tareas, el trabajo en el aula, cuestiones formativas como participación, atención en la clase, conducta. El programa da pautas para asignar menos puntaje a las pruebas de unidad, puesto sugiere asignar 20 puntos como máximo y que no se pueden aplicar evaluaciones mayores a este puntaje en cada corte evaluativo5.
Cabe mencionar que, el hecho de realizar una prueba, esta debe tener a la par su instrumento de evaluación para medir los distintos aspectos, que demuestren por qué el estudiante obtuvo cierta calificación y de esa misma manera, dar una realimentación a los estudiantes respecto a lo que tuvieron dificultades en algunos ítems.
Para demostrar que los objetivos del plan pizarra contribuyen a mejorar el aprendizaje de los estudiantes, los resultados en las pruebas de unidad deben ponerse en evidencia y que, por ende, el rendimiento académico será satisfactorio, puesto es la finalidad del programa, aumentar el índice de aprobación y cambiar las concepciones negativas que se tienen hacia la asignatura de Matemáticas.
MATERIALES Y MÉTODOS
Para la obtención de los datos necesarios y demostrar que los aprendizajes en la asignatura de Matemáticas, son significativos y amigables a través de la metodología del plan de pizarra, al usar el método empírico, se aplicó las pruebas de unidad en dos fases a estudiantes de décimo grado del Instituto Nacional Eddy Alonso en la ciudad de Sébaco, departamento de Matagalpa en el segundo semestre del año escolar 2022 en los cortes evaluativos III y IV.
La población de estudiantes de los décimos grados de las secciones del A al F fue de 176 estudiantes, por lo que se aplicó un muestreo probabilístico como lo expresan los autores Hernández Sampieri, Fernández Collado y Baptista Lucio (2014) que:
Todos los elementos de la población tienen la misma posibilidad de ser escogidos para la muestra y se obtienen definiendo las características de la población y el tamaño de la muestra, y por medio de una selección aleatoria o mecánica de las unidades de muestreo/análisis. (p.208)
De acuerdo con los autores y relacionando con este estudio, se conoció una población finita de estudiantes y de ahí se extrajo una muestra para la aplicación de la prueba objetiva. Se usó la ecuación estadística, cuando se conoce el tamaño de la población a un nivel de confianza del 95 %, con una probabilidad de éxito del 0,90 y de fracaso del 0,10 y un error máximo admisible del 5% al aplicar la ecuación
Donde N son los 176 estudiantes; es el nivel de confianza al 95% correspondiente al valor Z de 1,96; p es la probabilidad de éxito y q la probabilidad de fracaso y d error máximo admisible de 0,05, al realizar dicho cálculo se obtuvo una muestra aproximada de 78 estudiantes correspondiente al 44,3 % de la población. Tal como se demuestra el cálculo:
Como fueron varias secciones la muestra de los estudiantes, se realizó un cálculo proporcional según la cantidad de estudiantes cada una de las secciones, luego se multiplicó por el 44,3% cada cantidad, resultando lo que muestra la tabla 1, y posteriormente las pruebas se aplicaron de forma aleatoria en cada sección. Como un ejemplo del cálculo anterior seria lo siguiente: Para la sección A, donde existieron n1 = 26 estudiantes y nA seria la muestra calculada.
nA = (%muestra) (n1) = (0,443) (26) ≈ 12 estudiantes
De la misma manera, se realizó el cálculo de la muestra para las demás secciones.
Tabla 1: Resultados del cálculo de muestra por sección.
| Sección | Población | Muestra |
| A | 26 | 12 |
| B | 32 | 14 |
| C | 28 | 12 |
| D | 29 | 13 |
| E | 34 | 15 |
| F | 27 | 12 |
| Total | 176 | 78 |
Fuente: Elaborado por el autor
En la tabla anterior se observa el cálculo de muestra para cada sección, la selección de estudiantes se realizó al azar, para evitar la conveniencia de los resultados y así obtener resultados verdaderos.
Fases de aplicación de las pruebas o etapas de la investigación
Las pruebas se aplicaron en dos fases. En la primera fase se utilizó la prueba de unidad al terminar la unidad 5: Introducción a la trigonometría que tiene 4 secciones y cada una tiene 4 y 5 contenidos respectivamente.
Para la segunda fase se empleó la prueba de unidad, pero seccionada, es decir, cada vez que terminaba una sección se aplicaba parte de los ítems de la prueba de unidad de cada sección. Eso con el fin de realizar un contraste de los resultados de las pruebas que propone el MINED y analizar los rendimientos de los resultados en cada caso, valorando los más significativos en cuanto a ejercicios resueltos correctamente y no a puntaje, siendo así meramente formativo para realizar una predicción de los resultados sumativos.
Para el procesamiento de la información, se agrupó en tablas de frecuencias en Microsoft Excel y se usó el programa estadístico SPSS para el análisis y creación de gráficos. Luego de aplicar las pruebas, se ejecutó en el software ya mencionado para ayudar a generar la solución.
RESULTADOS Y DISCUSIÓN
Dentro del análisis para la primera fase se realizó por ítems, la prueba de unidad para la unidad 5 contiene 4 ítems y cada ítem 3 incisos referente a funciones trigonométricas seno, coseno y tangente. Para la fase 2 de la prueba de unidad respecto a la unidad 6 contiene 4 ítems con varios incisos, esta prueba se dividió en 4 partes una por sección dado que, esta unidad contiene 4 secciones; se tomaron dos incisos de la prueba y uno del cuaderno de actividades. El docente impartió las clases correspondientes con sus respectivos “comprobemos lo aprendido”. Cuando se terminó la unidad 5 se realizó la prueba un día después de haber hecho el repaso general.
Seguidamente se efectuó lo mismo con la unidad 6 aplicando la prueba por secciones, mencionando que para la segunda fase se le aplicó la prueba a los mismos estudiantes que realizaron la prueba de la unidad 5, para no tener discrepancias respecto al aprendizaje de los estudiantes, con finalidad de diferenciar los resultados de aplicar las pruebas de unidad según sugiere el programa y aplicar la prueba de forma seccionada, puesto la unidad 5 demoro casi 2 meses en terminar.
Siguiendo con el procesamiento de la información, el docente realizaba otras evaluaciones a la par para no descuidar el proceso normal y que los puntajes obtenidos con el estudio se incluyeran en las calificaciones de los estudiantes. Las pruebas se encuentran al final del articulo como anexo.
Para que se realizara un buen análisis la prueba de la fase 2, se estudió según la prueba 1 por ítems 1, 2, 3 y 4, como la prueba 2 se seccionó y se hizo 4 pruebas cortas las cuales se marcaron como ítems 1,2,3 y 4 para realizar el contraste. Al corregir las pruebas y obtener los resultados se colocaron escalas como B: Bueno, R: Regular y FR: Falta reafirmar.
Siguiendo con lo anterior, se usó el método empírico para organizar los datos, se procedió a usar el estadístico para procesar dichos resultados, a lo que se obtuvo al aplicar la prueba de unidad (ver en anexo 1) al terminar la unidad 5: Introducción a la trigonometría.
El gráfico No.1 muestra que la mayoría de los estudiantes respondieron de manera regular a los ítems de la prueba, a lo que se evidencia que ellos necesitan reforzar sus conocimientos son más que aquellos que hicieron correctamente los ejercicios, esto puede ser ocasionado debido a que los alumnos no recordaron las primeras secciones de la unidad resolviendo de forma incorrecta, esto ocurrió con los reactivos problema de las 3 primeras secciones, mejorando un poco en los ítems de la última sección, puesto es entendible que recién concluyen de ver esos contenidos.
Gráfico 1: Resultados de la aplicación de la prueba de la unidad 1
Universo de estudio: 78 estudiantes
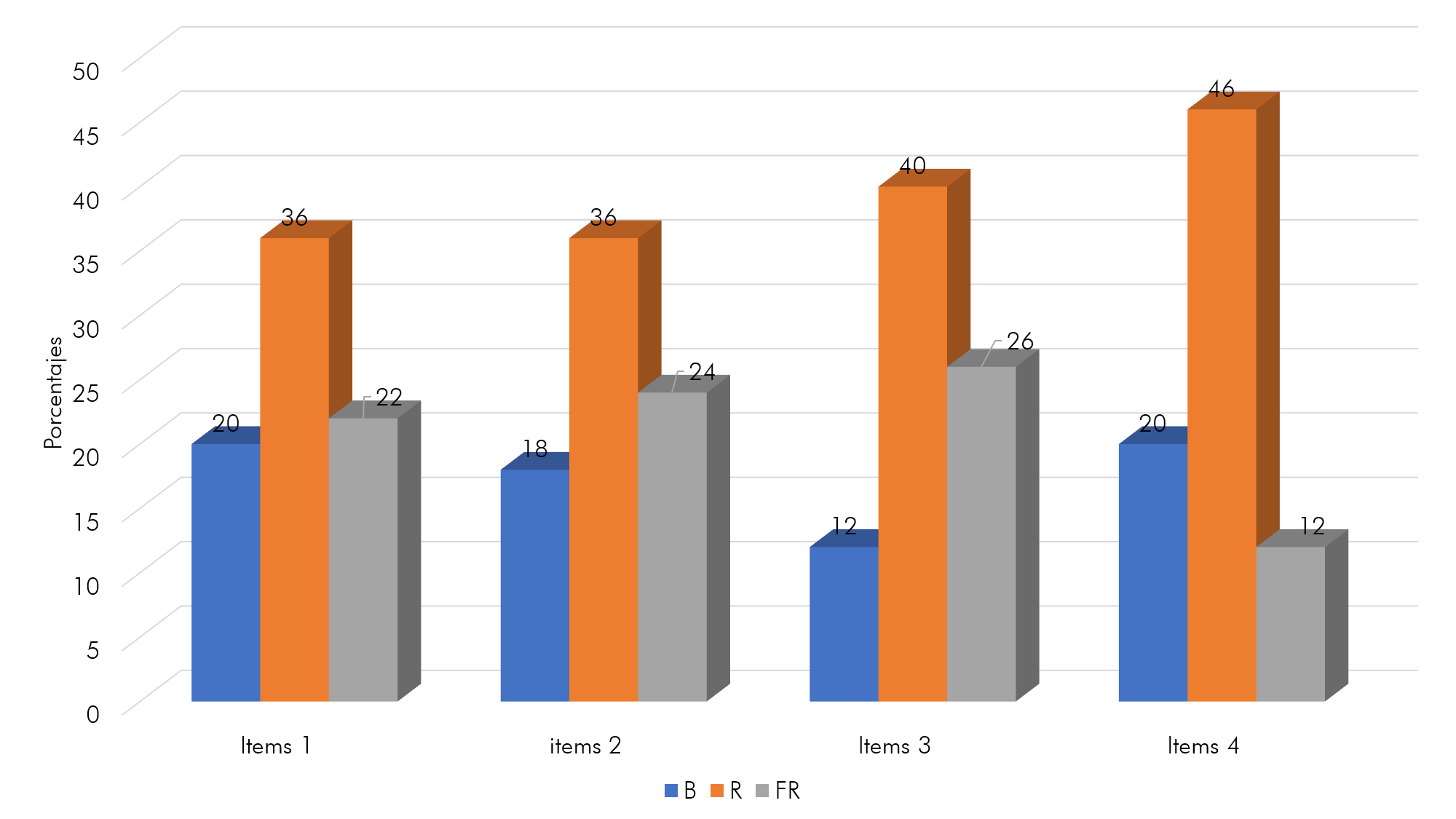
Fuente: Datos obtenidos al aplicar la prueba de unidad al terminar la unidad 5.
Por añadidura, es desventajoso aplicar una prueba al terminar una unidad completa puesto pasan muchos días y los estudiantes van recibiendo los contenidos diariamente, y se les dio el debido repaso, al llegar comprobemos lo aprendido que se encuentra cuando se termina una sección, pero si se trata de que el plan pizarra va avanzando paulatinamente los contenidos y subiendo la complejidad para cada uno solo un 26% de ellos, logra establecer el vínculo deseado, además que el proceso es continuo y puede pasar que el estudiante logre confundir o no diferenciar lo que va a resolver en cada ítem.
Aparte de que, el estudiante, según la metodología del programa, cada ítem se debe resolver sin calculadora y debe memorizar o manejar los valores de las funciones trigonométricas para los ángulos de 30º, 45º, 60º y 90º, lo que resultó algo complicado para ellos. Se observa que se debe mejorar la forma de evaluación para cumplir con el objetivo del rendimiento académico en matemáticas.
Por consiguiente, los resultados de los puntos obtenidos se encontraron en una escala entre aprendizaje elemental (AE) y algunos en las escalas superiores como satisfactorio (AS) y avanzado (AA). Cabe señalar, que la prueba la realizaron en un tiempo de 45 minutos, que es el tiempo que dura la clase normal. Por ende, las demás evaluaciones fueron revisión de tareas, las participaciones de cada estudiante, algunos trabajos en pareja, asistencia y puntualidad aunque este parámetro no fue muy tomado en cuenta por la incidencia de la pandemia de la COVID -19 donde existió que muchos estudiantes se enfermaron ellos o sus familiares, teniendo el cuidado de aplicar la prueba a los que asistieron de manera regular al instituto, por lo que si quedaba alguno de este tipo de caso, no se tomaba en cuenta y se le asignaba otro, esto ocurrió solo en 3 casos en distintas secciones.
El gráfico No. 2 muestra los resultados obtenidos al aplicar la prueba de unidad de la unidad 6: Funciones trigonométricas sugeridas por MINED, pero por sección, esto quiere decir que, cuando se terminaron los contenidos de una sección, se abordó el comprobemos lo aprendido y posteriormente se aplicaba la prueba con los ítems correspondientes a la sección. Por lo que se aplicaron 4 pruebas cortas al terminar las 4 secciones de la unidad, esta es una metodología diferente a la que sugiere el MINED en su manual y en las guías para el docente. Cada prueba se tomó como un solo ítems para cada prueba contenida 3 incisos únicamente (Ver anexo 3)
Gráfico 2: Resultados de la aplicación de la prueba de la unidad 6
Universo de estudio: 76 estudiantes
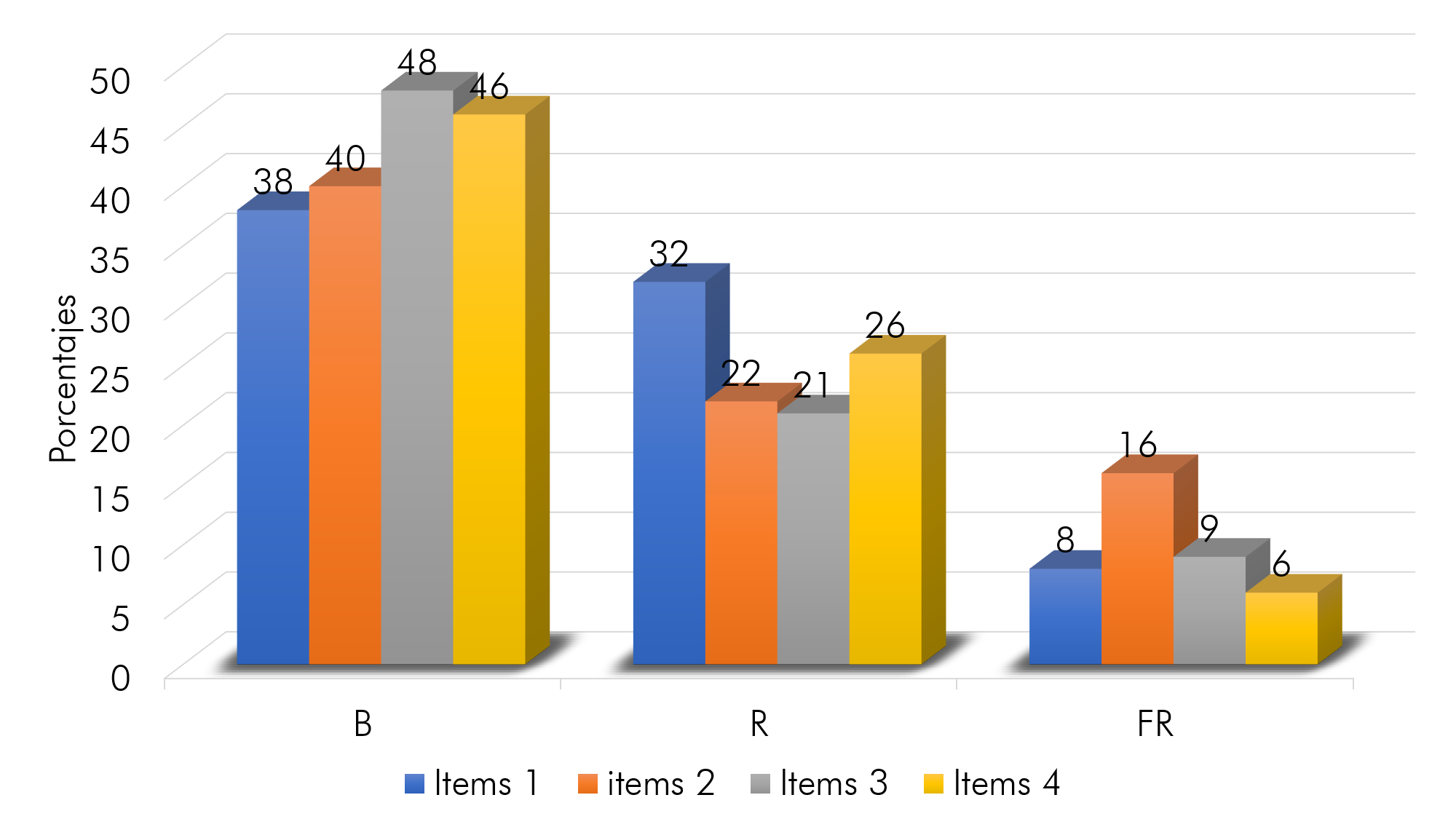
Fuente: Datos obtenidos por el autor al aplicar la prueba de unidad al terminar cada sección de la unidad 6.
Para generar el gráfico anterior, las pruebas del anexo 3 se fueron aplicando al terminar cada sección, se corrigieron y los datos iban siendo acumulados en una tabla, hasta que se aplicó la última prueba, luego se procedió a analizar los resultados. Es evidente que los resultados son satisfactorios, la mayoría de los estudiantes obtuvo la escala de Bueno en la mayoría de los ítems y regular, esto por lo que la manera que se aplicó o dividió esta vez fue distinta y el estudiante fue poniendo en práctica los conocimientos aprendidos continuamente añadiendo que, se les permitió hacer uso de la calculadora científica y se les enseñó como operarla. Contrariamente, al plan de pizarra que orienta al estudiante a usar una tabla de valores para las funciones trigonométricas para valores en grados de 0 a 90.
Conjuntamente los resultados proporcionados fueron a la par con los reforzamientos cuando se les brindo su calificación, se retomaba las dificultades encontradas. Está claro que es conveniente aplicar las pruebas terminando una sección, dado que presenta al docente la información requerida para tomar decisiones para mejorar los aprendizajes aplicando estrategias que se puedan adecuar a la metodología planteada.
Si se pretende mejorar el rendimiento académico, la aplicación de las pruebas de unidad genera mejores resultados aplicarlas de forma seccionada, de modo que se conoce que el docente realiza otras evaluaciones, además que involucra un poco más de trabajo para el docente, pero es una manera más eficaz de aprovechar lo aprendido por el estudiante y que lo aplique sin obviar los estilos de aprendizaje de cada uno, que esto ocurrió en periodo de pandemia de la COVID-19, donde las preocupaciones de contagio por los estudiantes y padres de familia fue latente.
Sin embargo, no se puede omitir que, si el estudiante muestra interés a la clase, existe motivación y cumple con sus tareas diariamente el proceso se vuelve integrado y provechoso. Añadiendo que, este tipo de metodología es congruente a lo que se realizó con la evaluación, a lo que el programa hace en ir avanzando con los contenidos programados de forma gradual, lo ideal fuese hacer lo mismo con la evaluación, ahora bien, se maneja que es evaluación formativa en el desarrollo de cada sesión de clase, pero es necesario medir al estudiante su avance en asimilación de contenidos. Es lógico que, si los estudiantes demuestran buenos resultados en estas pruebas, significa un vector de que el rendimiento académico final en el corte evaluativo será muy bueno.
Se analizó únicamente las pruebas de unidad, pues son un resumen de forma general de cada unidad, puede ser que MINED las oriente como una perspectiva de los avances en matemáticas, pero es una metodología activa, por la permanencia de la evaluación formativa, amigable, por el nivel de complejidad de los temas que se abordan, de los ejercicios propuestos y de la cantidad de ejercicios a resolver. Congruente a la anterior, el recibir la clase diariamente no se pierde el hilo conductor de los contenidos y se lleva la secuencia en cada sesión de clase, tomando el anterior para entender el que prosigue.
El plan de pizarra además de jerarquizar los contenidos de una forma más sencilla, accesible para el estudiante, vino a romper los esquemas de que las matemáticas son difíciles, y de esa manera cambiar la apatía que la mayoría de los estudiantes tiene hacia la asignatura y a fomentar que el mismo aprenda lo básico, necesario y se enamore de la asignatura, pero esto depende de cada docente.
Para el docente el plan de pizarra comenzó a cambiar su forma de organizar su clase en su planeamiento, desarrollo de la clase al usar el pizarrón y no es que los planes de clases ya estén elaborados, están los planes didácticos ya propuestos, pero es trabajo del docente dar el toque personal, de cómo abordar cada aspecto, repartir el tiempo para cada momento, velar por la concentración de sus alumnos al momento de la clase e ir resolviendo las asignaciones con ellos y no solo es copiar todo el plan pizarra de un solo y luego explicarlo, sino ir desarrollando cada momento según se corresponde. Al mismo tiempo estar atento que los estudiantes resuelvan los ejercicios propuestos y hacer uso de los materiales didácticos.
CONCLUSIONES
- La metodología del plan de pizarra, genera un aprendizaje activo, por que hace que el estudiante piense en cómo resolver el problema inicial o un ejercicio, basándose en sus conocimientos previos o en los contenidos anteriores que se le fueron dados, además de que en el desarrollo de la clase se insta al educando, a ser participativo, a ser capaz de expresar de forma oral sus ideas e inquietudes y resolver los ejercicios en su mayoría muy acertados a la respuesta correcta.
- El impacto de implementar dicha metodología y evaluación genera un aprendizaje significativo, porque los estudiantes logran aplicar lo aprendido a los ejercicios y recuerdan esto en los próximos contenidos, generando los cambios conceptuales necesarios para que el aprendizaje pueda aplicarlo a otras situaciones.
- También, es amigable por el nivel de complejidad de los ejercicios que se le proponen al estudiante, la cantidad de ejercicios a resolver durante la clase y en las tareas en casa, la forma gradual del cómo se van desarrollando los contenidos diariamente, partiendo de los básicos, elementales y sencillos hasta un nivel algo complejo, es decir, que pueda aplicar fácilmente lo que aprendió.
- La evaluación de los aprendizajes en la mayoría de las sesiones de clase que fueron objeto de investigación, fue formativa, valorando únicamente los aciertos y desaciertos del estudiante y fue sumativa al final de la unidad, pero resultó más adecuado aplicar las pruebas de unidad por cada sección de contenidos, con mucha desventaja al aplicar la prueba de unidad para toda la unidad completa, esto si se habla de dar resultados para los cortes evaluativos, dado que al estudiante se le dificulta poder recordar muchos contenidos y algoritmos.
- El plan de pizarra es parte del planeamiento didáctico del docente y funciona también como metodología para guiar el aprendizaje del estudiante de una manera más organizada, esquemática, sencilla y enfocada siempre a que el mismo se enamore de las matemáticas.
Es de vital importancia para los investigadores que pretendan realizar estudios en esta línea, y con base a la experiencia del autor en el aula de clase, se recomienda ampliar sobre:
- El uso y forma de adecuar las TIC a la metodología del plan de pizarra en educación secundaria.
- El impacto de los aprendizajes obtenidos con el plan de pizarra en la educación superior.
- Nivel de relación de la metodología del plan de pizarra en secundaria con los modelos universitarios específicamente para las asignaturas que contengan matemáticas.
- Análisis de la forma de evaluación de los aprendizajes del plan de pizarra desde una perspectiva con enfoque constructivista o didáctico y por competencias.
- La interdisciplinariedad que se puede lograr con la metodología del plan de pizarra con otras asignaturas.
- Estrategias didácticas pertinentes que se pueden adecuar a los momentos del plan de pizarra para mejorar el aprendizaje.
- El nivel de pertinencia del uso de los recursos didácticos del plan de pizarra entre ellos libros de textos, guía del docente y cuaderno de actividades.
Finalmente, de manera atenta y afectiva se agradece a los estudiantes de décimo grado del año escolar 2022 que participaron al resolver las pruebas en las dos fases, cuando se les hizo la convocatoria. A los colegas cercanos al autor que ayudaron a generar ideas para seguir con la investigación y realizar revisiones generales.
REFERENCIAS BIBLIOGRAFICAS
Hernández Sampieri, R., Fernández Collado, C., & Baptista Lucio, M. (2014). Metodología de la investigación. México, DF: McGRAW-HILL.
Herrera Castrillo, C. J. (2021). Aprendizaje en las asignaturas “Electricidad” y “Termodinámica y Física Estadística” en tiempos de pandemia. Revista Multi-Ensayos, 7(13), 14-25. Obtenido de https://doi.org/10.5377/multiensayos.v7i13.10748
Huber, G. L. (2008). Aprendizaje activo y metodología educativa. Active learning and methods of tecahing. Tiempos de cambios universitarios, 59.
MINED. (2019a). Manual interactivo sobre el plan de pizarra, proyecto para el aprendizaje amigable de Matemática en educación secundaria (Primera ed.). Managua, Nicaragua: MINED, JICA.
MINED. (2019b). Guía para docentes de Matemáticas educación secundaria de 7mo a 11mo grado (Primera ed.). Managua, Nicaragua: MINED, JICA.
MINED. (2019c). Libro de texto de Matemáticas para estudiantes de 10mo grado educación secundaria. Managua, Nicaragua: MINED, JICA.
ANEXOS
Anexo 1- Ejemplo del plan didáctico del contenido 1 de la unidad 5
Anexo 1- Ejemplo del plan didáctico del contenido 1 de la unidad 5
PLAN DE CLASES
Nombre del Centro: Instituto Nacional Eddy Alonso Docente: Disciplina: Matemáticas
Grado: Décimo Sección: A, B, C, D, E, F Tiempo: 45 min Fecha:
Competencia de Grado: #5.1 Resuelve situaciones en diferentes contextos, relacionadas con las funciones trigonométricas para ángulos agudos.
Competencia de eje Transversal: # 5.1 Identidad Personal, Social y Emocional: Fortalece su autoestima, confianza y seguridad, al respetarse a sí mismo y a las demás personas reconociendo sus características, necesidades, roles personales y sociales. Indicador de logro: #5.1 Resuelve situaciones en diferentes contextos, relacionadas con las funciones trigonométricas de ángulos agudos en triángulos rectángulos, que le ayuden a fortalecer su autoestima. Aprendizaje Esperado: Aplica el Teorema de Pitágoras para encontrar la longitud desconocida de un lado de un triángulo.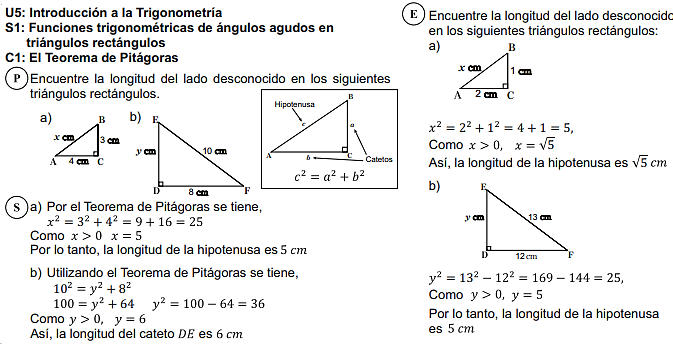
C/A, Ejercicio 64, pág.16 (L/T, pág.78)
ANEXO 2: Prueba de unidad correspondiente a la unidad 5



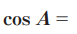
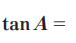


ANEXO 3: Pruebas de unidad 1, 2, 3 y 4 correspondiente a la unidad 6 seccionada
Cada una de las pruebas fueron tomadas de la prueba unidad y se seccionó en 4 partes para cumplir la propuesta y el análisis y se presentaron así en ese apartado por cuestión de reducir espacio, pero a los estudiantes se les presentó con los debidos espacios la igual que la prueba anterior.
Prueba 1



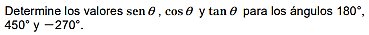
Prueba 2

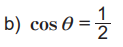
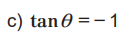
Prueba 3
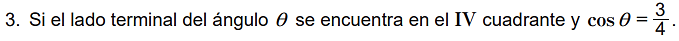
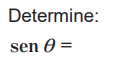
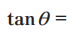
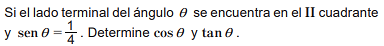
Prueba 4:
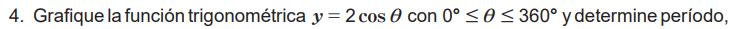
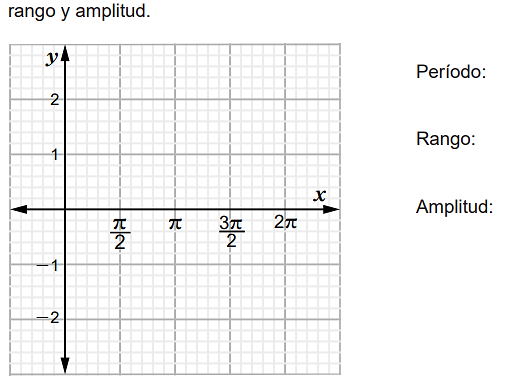
2 Portal educativo Nicaragua educa. Material didáctico para plan de pizarra. https://www.mined.gob.ni/biblioteca/page/10?category=librosdigitales&sc&post_type=product
3 Se refiere a aquellas estructuras, actividades o estrategias de apoyo que el docente realiza para que el alumno construya su propio conocimiento, basándose en el aprendizaje por la zona del desarrollo próximo.
4 Fue introducido por Lev Vygotski desde 1931, refiriéndose a la distancia existente entre el nivel de desarrollo efectivo del alumno y el nivel de desarrollo potencial delimitando a la incidencia la acción educativa.
5 Resultado de la evaluación final cuantitativo de 0 -100 puntos en un periodo de dos meses, en el año se realizan cuatro cortes evaluativos estos se promedian y da como resultado la nota final.
© 2023 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
