Área y Volúmenes de los Sólidos Platónicos
Area and Volumes of Platonic Solids
Arnoldo Abraham Herrera Herrera
Estudiante de Doctorado en Matemática Aplicada, Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0000-0003-3001-8861
arnoldo.herrera@unan.edu.ni
Ingrid Judith Orozco Martínez
Estudiante de Doctorado en Matemática Aplicada, Facultad Regional Multidisciplinaria de Matagalpa, UNAN-Managua/FAREM-Matagalpa, Nicaragua
https://orcid.org/0000-0002-1362-3579
judithorozco655@gmail.com
Iván Augusto Cisneros Díaz
Doctor en Matemática Aplicada. Universidad Nacional Autónoma de Nicaragua, Managua. UNAN-Managua, Nicaragua
https://orcid.org/0000-0003-2014-1946
ivan.cisneros@unan.edu.ni
Recibido
30/01/2023
Aceptado
21/03/2023
RESUMEN
Los sólidos platónicos son cinco cuerpos geométricos que comparten un conjunto de características geométricas similares. También reciben el nombre de sólidos perfectos, poliedros platónicos y de cuerpos cósmicos entre otras denominaciones. Los sólidos platónicos son poliedros regulares y convexos dentro de ellos están: tetraedro, cubo (o hexaedro), octaedro, dodecaedro e icosaedro. Este trabajo presenta las deducciones matemáticas de las fórmulas de áreas y volúmenes de los sólidos platónicos. El objetivo central es demostrar el análisis geométrico para obtener las fórmulas de áreas y volúmenes, a su vez reconocer que el estudio de las diferentes técnicas y métodos de demostración permiten aplicar el cálculo de áreas y volumen a la resolución de problemas prácticos que se presentan en diversas situaciones demostrativas de la matemática. Cabe destacar que estas formas de demostraciones están basadas en las propiedades básicas comunes de los objetos geométricos clásicos de la geometría. Por otra parte, el concepto de área y de volumen se generaliza a diversas figuras cerradas permitiendo así una mayor generalidad sobre dichos conceptos para construirse mediante otras estrategias de enseñanzas y aprendizaje. Finalmente, se realiza la programación de dichas fórmulas de áreas y volúmenes en el lenguaje de programación de alto nivel Python, utilizando el paradigma de programación funcional.
PALABRAS CLAVES
Área; volumen; sólidos platónicos; demostración.
ABSTRACT
Platonic solids are five geometric bodies that share a set of similar geometric characteristics. They are also called perfect solids, Platonic polyhedra and cosmic bodies among other names. Platonic solids are regular and convex polyhedra and include: tetrahedron, cube (or hexahedron), octahedron, dodecahedron and icosahedron. This paper presents the mathematical deductions of the formulas for areas and volumes of Platonic solids. The main objective is to demonstrate the geometric analysis to obtain the formulas of areas and volumes, while recognizing that the study of the different techniques and methods of demonstration allow the application of the calculation of areas and volume to the resolution of practical problems that arise in various demonstrative situations of mathematics. It should be noted that these forms of demonstrations are based on the common basic properties of the classical geometric objects of geometry. On the other hand, the concept of area and volume is generalized to several closed figures, thus allowing a greater generality on these concepts to be built through other teaching and learning strategies. Finally, the area and volume formulas are programmed in the high-level programming language Python, using the functional programming paradigm.
KEYWORDS
Area; volume; platonic solids; demonstration.
INTRODUCCIÓN
Uno de los principales problemas estudiado dentro del desarrollo metodológico de la matemática, es la construcción de las demostraciones matemáticas (Orozco, 2022). Los teoremas desarrollados en este artículo están referidos a la aplicación del cálculo de área y volumen de solidos platónicos, constituyen teoremas clásicos del área geométrica, por tanto, uno de los objetivos teóricos es presentar sus demostraciones a partir de algunas construcciones geométricas de polígonos conocidos, de manera que permitan obtener nuevos resultados poliédricos.
Las demostraciones presentadas ponen de manifiesto la importancia teórica y práctica del desarrollo de la matemática, específicamente en las demostraciones geométricas, permitiendo evidenciar el desarrollo del pensamiento geométrico y sobre todo establecer relaciones analíticas entre los diferentes objetos geométricos.
El estudio de los contenidos geométricos de los sólidos platónico constituye una posibilidad general matemática de generalizar fórmulas de áreas mediante las obtenidas en el estudio del cálculo de áreas para polígonos regulares, esto hace posible poder extender este conocimiento de manera más natural al aprendizaje propio del estudiante.
Como consecuencia de esta problemática, se plantean los principales valores metodológicos de este artículo:
- Formulación de estrategias demostrativas matemáticas, mediante la interrelación de polígonos regulares y propiedades de los sólidos platónicos.
- Aplicación de diferentes procesos constructivos basados en el cálculo de área y volumen de polígonos regulares y sus diversas de demostraciones matemáticas.
- Evidenciar la importancia de la búsqueda de nuevos enfoques de paradigmas demostrativos en Matemática.
- Implementación del código fuente de los diversos algoritmos en el lenguaje de Programación de alto nivel Python.
MATERIALES Y MÉTODOS
En este apartado se presenta el desarrollo de las diferentes demostraciones de las fórmulas de áreas y volúmenes de los cincos solidos plantónicos mediante la construcción básica de polígonos regulares y la aplicación de sus principales propiedades geométricas. Se muestra la dependencia que existe entre estos polígonos y sus principales características teóricas.
Todo esto permite obtener diferentes demostraciones geométricas, mediante la conjugación de diversas propiedades geométricas y poder obtener las diversas fórmulas de áreas y volumen de dichos solidos platónicos. En un sentido genérico, la metodología empleada es la obtención de diversas fórmulas de áreas y volumen, mediante diversa combinación de técnicas de construcciones geométricas, entre las cuales se pueden mencionar la perpendicularidad, el paralelismo, operaciones con rectas o segmentos y operaciones con ángulos Gámez (2009, p.1).
El tipo de estudio de esta investigación es aplicativo (teórico) y responde por generalizar el concepto de área para cuerpos geométricos que están formados exclusivamente por polígonos regulares. Además, se utiliza el lenguaje de programación Python para corroborar el correcto funcionamiento de las fórmulas, así como un perfilamiento inédito del sentido aplicativo de la programación Matemática para el cálculo de área y volumen de solidos platónicos (Véase código fuente en Anexos).
La metodología empleada en este trabajo siguió las siguientes etapas:
- Revisión bibliográfica sobre los principales conceptos y propiedades ligadas a la teoría de solidos platónicos.
- Estudio de los métodos y procedimientos de cálculo de área y volumen de solidos platónicos.
- Formulación matemática de las demostraciones de fórmulas de áreas y volúmenes de los sólidos platónicos.
- Codificación en el lenguaje de alto nivel Python de los códigos fuentes de las fórmulas de áreas y volúmenes de los sólidos platónicos.
RESULTADOS Y DISCUSIÓN
Área y volúmenes de los sólidos platónicos
Los sólidos platónicos son cinco cuerpos geométricos que comparten un conjunto de características geométricas similares. También reciben el nombre de sólidos perfectos, poliedros platónicos y de cuerpos cósmicos entre otros. Los sólidos platónicos son poliedros regulares y convexos. En este sentido, se dice que: “Un poliedro es convexo cuando todo él está ubicado en el mismo semi espacio determinado por los planos que forman sus caras” (Romá, 2003).
De acuerdo con Quesada (2006, p.1) son cinco los sólidos platónicos: tetraedro, cubo (o hexaedro), octaedro, dodecaedro e icosaedro.
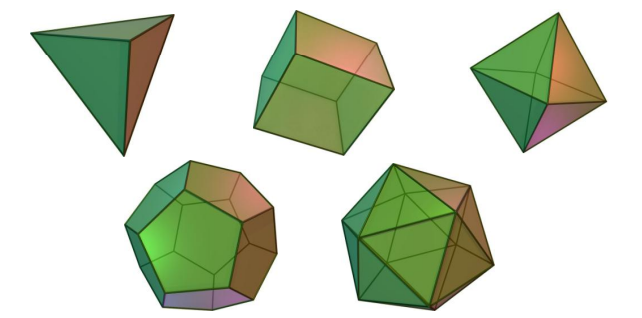
Citando a Romañach y Toboso (2016, p.2) las propiedades básicas comunes de los sólidos platónicos son:
- Todas las caras son polígonos regulares iguales.
- Todos los ángulos (diedros) son iguales.
- Todas las aristas tienen la misma longitud.
- En todos los vértices concurren el mismo número de caras y de aristas.
- Resultan ser fuertemente simétricos.
Tetraedro
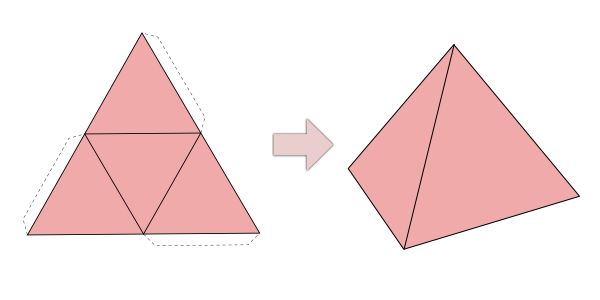
Teorema 1: El área del Tetraedro es donde A=√3 l2, donde l representa uno de los lados.
Demostración: Se sabe que el área del tetraedro estará conformada por las sumas de las cuatro áreas de los triángulos equilátero, es decir: donde es el área de una de las caras que conforman el tetraedro, luego el área del triángulo equilátero es
Entonces, haciendo una sustitución, se tiene
Simplificando, obtenemos el resultado
Teorema 2: El volumen del Tetraedro es donde representa uno de los lados.
Demostración: El volumen del tetraedro es
donde Ab representa el área de la base y la altura del tetraedro. El área de un triángulo equilátero es
Para calcular la altura del tetraedro, recordemos que el ortocentro o punto donde se cortan las alturas de un triángulo dista 1/3 de su longitud hasta el lado opuesto, es decir, ap/3 que equivale a un cateto del triángulo rectángulo. Este valor lo escribimos en función de la arista y obtenemos, que el valor del cateto menor es
y la hipotenusa, vale
Finalmente, el volumen es
Hexaedro o Cubo
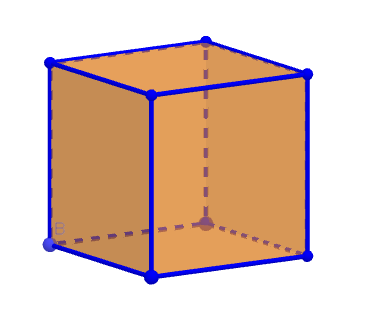
Las principales características del Hexaedro o Cubo de acuerdo con CEIP (2016, p.7) son:
- Posee caras que son cuadrados,
- Tiene vértices
- Tienes aristas
- Ángulos diedros que miden 90°.
Teorema 3: El área del cubo es A= 6l2, donde representa uno de los lados.
Demostración: El área de un cuadrado de lado l está dado por
como son 6 caras cuadradas, entonces, el área total es:

Teorema 4: El volumen del hexaedro es V=l3 ,donde representa uno de los lados.
Demostración: Se sabe que el volumen de un sólido en general es
donde representa el área de la base y la altura del cubo, la base del cubo es un cuadrado y su área es
Además, la altura es
entonces, su volumen es
En palabras de CEIP (2016, p.7) las principales características del Octaedro son:
- Tiene caras que son triángulos equiláteros
- Posee vértices.
- Tiene aristas
- Ángulos diedros que miden 109.47° .
Octaedro
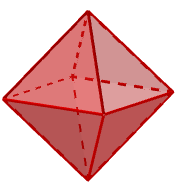
Teorema 5: El área del octaedro es A=2√3l2, donde l representa uno de los lados.
Demostración: El área de un triángulo equilátero de lado l está dado por
como son 8 caras triangulares, entonces, el área total es
Simplificando, resulta
Teorema 6: El volumen del octaedro , donde representa uno de los lados.
Demostración: El octaedro equivale a tener 2 pirámides cuadradas unidas por su base, además, el volumen de una pirámide cuadrada es
Por lo tanto, el doble de volumen de una pirámide cuadrada es lo mismo que el volumen de un octaedro, es decir
Realizando una sustitución, se tiene
sabiendo que la altura de la pirámide se expresa por
luego
Dodecaedro
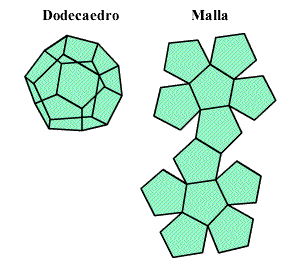
Según CEIP (2016, p.7) las principales características del Dodecaedro son:
- Posee caras que son pentágonos regulares.
- Tiene vértices
- Posee aristas
- Ángulos diedros que miden 116:56°.
Teorema 7: El área del Dodecaedro es , donde representa uno de los lados.
Demostración: El área de un pentágono regular de lado l está dado por
donde es la longitud del lado y la apotema, como son caras pentagonales, entonces, el área total es
como la apotema está dada por
luego, el área total es
Dodecaedro
Teorema 8: El volumen del Dodecaedro es
donde representa uno de los lados.
Demostración: El dodecaedro se descompone en pirámides.
El volumen de cada pirámide está determinado por
donde el área del pentágono regular es
Donde
sustituyendo estos valores en la fórmula del volumen de la pirámide, se tiene
ahora debemos de encontrar el valor de la altura de la pirámide (h), donde la apotema de la cara APC de una de la pirámide es
luego, aplicando el teorema de Pitágoras, obtenemos
luego el volumen total del dodecaedro es
Lo cual es equivalente a
Icosaedro
Las principales características del Icosaedro de CEIP (2016, p.7) son:
- Posee caras que son triángulos equiláteros.
- Tiene vértices
- Posee aristas
- Ángulos diedros que miden 138.19°.
Teorema 9: El área del icosaedro es A=5√3l2 donde representa uno de los lados.
Demostración: El área de un triángulo equilátero de lado l está dado por
como son 20 caras triangulares, entonces, el área total es
Icosaedro
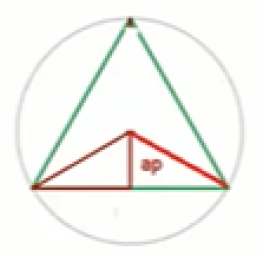
Teorema 10: El volumen del icosaedro es
donde representa uno de los lados.
Demostración: Tomando una cara del icosaedro, el segmento entre el centro de la cara y el punto medio de la arista es la apotema
Luego, el ángulo superior es 360/3=120°, luego el ángulo superior del triángulo rectángulo es 60 (por ser bisectriz), luego el ángulo basal es
luego, el área de un polígono regular es
el ángulo entre dos caras de un icosaedro es 138.19°
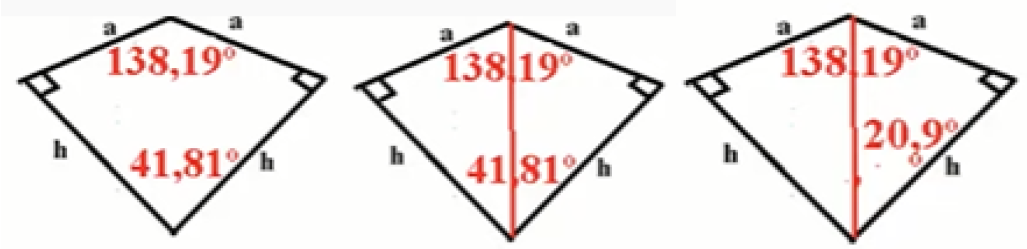
Luego
Sustituyendo
entonces el volumen de la pirámide es
y el volumen del icosaedro es
Los resultados obtenidos sobre el cálculo del área y volumen de los sólidos platónicos, son producto de la aplicabilidad de la teoría geométrica de polígonos regulares y sus combinaciones básicas, esto permitió obtener las fórmulas de áreas y volumen de los cincos solidos cósmicos o platónicos. Por otro lado, muestra la aplicación de resultados de polígonos regulares con la construcción de los sólidos.
Es necesario hacer referencia a la aplicabilidad de numerosas propiedades de los polígonos regulares en las demostraciones de los sólidos platónicos, su conexión intrínseca con la construcción de los cuerpos geométricos y la facilidad con que se demuestran las fórmulas de cálculo de áreas mediante una generalización del concepto de área de polígonos regulares.
Por otro lado, el estudio de los sólidos cósmicos, permite reconocer algunas particularidades específicas, entre ellas:
- En cada uno de los vértices de un sólido cósmico concurren el mismo número de caras y de aristas.
- Todas las aristas de un sólido cósmico tienen la misma longitud.
- Todos los ángulos diedros que forman las caras de un sólido cósmico entre sí son iguales.
- Los sólidos cósmicos verifican la famosa formula de Euler, es decir, V+C = A+2, donde V es el número de vértices; C número de caras y A número de aristas.
- Los sólidos cósmicos son los únicos cuerpos geométricos que cumplen dos propiedades propias, a saber: regularidad y convexidad.
Es importante señalar que se obtuvieron los siguientes resultados:
- Uso de la teoría geométrica para la obtención de fórmulas del cálculo de área y volumen para los cincos sólidos platónicos.
- Se desarrollaron 10 demostraciones sobre el área y volumen de solidos platónicos, mediante el desarrollo de la teoría de los polígonos regulares y la geometría.
- Todas las fórmulas de áreas de los sólidos plantónicos se derivan como consecuencia inmediata de las respectivas fórmulas de áreas de los objetos geométricos regulares según el número de lados.
- Todas las fórmulas de áreas y volúmenes dependen del valor de la magnitud del lado del solido platónico.
- Aplicación del paradigma funcional en la codificación y programación del lenguaje de alto nivel Python.
CONCLUSIONES
Las principales conclusiones del presente trabajo se pueden resumir por:
- Aplicación de técnicas geométricas para la obtención de las diversas fórmulas de áreas y volumen de los sólidos platónicos.
- Formulación de procedimientos para el desarrollo constructivo de teoremas geométricos referido al cálculo de áreas y volumen de los sólidos platónicos.
- Se induce la aplicación de la teoría trigonométrica como herramienta fundamental en la obtención de las fórmulas de áreas y volúmenes de los sólidos platónicos.
- Implementación de los algoritmos de fórmulas de áreas y volúmenes mediante la codificación en el lenguaje de alto nivel Python.
REFERENCIAS BIBLIOGRAFICAS
CEIP. (12 de Enero de 2016). Los cuerpos geometrícos - Junta de Andalucia. https://www.juntadeandalucia.es/averroes/centros-tic/21003232/helvia/sitio/upload/20__conoce_las_mates___cuerpos_geometricos.pdf
Gámez, C. (23 de Octubre de 2009). Consturccioones Geometrícas Fundamentales. https://archivos.csif.es/archivos/andalucia/ensenanza/revistas/csicsif/revista/pdf/Numero_23/CRISTINA_GAMEZ_1.pdf
Guirao, A. (24 de Noviembre de 2020). Sólidos Platónicos - Universidad de Murcia. https://www.um.es/phi/aguirao/EntreParticulas/PDF/2020%20nov24.pdf
Orozco, I. J. (2022). Acerca de la diagonal del Cuadrado. Revista de Divulgacion y Prensa, Farem-Chontales.
Quesada, C. (12 de Diciembre de 2006). Los sólidos platónicos - Departamento de Matemática UNAM . https://lya.fciencias.unam.mx/gfgf/ga20132/poliedros/arch5.pdf
Romá, J. D. (2003). Poliedros regulares: geometría descriptiva. Club Universitario.
Romañach, J., & Toboso, M. (12 de Mayo de 2016). Los sólidos platónicos y la proporción áurea (I). Relaciones y Series. http://www.diversocracia.org/docs/platonicos_aureos_I_.pdf
ANEXOS
Programación en Python
import math
from time import sleep
print()
print('M E N U P R I N C I P A L')
print()
def mostrar_menu(opciones):
print('Seleccione una opción:')
print()
for clave in (opciones):
print(f' {clave}) {opciones[clave][0]}')
def leer_opcion(opciones):
print()
while (a := input('Deme su Opción: ')) not in opciones:
print('Opción incorrecta, vuelva a intentarlo.')
return a
def ejecutar_opcion(opcion, opciones):
opciones[opcion][1]()
def generar_menu(opciones, opcion_salida):
opcion = None
while opcion != opcion_salida:
mostrar_menu(opciones)
opcion = leer_opcion(opciones)
ejecutar_opcion(opcion, opciones)
print()
def menu_principal():
opciones = {
'1': ('Area del Tetraedro :', AreaTetraedro),
'2': ('Volumen del Tetraedro :', VolumenTetraedro),
'3': ('Area del Cubo :', AreaCubo),
'4': ("Volumen del Cubo :", VolumenCubo),
'5': ("Area del Octaedro :", AreaOctaedro),
'6': ("Volumen del Octaedro :", VolumenOctaedro),
'7': ("Area del Dodecaedro :", AreaDodecaedro),
'8': ("Volumen del Dodecaedro :", VolumenDodecaedro),
'9': ("Area del Icosaedro :", AreaIcosaedro),
'10': ("Volumen del Icosaedro :", VolumenIcosaedro),
'11': ('Salir', salir) }
generar_menu(opciones, '11')
def AreaTetraedro():
print()
print("Datos del Tetraedro")
l=float(input("Deme el lado : "))
print()
print("El area es : ", math.sqrt(3)*l**2, " unidades cuadradas")
sleep(3)
pass
def VolumenTetraedro():
print()
print("Datos del Tetraedro")
l=float(input("Deme el lado : "))
print()
print("El Volumen es : ", math.sqrt(2)/12*l**3, " unidades cubicas")
sleep(3)
pass
def AreaCubo():
print()
print("Datos del Cubo")
l=float(input("Deme el lado : "))
print()
print("El área es : ", 6*l**2, " unidades cuadradas")
sleep(3)
pass
def VolumenCubo():
print()
print("Datos del Cubo")
l=float(input("Deme el lado : "))
print()
print("El volumen es : ", l**3, " unidades cubicas")
sleep(3)
pass
def AreaOctaedro():
print()
print("Datos del Octaedro")
l=float(input("Deme el lado : "))
print()
print("El área es : ", 2*math.sqrt(3)*l**2, " unidades cuadradas")
sleep(3)
pass
def VolumenOctaedro():
print()
print("Datos del Octaedro")
l=float(input("Deme el lado : "))
print()
print("El volumen es : ", math.sqrt(2)/3*l**3, " unidades cubicas")
sleep(3)
pass
def AreaDodecaedro():
print()
print("Datos del Dodecaedro")
l=float(input("Deme el lado : "))
print()
print("El área es : ", math.sqrt(25+10*math.sqrt(5))*3*l**2, " unidades cuadradas")
sleep(3)
pass
def VolumenDodecaedro():
print()
print("Datos del Dodecaedro")
l=float(input("Deme el lado : "))
print()
print("El volumen es : ", (15+7*math.sqrt(5))/4*l**3, " unidades cubicas")
sleep(3)
pass
def AreaIcosaedro():
print()
print("Datos del Icosaedro")
l=float(input("Deme el lado : "))
print()
print("El área es : ", 5*math.sqrt(3)*l**2, " unidades cuadradas")
sleep(3)
pass
def VolumenIcosaedro():
print()
print("Datos del Icosaedro")
l=float(input("Deme el lado : "))
print()
print("El volumen es : ", 5/12*(3+math.sqrt(5))*l**3, " unidades cubicas")
sleep(3)
pass
def salir():
print('Saliendo del Sistema')
if __name__ == '__main__':
menu_principal()
© 2023 Revista Científica de FAREM-Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.

