Estudio sobre relaciones de equivalencia en los distintos dominios numéricos con una y dos operaciones
Estudio sobre relaciones de equivalencia en los distintos dominios numéricos con una y dos operaciones
Arnoldo Abraham Herrera Herrera
Universidad Nacional Autónoma de Nicaragua, Maangua. UNAN-Managua, Nicaragua
https://orcid.org/0000-0003-3001-8861
arnoldo.herrera@unan.edu.ni
RECIBIDO
16/10/2023
ACEPTADO
02/04/2024
RESUMEN
Este trabajo aborda el estudio de las relaciones de equivalencia en los distintos dominios numéricos que involucran una y dos operaciones. Es conocido que las relaciones de equivalencia desempeñan un papel esencial en el análisis y estudio de los conjuntos numéricos, a su vez permiten establecer conexiones entre elementos dentro de un conjunto dado. El objetivo principal de este estudio es proporcionar una comprensión profunda de las relaciones de equivalencias en la construcción de diversos dominios (N⊆Z⊆Q⊆R), asimismo examinar cómo influyen en su estructura y en sus propiedades. Esta jerarquía conjuntista inclusiva muestra cómo los conjuntos numéricos se construyen de manera gradual, ampliando las propiedades y características de los conjuntos anteriores. La construcción de estos dominios es fundamental en matemáticas y tiene aplicaciones en diversos campos, desde la aritmética básica hasta el análisis matemático avanzado. Además, se explorarán las definiciones y aplicaciones de estas relaciones de equivalencia, y se investiga las implicaciones que tienen en la demostración de distintos teoremas. Por otra parte, a través de este análisis, se busca contribuir al avance de la teoría de conjuntos numéricos, brindando herramientas conceptuales útiles para el estudio de estos dominios. También se espera que este artículo proporcione una base sólida para futuras investigaciones en el campo de las relaciones de equivalencias dentro de los distintos dominios numéricos, asimismo que las propiedades de una relación de equivalencia mediante las operaciones de unión e intersección utilizando relaciones de equivalencia y envoltura transitiva generen un mayor entendimiento de cada estructura y en general de estos sistemas matemáticos fundamentales.
PALABRAS CLAVES
Relaciones de equivalencia; dominios numéricos; estructura; operaciones; propiedades.
ABSTRACT
This paper deals with the study of equivalence relations in different numerical domains involving one and two operations. It is known that equivalence relations have an essential role in the analysis and study of numerical sets, in turn they allow to establish connections between elements within a given set. The main objective of this study is to provide an in-depth understanding of equivalence relations in the construction of various domains (N⊆Z⊆Q⊆R) and to examine how they influence their structure and properties. This inclusive conjunctive hierarchy shows how numerical sets are constructed in a stepwise manner, extending the properties and characteristics of previous sets. The construction of these domains is fundamental in mathematics and has applications in a variety of fields, from basic arithmetic to advanced mathematical analysis. In addition, the definitions and applications of these equivalence relations will be explored, and the implications they have in the proof of different theorems are investigated. On the other hand, through this analysis, we seek to contribute to the advancement of the theory of numerical sets, providing useful conceptual tools for the study of these domains. It is also expected that this article will provide a solid basis for future research in the field of equivalence relations within the different numerical domains, likewise that the properties of an equivalence relation by means of the union and intersection operations using equivalence relations and transitive envelopes will generate a better understanding of each structure and in general of these fundamental mathematical systems.
KEYWORDS
Equivalence relations; number domains; structure; operations; properties.
INTRODUCCIÓN
Este trabajo se enfoca en la importancia de las relaciones de equivalencia en la matemática y su relevancia en la comprensión de la estructura y propiedades de los sistemas numéricos, desde situaciones primarias de la vida humana, hasta su cristalización técnica en el área de la Matemática actual.
En una primera etapa se investigó acerca de la identificación de eventos que permitiesen inferir la determinación sobre relaciones que fuesen de equivalencia, conservando así una perspectiva de aplicación directa del concepto.
El segundo trayecto consistió en formar el conglomerado de conceptos adjuntos al de relación de equivalencia (clases de equivalencia, partición de un conjunto, conjunto cociente) y la determinación de su aplicación en diversos contextos. Mediante la aplicación de estas relaciones, se pueden establecer patrones y propiedades que ayudan a simplificar problemas y demostrar teoremas que son piedras angulares de la construcción de cada dominio numérico.
Las relaciones de equivalencias en los distintos dominios numéricos son objeto de estudio en diversos campos científicos, como: Lógica y Estructuras Numéricas. Estas relaciones permiten establecer conexiones entre diferentes elementos dentro de un conjunto dado, así como para hacer conexión con otros conjuntos. El análisis de las relaciones de equivalencia en los dominios numéricos con una y dos operaciones es relevante para comprender la estructura y propiedades de estos sistemas numérico.
En principal propósito de este trabajo es mostrar la utilidad de las relaciones de equivalencias en los distintos dominios numéricos, prestando especial atención en aquellos que involucran una y dos operaciones. En primera instancia se explora cómo estas relaciones se definen y se aplican en estos contextos, y luego se examina cómo afectan la estructura y propiedades de los conjuntos numéricos correspondientes. Por otra parte, se estudian las implicaciones de estas relaciones de equivalencia en la resolución de teoremas dentro de cada dominio, por ejemplo: En el conjunto de números enteros, una relación de equivalencia común es la congruencia módulo , concretamente la relación es a≡b mod 3. Esto significa que dos enteros a y b son equivalentes si tienen el mismo residuo al ser divididos por 3.
Además, se busca proporcionar una visión profunda y sistemática de las relaciones de equivalencias en los distintos dominios numéricos con una y dos operaciones, en consecuencia, ayudará al lector en el avance del estudio de la teoría de conjuntos numéricos y brindar herramientas conceptuales útiles para comprender su gran utilidad.
Alrededor de esta temática principal surgen las interrogantes: ¿Qué importancia tienen las relaciones de equivalencia en la construcción de los distintos dominios numéricos y cómo se pueden realizar operaciones con una o dos relaciones de equivalencia en un conjunto dado?
Fundamentación teórica
Luego de haber efectuado una revisión de la bibliografía y webgrafía sobre las investigaciones asociadas al concepto de relación de equivalencia, se encontró la siguiente información:
El libro “Álgebra I” de Rojo (1996), presenta un tratado riguroso sobre la definición de relación de equivalencia, así como su gran utilidad en la construcción de los distintos dominios numéricos: naturales (N), enteros (Z), racionales (Q) y reales (R). Este autor también presenta demostraciones de teoremas que tienen una repercusión imprescindible en el estudio de estructuras numéricas complejas, a su vez enfatiza en el tratado de propiedades que se cumplen dentro de cada uno de estos dominios.
El texto “Álgebra y Teoría de números” (Koulikov, 1982) ayudó a estudiar los sistemas algebraicos en general, así como contribuir a la formación de nuestra cultura algebraica, debido a que se necesita una agudeza cognitiva para la comprensión profunda de la semiótica, psicología, historia y didáctica de la matemática elemental.
Asociados a las investigaciones antes mencionadas, está la de Revilla (2010) titulada “Cursos Matemáticos - Relaciones de Equivalencia”, utiliza conceptos y teoremas correspondientes a la resolución de problemas conectados con la vida cotidiana, y de la misma manera, plantear y resolver algunos ejercicios aplicados que presentan cierto grado de dificultad. El estudio concluyó mostrando que el estudiante debe poseer cualidades y habilidades en Matemática, puesto que estas son el eje principal para el desarrollo auténtico y significativo en cualquier lugar de trabajo. Por tal razón, afirman que es necesario proporcionar métodos adecuados para lograr un excelente aprendizaje.
Curveira y Bravo (2013) en su trabajo “Tratamiento de conceptos matemáticos, su repercusión en el proceso de formación profesional inicial”, estudian la formación de habilidades en los estudiantes en la asignatura de Matemática General, a partir de las aclaraciones de los tipos de conceptos y las distintas relaciones matemáticas entre estos.
Antes de abordar los principales teoremas y operaciones de las relaciones de equivalencia en cada dominio numérico, es necesario proporcionar ciertos conceptos y definiciones tomadas de Rojo (1996, p.1-80) y Herrera y Cisneros (2023), las cuales servirán como base para comprender de mejor forma la temática en cuestión.
Conjunto: Dada una colección X de elementos, si x es un elemento de X escribiremos x ∈ X, mientras que si no pertenece a X escribiremos x ∉ X . Si P es una propiedad, indicaremos por P(x) el hecho de que P sea cierta para el elemento x. Con esta notación, un conjunto X es una colección de elementos x tales que exista una propiedad P de modo que x ∈ X si y sólo si P(x) es verdadera.
Par ordenado: El par ordenado (a, b) es el conjunto cuyos elementos son {a} y {a,b}. Es decir (a,b) = {{a}, {a, b}}.
a y b son la primera y segunda componente del par ordenado, respectivamente.
Producto cartesiano: El producto cartesiano de los conjuntos A y B es el conjunto cuyos elementos son todos los pares ordenados cuya primera componente pertenece a A y la segunda a B. Simbólicamente,
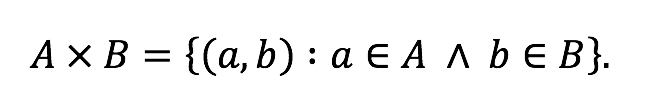
Relación: Una relación entre A y B es todo subconjunto del producto cartesiano A x B. En símbolos,
R es una relación definida en 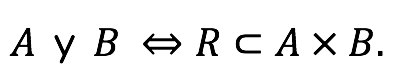
Relaciones definidas en un conjunto: Supóngase que R es una relación entre A y B, donde B=A. En este caso se dice que la relación está definida en A, y se identifica con un subconjunto de A2=A×A.
R es una relación definida en
![]()
Relación de equivalencia: La relación ~⊂A2 es de equivalencia en A si, y solo si, es reflexiva, simétrica y transitiva.
Reflexividad: Todo elemento de A está relacionado consigo mismo.
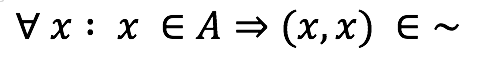
Simetría: Si un elemento está relacionado con otro, entonces este está relacionado con el primero.
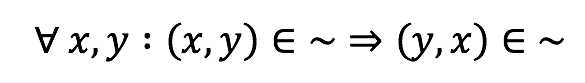
Transitividad: Si un elemento está relacionado con otro y este está relacionado con un tercero, entonces el primero está relacionado con el tercero.
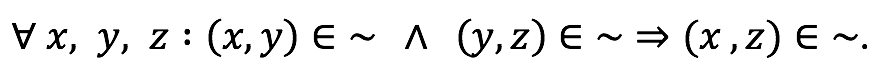
Clase de equivalencia: Clase de equivalencia del elemento a ∈ A es el conjunto de todos los elementos de A que están relacionados con a.
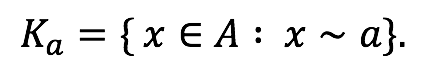
Conjunto de Índices: Es el conjunto formado por todos los elementos que han sido seleccionados como representantes de cada clase de equivalencia.
Partición: Sean dos conjuntos A ≠ ∅ e I ≠ ∅ tales que, cualquiera que sea el elemento u ∈ I, existe un subconjunto Ku ⊂ A. El conjunto {Ku∶u ∈ I} es una partición de A si y solo si
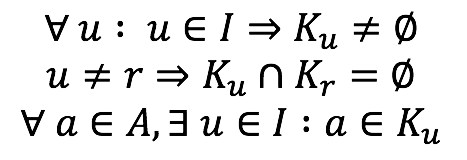
El conjunto I se llama conjunto de índices.
Conjunto cociente: El conjunto formado por las clases de equivalencia se llama conjunto cociente de A por la relación de equivalencia ~, y la notación es
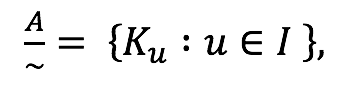 donde I es el conjunto de índices.
donde I es el conjunto de índices.
MATERIALES Y MÉTODOS
En esta sección se describe la metodología utilizada para deducir, construir y ejemplificar las relaciones de equivalencia en el ámbito escolar y en la vida cotidiana.
Etapas de investigación:
La metodología empleada en este trabajo siguió las siguientes etapas:
- Revisión del estado del arte sobre el concepto de relación de equivalencia: se lleva a cabo una revisión exhaustiva de la literatura existente sobre el concepto de relación de equivalencia en matemáticas. Esto implica analizar diferentes definiciones, ejemplos y aplicaciones de relaciones de equivalencia en diversas áreas de las matemáticas, así como también estudiar cómo se han utilizado en la investigación previa.
- Estudio de diversos procedimientos matemáticos sobre la definición conceptual y formal de relación de equivalencia: Aquí se profundiza en el estudio de los fundamentos teóricos de las relaciones de equivalencia, incluyendo su definición formal, propiedades y características. Se exploran conceptos clave como la reflexividad, simetría y transitividad, así como el análisis de diferentes maneras de representar y trabajar con relaciones de equivalencia.
- Estudio, demostración y justificación de los principales teoremas y propiedades que utilizan las relaciones de equivalencia en diversos dominios numéricos: Enfocado en comprender y demostrar teoremas importantes relacionados con las relaciones de equivalencia en diferentes dominios numéricos.
- Análisis y tratamiento sobre una o dos operaciones mediante relaciones de equivalencia: En este momento, se exploran cómo las relaciones de equivalencia pueden utilizarse para analizar y tratar una o dos operaciones específicas en un conjunto dado. Se examinan las propiedades de estas operaciones bajo la acción de las relaciones de equivalencia y se analizan posibles aplicaciones y generalizaciones.
Este trabajo se enmarca en una investigación aplicada, cuyo objetivo es la aplicación y consolidación del concepto de relación de equivalencia en diversos dominios numéricos, demostrando su utilidad en operaciones simples o combinadas.
También, se utilizó el método de inducción para buscar y registrar teoremas que se relacionan con las condiciones de la definición de relaciones de equivalencia.
El método de implicación directa es utilizado para demostrar las afirmaciones condicionales. Este método se utiliza para probar las distintas proposiciones sobre las relaciones de equivalencia, que tiene la forma “Si P, entonces Q”, donde es la hipótesis y es la conclusión. La idea esencial es demostrar que cuando la hipótesis es verdadera, la conclusión también debe ser verdadera.
El método analítico fue claramente utilizado al examinar la precisión y efectividad de la definición de relación de equivalencia en el funcionamiento de las demostraciones de los teoremas que la involucran. Una buena definición es "justificada" por los teoremas que pueden probarse con ella, al igual que la prueba del teorema está justificada apelando a una definición dada anteriormente”.
La síntesis, como método cognoscitivo opuesto al análisis, se ve reflejada en la aparición gradual de otros conceptos matemáticos que, a partir de la definición de relación de equivalencia, fueron incorporándose a estructuras algebraicas más completas.
Este trabajo presenta ejemplificaciones originales y genuinas de conceptos matemáticos, como la construcción del conjunto cociente y la función canónica, que se relacionan con la definición de relación de equivalencia y su aplicación en distintos contextos.
RESULTADOS Y DISCUSIÓN
Las relaciones de equivalencia se observan en las diferentes situaciones de la vida y en los distintos niveles educativos, tanto en ejemplos sencillos como complejos, de acuerdo con la temática en estudio. A continuación, se presentan los siguientes casos relevantes considerando información imprescindible de los textos Joyce (1996), Rojo (1996) y Koulikov (1982):
Construcción de los números enteros
Para la construcción de los números enteros ![]() , se parte de una relación definida en el conjunto de pares ordenados de números naturales
, se parte de una relación definida en el conjunto de pares ordenados de números naturales ![]() , la relación está definida por:
, la relación está definida por:
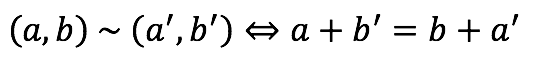
Reflexividad
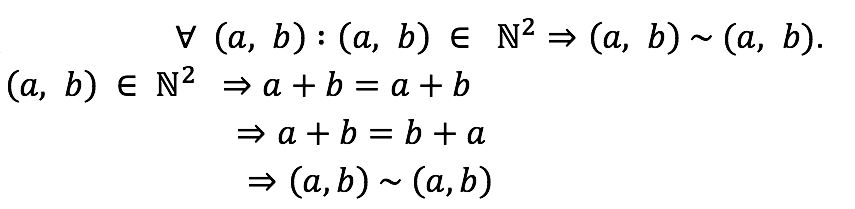
Reflexividad de la igualdad de números naturales.
Conmutatividad de la adición en N.
Definición de relación.
Simetría
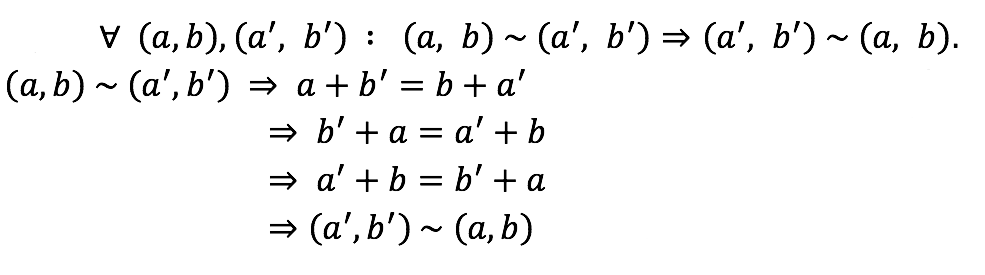
Definición de la relación e hipótesis.
Conmutatividad de la adición en N.
Simetría de la igualdad de números naturales.
Definición de la relación.
Transitividad
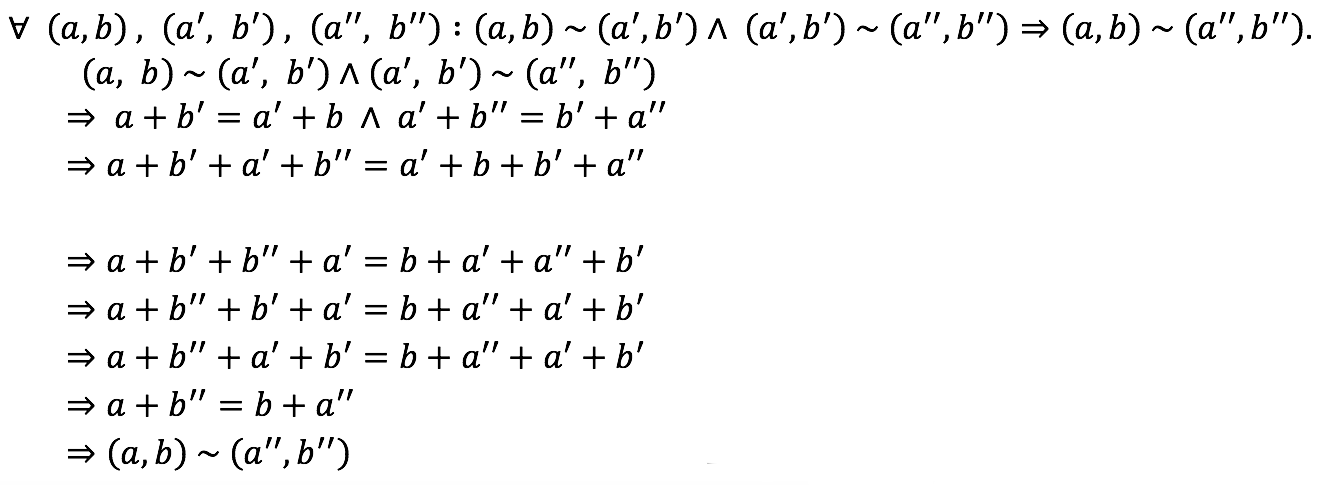
Definición de la relación e hipótesis.
Compatibilidad de la igualdad respecto a la adición en N.
Conmutatividad de la adición en N.
Conmutatividad de la adición en N.
Conmutatividad de la adición en N.
Ley cancelativa de la adición en N.
Definición de la relación.
- Los pares (3,4) y (6,7) están relacionados porque 3 + 7 = 4 + 6 = 10.
- Los pares (5,4) y (8,7) están relacionados porque 5 + 7 = 4 + 8 = 12.
Sea I el conjunto de índices:
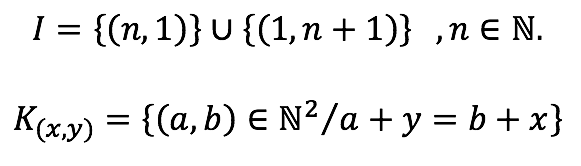
Algunos ejemplos de clases de equivalencias
Para determinar si dos pares de números enteros están relacionados bajo esta definición, simplemente se suman los elementos correspondientes (extremos y medios) de cada par y se verifica si es igual en ambos casos. Si lo es, entonces los pares están relacionados bajo esta relación de equivalencia; de lo contrario, no lo están.
La clase K(1, 3) está formada por todos los pares (a, b) que cumplen a + 3 = b + 1, es decir todos los pares cuya segunda componente es: la primera componente más 2 : b = a + 2.
La clase K(2, 1) está formada por todos los pares (x, y) que cumplen x + 1 = y + 2, es decir todos los pa res cuya segunda componente es: la primera componente disminuida en 1 : y = x - 1.
Conjunto cociente
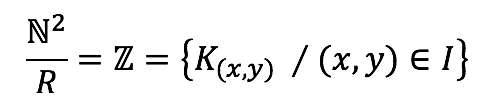
- Para la construcción de los números racionales Q se parte de una relación definida en Z × Z*, mediante:
Nota: 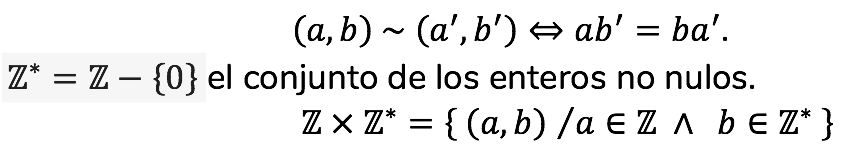
Esta relación de equivalencia establece que dos pares ordenados de números enteros son equivalentes si su producto cruzado es igual. Esta relación es fundamental para la construcción de los números racionales, ya que permite identificar clases de equivalencia que luego pueden ser utilizadas para definir las operaciones básicas sobre los racionales.
A continuación, se verifica que la relación es de equivalencia.
Reflexividad
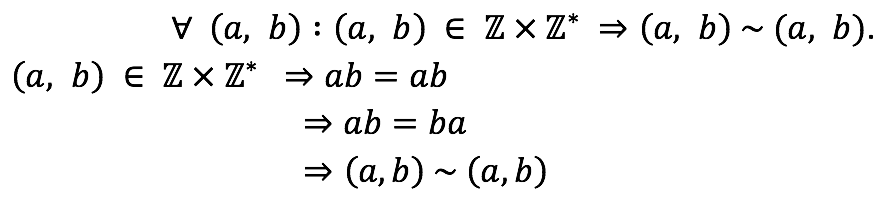
Reflexividad de la igualdad de números enteros.
Conmutatividad del producto en Z.
Definición de la relación.
Simetría
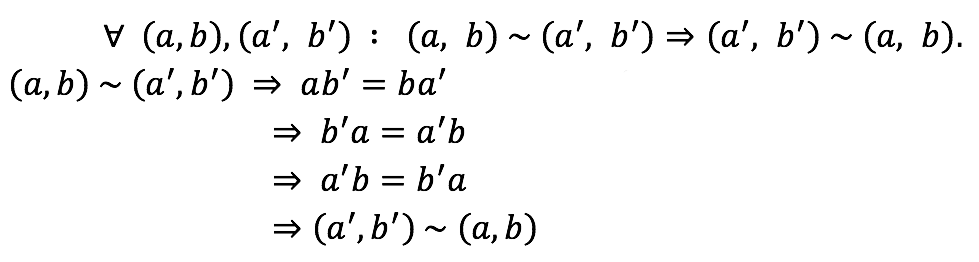
Definición de la relación e hipótesis.
Conmutatividad del producto en Z.
Simetría de la igualdad.
Definición de la relación.
Transitividad
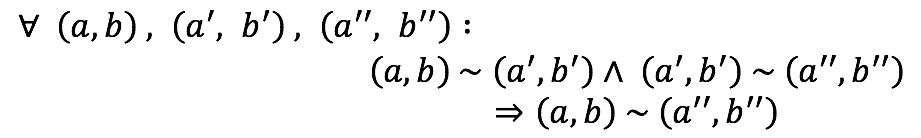
Partiendo de:
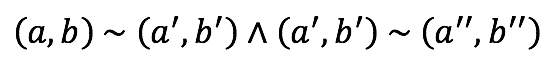
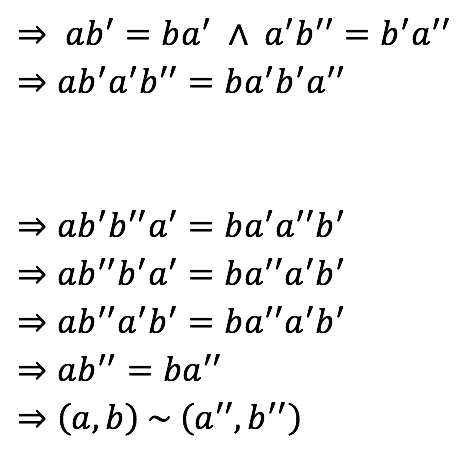
Definición de la relación e hipótesis.
Compatibilidad de la igualdad respecto al producto en Z.
Conmutatividad del producto en Z.
Conmutatividad del producto en Z.
Conmutatividad del producto en Z.
Ley cancelativa del producto en Z.
Definición de la relación.
Ejemplos:
Los pares (-2, -4) y (-1,-2) están relacionados, porque (-2) ⋅ (-2) = (-4) ⋅ (-1) = 4
Los pares (3,1) y (6,2) están relacionados, debido a que 3 ⋅ 2 = 1 ⋅ 6 = 6
Sea J el conjunto de índices:
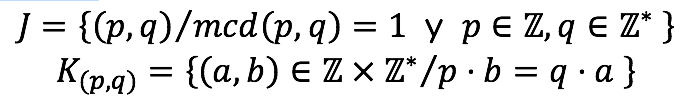
Algunos ejemplos de clases de equivalencias
- La clase K(1,2) está formada por todos los pares (a, b) que cumplen 1 ⋅ b = 2 ⋅ a, es decir todos los pares cuya segunda componente es: dos veces la primera componente: b = 2 ⋅ a.
- La clase K(0,1) está formada por todos los pares (x, y) que cumplen 1 ⋅ x = y ⋅ 0, esto es todos los pares cuya primera componente es cero.
Cada clase de equivalencia en el contexto de una relación de equivalencia entre pares de números enteros corresponde a un conjunto de pares que cumplen una condición específica. Esta condición específica está determinada por la relación de equivalencia que se ha definido.
Conjunto cociente:
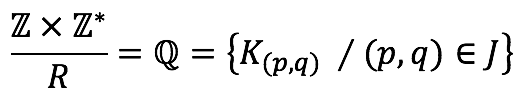
Así, el conjunto cociente estaría formado por las clases de equivalencia, donde cada clase representa un conjunto de pares de números enteros relacionados bajo la relación de equivalencia R.
Para la construcción de los números reales R se utilizan las cortaduras de Dedekind
Definición.
El subconjunto A ⊂ Q es una cortadura si y sólo si verifica
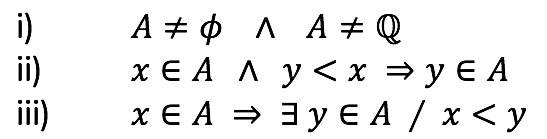
Se define Qc como el conjunto de todas las cortaduras.
En Qc se define la siguiente relación
![]()
Reflexividad:
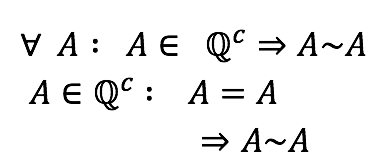
Igualdad de conjuntos.
Definición de la relación.
Simetría:
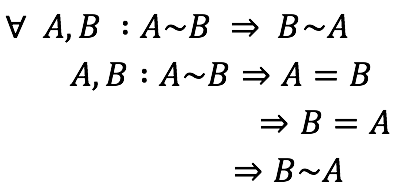
Definición de la relación e hipótesis.
Simetría de la igualdad de conjuntos.
Definición de la relación.
Transitividad
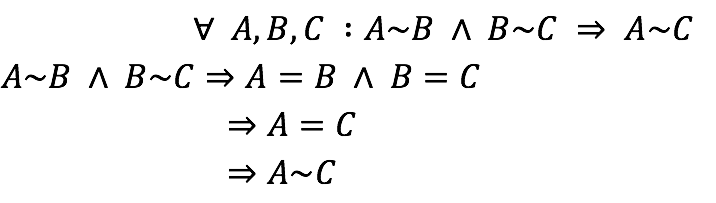
Definición de la relación e hipótesis.
Transitividad de la igualdad de conjuntos.
Definición de la relación.
- Otra variante muy interesante para la construcción de los números reales son las sucesiones de Cauch
La construcción de los números reales mediante las sucesiones de Cauchy se basa en la idea de considerar cada sucesión de Cauchy como un representante de un número real. Dos sucesiones de Cauchy que convergen al mismo límite se consideran equivalentes y representan el mismo número real. Esta es una relación de equivalencia basada en la convergencia de sucesiones.
Definición
Una sucesión es una función o aplicación, cuyo dominio es el conjunto de los enteros positivos o bien el conjunto de los números naturales y su codominio es cualquier conjunto.
![]()
donde A es cualquier conjunto.
Sucesión racional
Una sucesión racional es una función o aplicación de N a Q.
Es decir 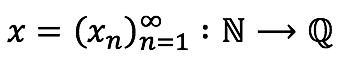
donde
![]()
El conjunto de las sucesiones racionales se denota por Q∞.
Si
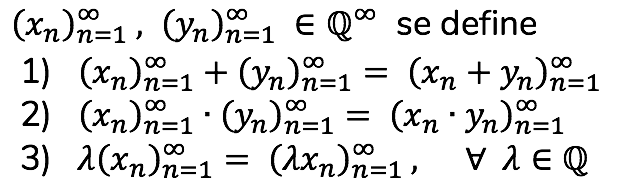
Definición
Sea
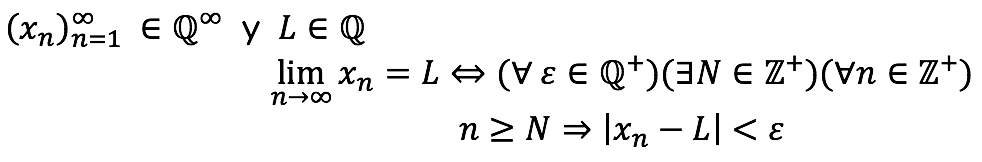
Sucesiones de Cauchy
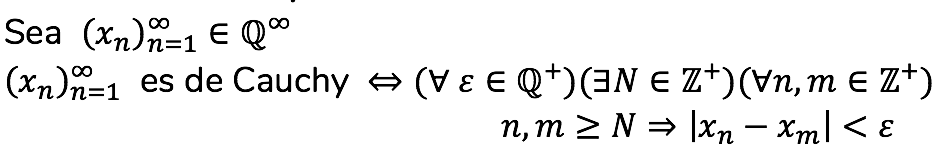
Sea F el conjunto de todas las sucesiones ![]() que son de Cauchy.
que son de Cauchy.
En F se define la siguiente relación 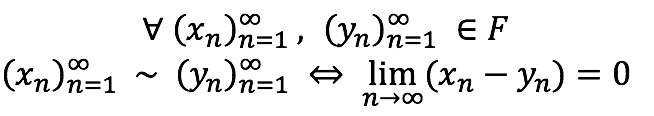
Entonces, esta relación de equivalencia establece que dos secuencias son equivalentes si la diferencia entre los términos correspondientes de las secuencias converge a cero cuando tiende a infinito.
Reflexividad
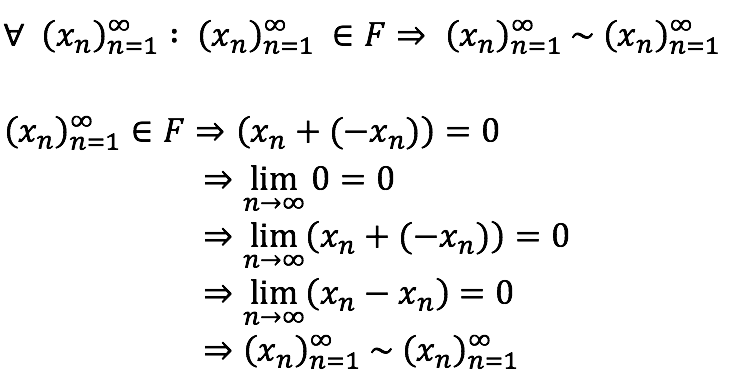
Suma de sucesiones opuestas.
Propiedad de límite.
Sustitución
Propiedad de la adición.
Definición de la relación.
Simetría
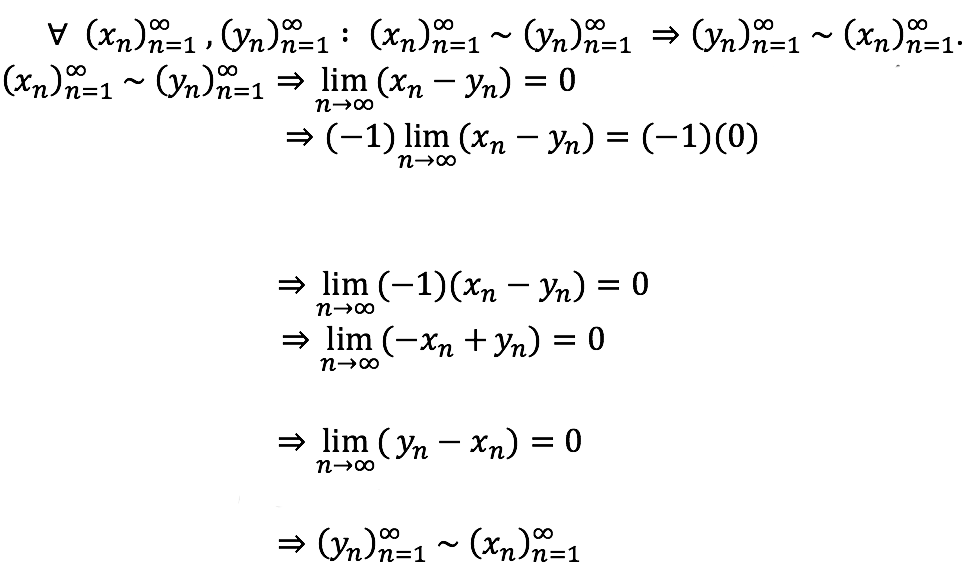
Definición de relación.
Compatibilidad de la igualdad respecto al producto.
Propiedad de límite
Producto de sucesiones por un escalar.
Conmutatividad de la adición en el conjunto de las sucesiones.
Definición de la relación.
Transitividad
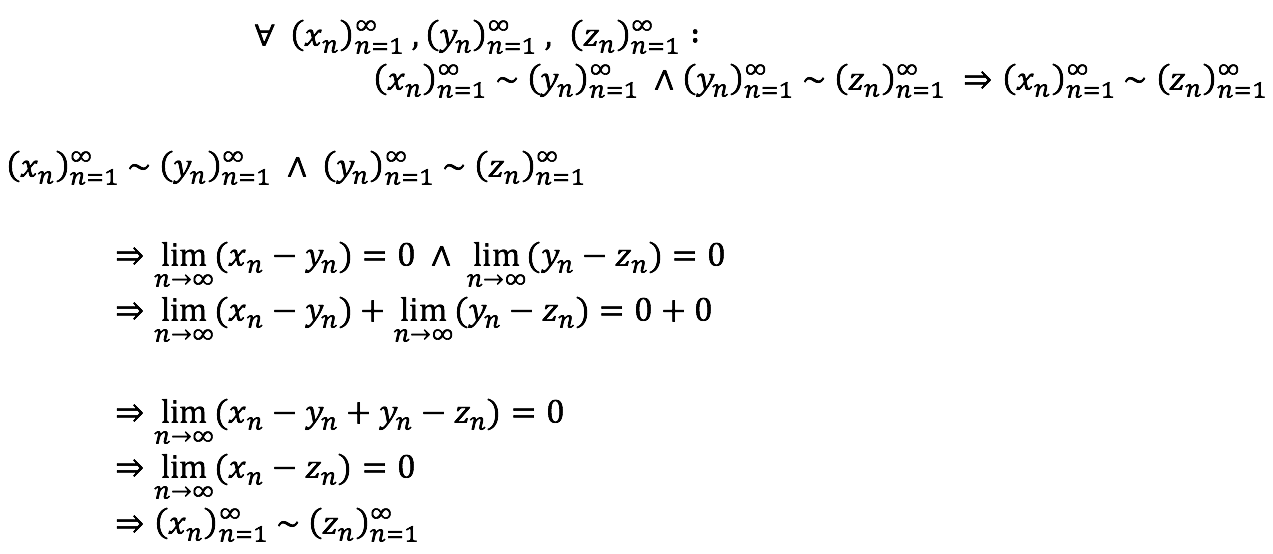
Definición de relación.
Compatibilidad de la igualdad respecto a la adición.
Propiedad de límite.
Adición de sucesiones opuestas.
Definición de la relación.
Para la construcción de los números complejos C, se parte de una relación definida en el conjunto de todos los pares ordenados de números reales R2. La cual está determinada por:
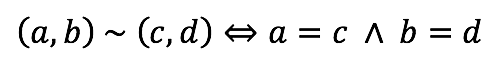
Reflexividad
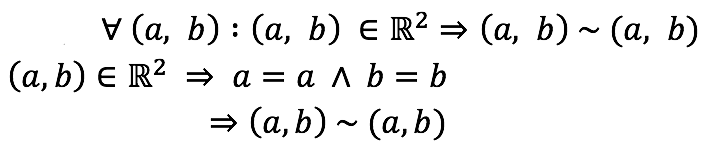
Reflexividad de la igualdad de números reales.
Definición de la relación.
Simetría
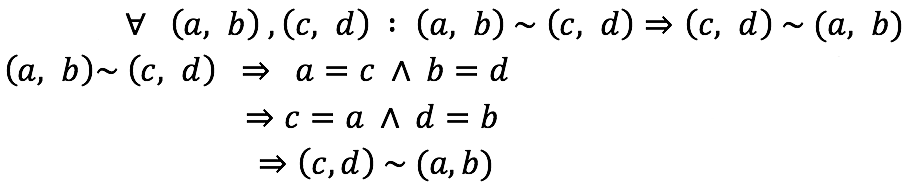
Definición de la relación e hipótesis.
Simetría de la igualdad de números reales.
Definición de relación.
Transitividad
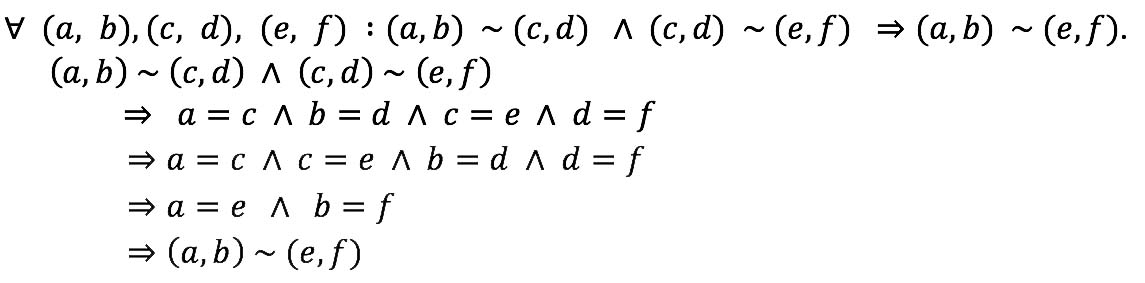
Definición de la relación e hipótesis.
Conmutatividad de la conjunción.
Transitividad de la igualdad de números reales.
Definición de la relación.
Operaciones con relaciones de equivalencia
Sea A un conjunto no vacío y sea Eq el conjunto de todas las relaciones de equivalencia definidas en el conjunto A. Es interesante preguntarse ¿La intersección de dos relaciones de equivalencia es una relación de equivalencia? La respuesta es positiva, como se muestra a continuación.
Intersección entre relaciones de equivalencia
Primero se debe asegurar que R1 ∩ R2 ≠ ∅, esto es cierto porque R1 y R2 son relaciones reflexivas.
Sean R1, R2 ∈ Eq demostrar que R1 ∩ R2 ∈ Eq
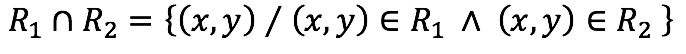
Se probarán las tres propiedades:
Reflexividad
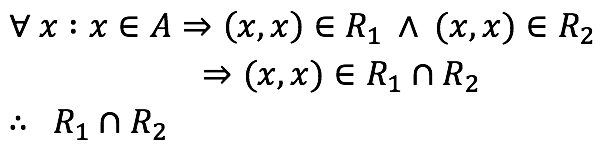
Propiedad reflexiva de R1 y R2
Definición de intersección
cumple la propiedad de reflexividad
Simetría
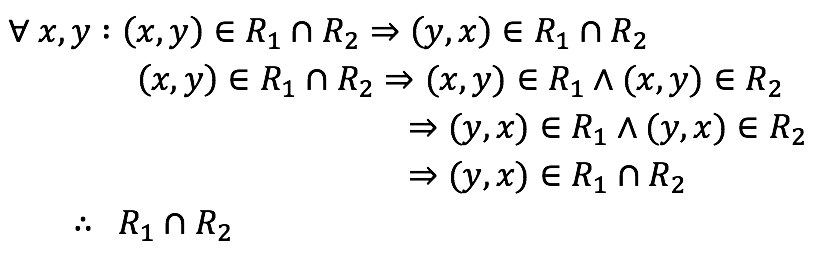
Definición de intersección
Simetría de R1 y R2
Definición de intersección
cumple la propiedad de simetría
Transitividad
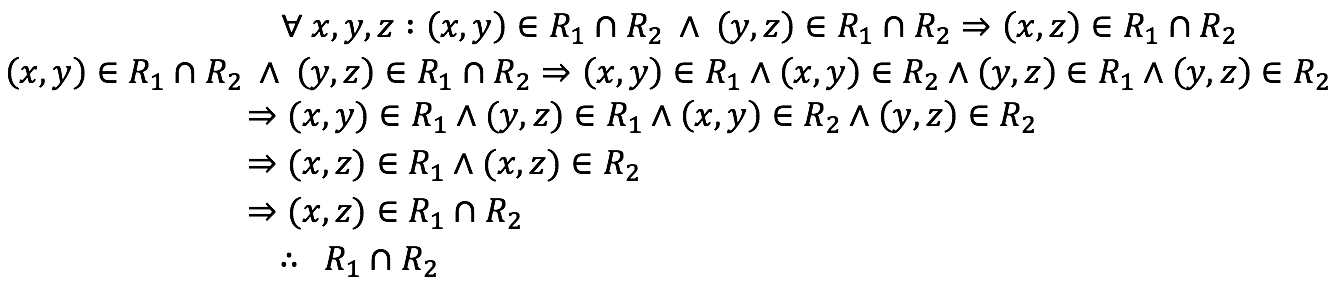
Conmutatividad de
Transitividad de R1 y R2
Definición de intersección
cumple la propiedad de transitividad
De este modo se demuestra que R1 ∩ R2 es una relación de equivalencia, es decir, R1 ∩ R2 ∈ Eq .
Generalización de intersección entre relaciones de equivalencia
El resultado anterior se puede generalizar para la intersección de n relaciones de equivalencia, definidas en un conjunto A, es decir
Si R1, R2 ,…,Rn ∈ Eq , entonces ![]()
La demostración es, en esencia análoga, a lo anterior.
Reflexividad
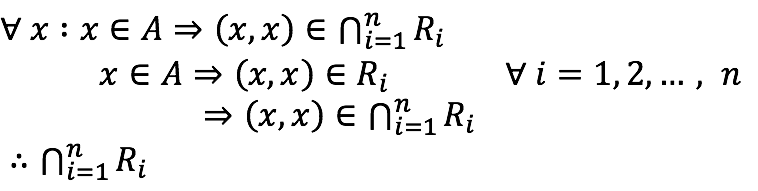
cumple la propiedad de reflexividad
Simetría
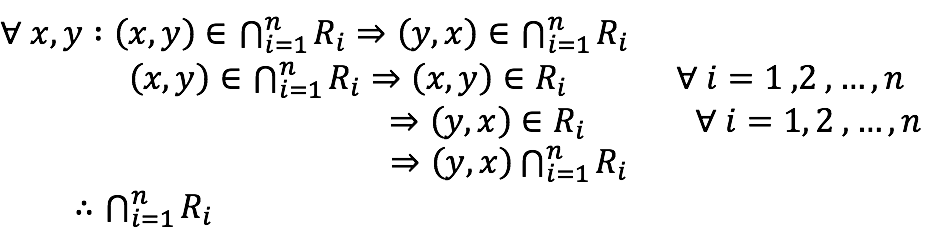
cumple la propiedad de simetria
Transitividad
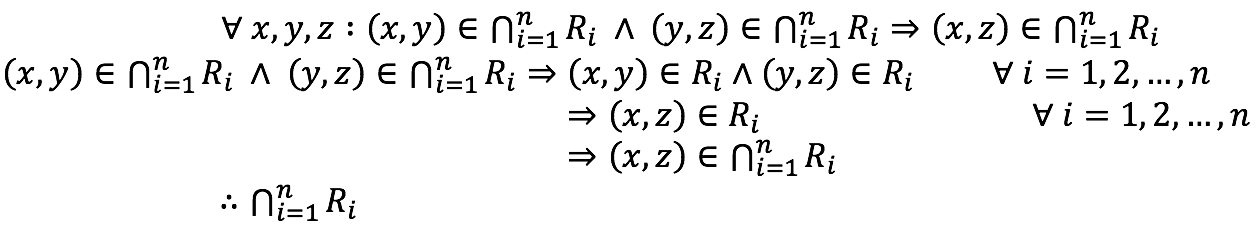
cumple la propiedad de transitiva
Comprobando así que 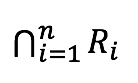 es una relación de equivalencia, es decir
es una relación de equivalencia, es decir ![]()
Unión entre relaciones de equivalencia
De manera natural surge la siguiente pregunta: ¿La unión de dos relaciones de equivalencia es una relación de equivalencia?
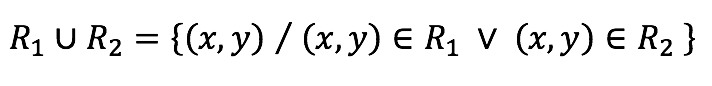
Mediante un contraejemplo se comprueba que en general la unión de relaciones de equivalencia no es una relación de equivalencia.
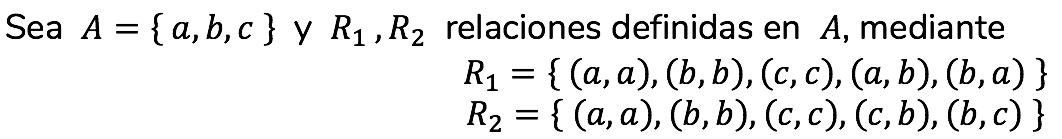
Se verifica con facilidad, que R1 y R2 son relaciones de equivalencia.
Por definición de unión se tiene que
![]()
Analizando se observa que cumple las propiedades de reflexividad y simetría, sin embargo, falla la transitividad, pues, por ejemplo
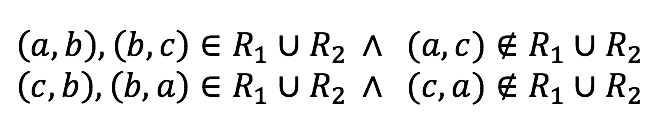
concluyendo que R1 ∪ R2 no es una relación de equivalencia.
Una forma de reparar este inconveniente es mediante la introducción del concepto de envoltura transitiva de una relación.
Si R1 y R2 son relaciones de equivalencia, entonces R1 ∪ R2 es una relación reflexiva y simétrica porque ∆A ⊂ R1 ∪ R2 y (R1 ∪ R2 )-1 = R1-1 ∪ R21 ⊂ R1 ∪ R2 . En el ejemplo se determinó que en general R1 ∪ R2 no es una relación de equivalencia porque falla la transitividad. Necesitando de la siguiente propiedad.
Propiedad:
Sea R una relación, entonces ![]() es transitiva.
es transitiva.
Demostración
Suponiendo que (a, b) y (b, c) ![]() , entonces existen x1,x2,…,xm ∈ A y y1, y2,…,yn ∈ A tales que
, entonces existen x1,x2,…,xm ∈ A y y1, y2,…,yn ∈ A tales que
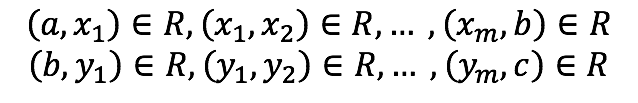
entonces existen x1,x2,…,xm , y1, y2,…,yn ∈ A tales que
![]()
lo cual significa que (a, c) ∈ Rp, para cierto p ∈ N.
Definición: La envoltura transitiva de una relación R es la menor (en el sentido de inclusión) relación transitiva 〈R〉 que contiene a R.
Propiedad: 〈R〉= R ∪ (R ∘ R) ∪… es la envoltura transitiva de R.
Demostración
Sea S una relación transitiva que contiene a R, se debe probar que ![]() ⊂ S. Para ello se necesitan dos cosas:
⊂ S. Para ello se necesitan dos cosas:
Si R1 y R2 son relaciones, entonces: R1 ⊂ R2 ⇒ R1n ⊂ R2n donde n es el número de composiciones de R.
S es transitiva ⇒Sn ⊂ S.
Luego
![]()
lo cual confirma que 〈R〉 es la envoltura transitiva de R.
CONCLUSIONES
Los resultados de relevancia alcanzados en este trabajo investigativo se detallan a continuación:
- Realización de las demostraciones formales y justificadas sobre la construcción de los distintos dominios numéricos sustentándose en las relaciones de equivalencia, así como en sus propiedades. Las relaciones de equivalencia y sus propiedades juegan un papel fundamental en la construcción de distintos dominios numéricos, permitiendo agrupar elementos según ciertos criterios y establecer una estructura algebraica coherente en cada conjunto de números. Estas construcciones proporcionan las bases para el desarrollo de la teoría matemática y su aplicación en diversos campos científicos y tecnológicos.
- Las ejemplificaciones brindadas tienen como propósito mostrar de modo especifico el cumplimiento de la relación según cada construcción, a su vez estas son parte inédita de esta investigación. Las ejemplificaciones ayudan a demostrar cómo las relaciones de equivalencia cumplen un papel fundamental en la formación de los números enteros, racionales, reales y complejos. Asimismo, demuestran de forma precisa cómo las relaciones de equivalencia cumplen cada una de las propiedades (reflexiva, simétrica, transitiva). Por otra parte, a partir de dichas ejemplificaciones se pueden realizar otras inferencias trascendentales que inspiren a otros investigadores a continuar obteniendo novedosos resultados.
- La construcción de los números reales mediante sucesiones de Cauchy ofrece una opción poderosa para abordar la formación de este dominio numérico, proporcionando una justificación intuitiva de la completitud de los números reales y estableciendo una conexión directa con la noción de convergencia en análisis matemático.
- La demostración detallada de las propiedades de una relación de equivalencia mediante las operaciones de unión e intersección utilizando relaciones de equivalencia y envoltura transitiva implica trabajar rigurosamente con las definiciones y propiedades fundamentales de las relaciones de equivalencia, así como con las operaciones de conjunto de unión e intersección, con el objetivo de establecer la validez de las propiedades y demostrar su aplicabilidad en diversas áreas de las matemáticas.
BIBLIOGRAFÍA
Asghari. (2005). Equivalence: An Attempt at a History of the Idea [Equivalencia: un intento de historia de la idea]. https://doi.org/https://philsci-archive.pitt.edu/14261/1/Equivalence%20An%20Attempt%20at%20a%20History%20of%20the%20Idea.pdf
Asghari, A. H. (2008). Experiencing equivalence but organizing order.
Curveira, D., & Bravo, G. (2013). Tratamiento de Conceptos Matemáticos y su repercusión en el proceso de formación profesional. Universidad y Sociedad, 10.
Gónzalez, F. (2004). Apuntes de Matemática Discreta y Relaciones de Equivalencia. Madrid: Universidad de Cadíz.
Herrera, A., & Cisneros, I. (2023). Itinerario genético de las relaciones de equivalencia en la escuela y la vida diaria. Revista Científica de FAREM - Estelí. Medio Ambiente, tecnología y desarrollo humano(45), 148–170. https://doi.org/https://doi.org/10.5377/farem.v12i45.16042
Joyce, D. (12 de Enero de 1996). Elementod de Euclide. Libro 1. Nociones Comunes. http://ficus.pntic.mec.es/~jgog0066/pitag_web/noccom.html
Kennet, R. (2004). Matmemática Discretas y sus aplicaciones. Madrid: McGRAW-HILL/Interamericana de España S. A. U.
Koulikov. (1982). Algébre et théorie des nombres. Francia: Mir.
Revilla, F. (2010). Cursos Matematicos - Relaciones de Equivalencia. https://doi.org/https://pdfcoffee.com/relaciones-de-equivalencia-4-pdf-free.html
Rojo, A. (1996). Algebra I. Buenos Aires: El Ateneo.
© 2024 Revista Científica Estelí.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
