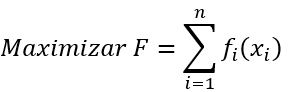https://revistas.unan.edu.ni/index.php/Multiensayo
DOI: https://doi.org/10.5377/multiensayos.v11i21.20077
Matemáticas para el futuro: soluciones sostenibles en un mundo sediento
Mathematics for the future: sustainable solutions in a thirsty world
Cliffor Jerry Herrera Castrillo
Universidad Nacional Autónoma de Nicaragua. Centro Universitario Regional de Estelí. UNAN-Managua/CUR-Estelí, Nicaragua
https://orcid.org/0000-0002-7663-2499
cliffor.herrera@unan.edu.ni
RECIBIDO
25/11/2024
ACEPTADO
01/01/2025
RESUMEN
En el presente ensayo científico se explora cómo las matemáticas juegan un papel crucial en la solución de desafíos globales, con énfasis en la gestión del agua en áreas urbanas. A través de modelos matemáticos basados en ecuaciones diferenciales y teoría de redes, se demuestra cómo las matemáticas pueden optimizar el uso del agua, reducir el desperdicio y contribuir a los Objetivos de Desarrollo Sostenible (ODS). El ensayo también destaca la importancia de la divulgación científica para inspirar a nuevas generaciones a utilizar las matemáticas para generar un impacto positivo en el mundo.
PALABRAS CLAVES
Matemáticas aplicadas; gestión del agua; sostenibilidad; ecuaciones diferenciales; ODS 6.
ABSTRACT
This scientific essay explores how mathematics plays a crucial role in solving global challenges, with emphasis on water management in urban areas. Through mathematical models based on differential equations and network theory, it demonstrates how mathematics can optimize water use, reduce waste, and contribute to the Sustainable Development Goals (SDGs). The essay also highlights the importance of science outreach to inspire new generations to use mathematics to make a positive impact on the world.
KEYWORDS
Applied mathematics; water management; sustainability; differential equations; SDG 6.
INTRODUCCIÓN
En un mundo que depende cada vez más de los avances tecnológicos y científicos, las matemáticas se presentan como una herramienta clave para abordar desafíos globales. Desde la previsión climática hasta la optimización de recursos energéticos, las matemáticas son esenciales para crear soluciones sostenibles que beneficien a las generaciones futuras. Este ensayo se centra en cómo los modelos matemáticos pueden optimizar la gestión del agua en entornos urbanos, un recurso cuya escasez es cada vez más alarmante.
Frente a los problemas ambientales, las instituciones de educación superior adquieren una importancia crucial para ayudar a reducir sus efectos y promover acciones que sensibilicen sobre las consecuencias que estos tienen en el entorno natural (Castro Martínez et al., 2024). Además, esa labor educativa y de investigación puede generar soluciones innovadoras y sostenibles que contribuyan a la preservación del medio ambiente.
Según Herrera Castrillo (2022), tanto las matemáticas como la física son consideradas grandes ciencias que han desempeñado un papel crucial en el intento de la humanidad por entender y explicar la realidad en el entorno. A lo largo de la historia, estas disciplinas han proporcionado las herramientas necesarias para analizar y modelar una amplia variedad de fenómenos que ocurren en la vida cotidiana, desde los movimientos de los cuerpos celestes hasta las interacciones en la naturaleza y los procesos tecnológicos.
Las matemáticas, en particular, ofrecen un lenguaje preciso y un marco conceptual que permite representar situaciones complejas de manera simplificada, facilitando el desarrollo de modelos que describen comportamientos y tendencias. Por otro lado, la física se centra en las leyes fundamentales que rigen el universo, permitiendo a los científicos formular teorías que explican desde la gravedad hasta la termodinámica (Herrera Castrillo, 2024).
Ambas ciencias se complementan, ya que los modelos matemáticos son fundamentales para la formulación de teorías físicas, mientras que los conceptos físicos pueden inspirar nuevas áreas de estudio en matemáticas. Esta interrelación ha permitido avances significativos en la tecnología y en la comprensión del mundo natural, subrayando la relevancia de estas disciplinas en nuestro día a día y en la búsqueda de soluciones a retos contemporáneos (Castro Cepeda et al., 2023).
El objetivo principal de este ensayo es explorar la aplicación de las ecuaciones diferenciales y la teoría de redes en la optimización del uso del agua. El análisis presentado aquí también se alinea con los Objetivos de Desarrollo Sostenible, en particular con el ODS 6: Agua limpia y saneamiento. Se pretende no solo evidenciar el valor teórico de las matemáticas en este ámbito, sino también su aplicabilidad práctica y su importancia para la sostenibilidad.
DESARROLLO
La escasez del agua como desafío global
La crisis del agua es uno de los problemas más apremiantes del siglo XXI. El crecimiento urbano desmedido, el cambio climático y la gestión ineficaz de los recursos hídricos han llevado a una disminución del acceso al agua limpia. Según la Organización de las Naciones Unidas (ONU), más de 2.200 millones de personas carecen de acceso a agua potable segura (ONU, 2021). Ante este panorama, las matemáticas se presentan como una solución prometedora para gestionar este recurso de manera más eficiente y equitativa.
El crecimiento de la población en las áreas urbanas incrementa significativamente la demanda de agua, lo que se ve agravado por la existencia de infraestructuras hídricas obsoletas o insuficientes, que generan un desperdicio considerable de este recurso vital. La falta de una planificación adecuada y de un mantenimiento sistemático contribuye a que se pierda hasta un 30% del agua en las ciudades debido a fugas en las tuberías. En este contexto, los modelos matemáticos emergen como herramientas valiosas, capaces de proporcionar soluciones precisas y efectivas para mitigar estas pérdidas (Andión Gamboa y Cárdenas Presa, 2023; García Irreño, 2023; Estévez Valencia et al., 2019).
La capacidad de los modelos matemáticos para analizar patrones de consumo de agua no solo permite identificar áreas problemáticas, sino también anticipar tendencias a largo plazo en el uso del recurso. Por ejemplo, en zonas urbanas densamente pobladas, los modelos pueden predecir el aumento de la demanda de agua en función del crecimiento demográfico y el desarrollo industrial, lo que permite a las autoridades ajustar la infraestructura antes de que ocurran crisis de escasez. Esta capacidad predictiva es esencial para garantizar un suministro continuo y eficiente, incluso ante la incertidumbre generada por fenómenos como el cambio climático.
Además, la simulación de diversos escenarios de gestión del agua proporciona una herramienta esencial para analizar el impacto de las políticas públicas antes de su implementación. Las autoridades pueden, por ejemplo, modelar las repercusiones de aumentar las tarifas del agua o de establecer restricciones de uso durante períodos de sequía (Pérez Huarachi, 2023). Al evaluar los resultados potenciales a través de simulaciones matemáticas, se pueden tomar decisiones más informadas que reduzcan el impacto en la población, al mismo tiempo que se promueve una distribución justa y responsable del recurso. Así, los modelos matemáticos se convierten en una guía para el desarrollo de políticas sostenibles y socialmente responsables.
Finalmente, la aplicación de estos modelos no solo tiene un impacto en la infraestructura y la toma de decisiones políticas, sino también en la mejora de la calidad de vida de los habitantes urbanos. Al optimizar la distribución y minimizar las pérdidas, las ciudades pueden ofrecer un acceso más equitativo al agua, lo que resulta especialmente beneficioso para las comunidades más vulnerables. En un contexto global en el que la sostenibilidad se ha convertido en una prioridad, la capacidad de las matemáticas para mejorar la gestión del agua es un claro ejemplo de cómo la ciencia puede ser una fuerza transformadora al servicio de la humanidad.
Modelos matemáticos en la gestión del agua
Un modelo matemático es un "objeto" que se utiliza como ejemplo para representarlo o, en ciertos casos, como una instancia particular que se distingue de la interpretación de esta teoría. En este sentido habitual, los diferentes conjuntos numéricos (como los números naturales, racionales y reales) son ejemplos adecuados de estructuras abstractas que carecen de contenido específico, y que pueden ser construidas o no (Herrera Castrillo, 2023).
Uno de los enfoques más eficaces para enfrentar la crisis del agua en las ciudades es la implementación de modelos matemáticos que optimicen su distribución (Roca De la Cruz, 2024). En este artículo se han empleado ecuaciones diferenciales parciales y la teoría de redes para desarrollar un modelo que busca minimizar las pérdidas de agua en las redes de distribución. A través de estos modelos, es posible identificar los puntos críticos en los sistemas urbanos donde ocurren las mayores pérdidas, lo que permite establecer estrategias de intervención específicas.
Además, estos modelos no solo sugieren mejoras en la infraestructura existente, sino que también ofrecen recomendaciones para el diseño de nuevas redes que sean más eficientes y sostenibles. Al incorporar variables como el consumo de agua, las condiciones climáticas y el estado de las infraestructuras, se puede crear un panorama más completo que ayude a los responsables de la toma de decisiones a implementar soluciones efectivas. En definitiva, la aplicación de modelos matemáticos se presenta como una herramienta valiosa no solo para reducir el desperdicio de agua, sino también para promover una gestión más inteligente y responsable de este recurso vital.
La ecuación diferencial que gobierna el flujo del agua en una tubería, como indican Delgadillo Tijerino et al. (2023) y Zeledón Herrera et al. (2024) se puede expresar como una forma simplificada de la ecuación de continuidad:
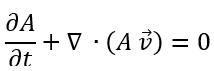 |
(1) |
Donde:
A: es el área de la sección transversal de la tubería,
![]() : es el vector velocidad del flujo de agua,
: es el vector velocidad del flujo de agua,
∇ ∙(A ![]() ): representa la tasa de cambio de flujo a través de la red.
): representa la tasa de cambio de flujo a través de la red.
Este tipo de ecuaciones modela cómo varía el flujo de agua tanto en el tiempo como en el espacio, lo que facilita la identificación de los puntos donde las pérdidas son más significativas. Al aplicar algoritmos numéricos, se pueden optimizar las soluciones de estas ecuaciones, lo que proporciona un esquema efectivo para minimizar las pérdidas y distribuir el recurso de manera más equitativa y eficiente (Cornejo Casco et al., 2023).
Por otro lado, la teoría de redes permite representar la red de distribución de agua como un grafo, donde cada nodo simboliza un punto de consumo o distribución y las aristas representan las tuberías que conectan estos puntos (German Rojas, 2023). Este enfoque permite analizar características estructurales del sistema, como la conectividad y la robustez, lo que es crucial para garantizar un suministro constante y eficiente.
La optimización de este sistema se puede realizar mediante el uso de algoritmos de flujo en redes, como el algoritmo de Ford-Fulkerson, que se centra en maximizar el flujo de agua a través de la red mientras minimiza las pérdidas que ocurren en las tuberías. Este proceso no solo mejora la eficiencia del sistema, sino que también asegura que el recurso se gestione de manera responsable y sostenible. Un ejemplo de esta optimización se puede expresar a través de una ecuación de optimización que considera variables como el caudal, la presión y la demanda en diferentes nodos de la red, permitiendo así una gestión integral y efectiva del agua (Alves Cardinot et al., 2024).
|
(2) |
Sujeto a:
|
(3) |
Donde:
F: es el flujo total optimizado en la red,
fi(Xi): es la función de flujo en la i-ésima tubería,
g(Xi): son las restricciones asociadas con las limitaciones de capacidad y distribución de la red.
Este enfoque matemático facilita la identificación de los puntos críticos en el sistema de distribución de agua, es decir, aquellos lugares donde se registran las mayores pérdidas o ineficiencias. A través de simulaciones y análisis numérico, se pueden obtener datos valiosos que permiten proponer mejoras concretas en la infraestructura existente (Dávila Quincho, 2023). Por ejemplo, al recomendar la sustitución de tuberías antiguas y desgastadas que son propensas a fugas, o la reconfiguración de la red para optimizar el recorrido del agua, reduciendo así el tiempo y la distancia que debe recorrer.
Además, este tipo de análisis permite evaluar el impacto de diferentes intervenciones antes de su implementación, asegurando que los recursos se utilicen de manera eficiente. También se pueden considerar factores como el crecimiento poblacional y el aumento de la demanda de agua, lo que ayuda a planificar futuras expansiones o mejoras en el sistema. En resumen, al aplicar un enfoque matemático riguroso, se logra no solo mejorar la eficiencia del sistema de distribución, sino también garantizar una gestión más sostenible y responsable del recurso hídrico.
Aplicación práctica de los modelos
La aplicación de modelos matemáticos en la gestión del agua no se ha limitado únicamente al ámbito teórico; se han llevado a cabo proyectos piloto en colaboración con autoridades locales, permitiendo validar su efectividad en entornos reales. En una serie de estudios de caso, se ha demostrado que la implementación de estos modelos ha logrado reducir el consumo de agua en un promedio del 20%. Este logro representa un avance considerable hacia una gestión más sostenible del recurso hídrico, al optimizar su distribución y minimizar las pérdidas debidas a fugas o ineficiencias en las infraestructuras existentes (Vegas Niño, 2023).
Además de la reducción en el consumo de agua, la implementación de estos modelos ha contribuido a la mejora de la eficiencia operativa en sistemas de distribución de agua en zonas urbanas densamente pobladas. Un ejemplo destacado es el caso de un área metropolitana, donde las fugas en las redes de distribución de agua se redujeron en más de un 15% durante el primer año de aplicación de los modelos. Esta disminución no solo se traduce en una mayor disponibilidad de agua para los residentes, sino también en una reducción significativa de los costos operativos asociados con el mantenimiento y reparación de las infraestructuras.
Los beneficios de la aplicación práctica de estos modelos van más allá de la simple mejora de la eficiencia. La optimización en la gestión del agua también ha permitido identificar zonas prioritarias para intervenciones, facilitando una planificación más estratégica en la asignación de recursos (Minango Valverde y Yturralde Parada, 2023). En entornos urbanos donde la demanda de agua es alta y las infraestructuras son antiguas, estas herramientas matemáticas permiten priorizar las áreas con mayor riesgo de fallas o fugas, asegurando una intervención más efectiva y oportuna.
Matemáticas y los Objetivos de Desarrollo Sostenible
El trabajo realizado se sitúa dentro del marco de los Objetivos de Desarrollo Sostenible (ODS), en particular en el ODS 6: Garantizar la disponibilidad de agua y su gestión sostenible para todos (Naciones Unidas, 2015). Este objetivo tiene como meta asegurar el acceso universal a agua limpia y saneamiento para 2030, y se fundamenta en soluciones innovadoras, como la optimización de recursos a través de modelos matemáticos. Las matemáticas no solo proporcionan un enfoque científico para abordar el problema del agua, sino que también actúan como herramientas para fomentar la equidad y la justicia social.
La aplicación de estos modelos matemáticos está alineada con la visión de una gestión sostenible de los recursos naturales, contribuyendo a asegurar que las futuras generaciones también tengan acceso al agua. Además, la implementación de estos modelos puede extenderse a otras áreas interrelacionadas, como la gestión de la energía o la mitigación del cambio climático, donde las matemáticas desempeñan un papel igualmente crucial. Al integrar estos enfoques, no solo se promueve una utilización más eficiente de los recursos, sino que también se avanza hacia un futuro más sostenible y justo para todos.
El Papel de la Divulgación Científica
La divulgación científica desempeña un papel fundamental en la implementación de soluciones innovadoras, especialmente en el ámbito de la gestión de recursos como el agua. Es esencial que las personas comprendan el impacto positivo que las matemáticas pueden tener en su vida diaria y en la sociedad en general. La capacidad de las matemáticas para explicar fenómenos complejos y ofrecer soluciones prácticas es un aspecto que necesita ser más visibilizado (Sánchez Fundora y Roque García, 2011).
Para generar un cambio significativo, es crucial fomentar el interés de los jóvenes en las matemáticas. Esto implica no solo motivar su curiosidad, sino también mostrarles cómo estas herramientas pueden ser utilizadas para transformar el mundo que les rodea (Nieto-Bravo et al., 2021). Las matemáticas son mucho más que simples fórmulas o problemas abstractos; son instrumentos poderosos que permiten modelar situaciones del mundo real y abordar los desafíos más apremiantes que enfrenta nuestra sociedad, como el cambio climático, la escasez de recursos hídricos y la planificación urbana sostenible.
La divulgación científica también debe enfocarse en mostrar ejemplos concretos de cómo las matemáticas se aplican en diversas áreas, desde la ingeniería hasta la economía y la biología. Al presentar historias de éxito y casos prácticos, se puede inspirar a las nuevas generaciones a ver las matemáticas como una disciplina relevante y accesible. Esto no solo ayudará a desarrollar habilidades críticas en los jóvenes, sino que también contribuirá a formar una ciudadanía más informada y capaz de participar activamente en la toma de decisiones que afectan su entorno.
CONCLUSIONES
El futuro de la gestión del agua y otros recursos esenciales dependerá en gran medida de la capacidad para aplicar soluciones matemáticas innovadoras. La crisis del agua representa solo uno de los múltiples desafíos globales en los que las matemáticas pueden tener un impacto significativo. La optimización de los sistemas de distribución de agua, usando ecuaciones diferenciales y la teoría de redes, ha demostrado ser una herramienta poderosa en la búsqueda de un acceso más equitativo y sostenible al agua. Este enfoque permite identificar y abordar ineficiencias en las redes de distribución, lo que es crucial para maximizar el uso del recurso.
Además, es fundamental continuar impulsando la investigación en este campo y fomentar el interés de las nuevas generaciones en las matemáticas aplicadas. La educación y la divulgación científica juegan un papel esencial en este proceso, ya que contribuyen a desmitificar las matemáticas y a mostrar su relevancia en la resolución de problemas reales. Al presentar ejemplos concretos de aplicaciones matemáticas en la gestión del agua, se puede incentivar a los jóvenes a ver estas disciplinas como herramientas útiles para el cambio social y ambiental.
La colaboración entre científicos, matemáticos y responsables de la toma de decisiones es otro aspecto clave para construir un futuro más sostenible. Esta sinergia permitirá desarrollar políticas informadas que integren soluciones matemáticas en la gestión de recursos, así como fomentar la creación de tecnologías innovadoras que optimicen el uso del agua y minimicen el desperdicio. Solo mediante un enfoque multidisciplinario será posible abordar de manera efectiva la crisis del agua y otros problemas críticos, asegurando que todos tengan acceso a recursos esenciales de forma justa y sostenible.
Finalmente, es importante reconocer que la gestión efectiva del agua no solo depende de la aplicación de modelos matemáticos, sino también de un compromiso generalizado hacia la sostenibilidad. Esto implica promover prácticas responsables en el consumo y la conservación del agua a todos los niveles de la sociedad. La concienciación sobre la importancia del agua como recurso limitado debe ser una prioridad, y las matemáticas pueden ser una aliada en la educación y la sensibilización sobre este tema.
Referencias bibliográficas
Alves Cardinot, D., Bastos da Silva, T., Marchon, H., & Libotte, G. (2024). Otimização do tráfego urbano utilizando o algoritmo de Ford-Fulkerson: uma abordagem para reduzir congestionamentos em cidades. Revista Interdisciplinar De Pesquisa Em Engenharia, 9(2), 91-98. https://periodicos.unb.br/index.php/ripe/article/view/52315
Andión Gamboa, M., & Cárdenas Presa, D. I. (2023). Planta docente, cambio generacional y uso de tecnologías digitales emergentes. Reencuentro. Análisis de Problemas Universitarios, 35(86), 135-152. https://reencuentro.xoc.uam.mx/index.php/reencuentro/article/view/1228
Castro Cepeda, L., Bastidas Alarcón, F., Noguera Cundar, A., & Flores Arévalo, C. (2023). Aplicación de las ecuaciones diferenciales ordinarias de primer orden para la solución de problemas físicos. Dominio de las Ciencias, 9(3), 336–355. https://doi.org/10.23857/dc.v9i3.3446
Castro Martínez, O. R., Ramírez, L. V., & Velázquez Cigarroa, E. (2024). Perspectivas de profesores sobre la educación ambiental en Nivel Medio Superior. Caso Universidad Autónoma Chapingo. EducateConCiencia, 32(4), 5-24. https://doi.org/10.58299/edutec.v32i4.794
Cornejo Casco, B. J., García López, H. D., & Herrera Castrillo, C. J. (2023). Simulador PhET para demostrar ecuación de continuidad con enfoque diferencial e integral incluyendo vectores. Revista Chilena de Educación Científica, 24(1), 14-35. http://revistas.umce.cl/index.php/RChEC/article/view/2665
Dávila Quincho, Á. D. (2023). Análisis y Propuestas de Mejora para el Impacto Vial entre las Avenidas Próceres de la independencia y 13 de enero debido a la Construcción del Centro Comercial Mall Aventura en San Juan de Lurigancho, 2023. [Tesis]. Universidad Tecnológica de Perú. https://repositorio.utp.edu.pe/handle/20.500.12867/8903
Delgadillo Tijerino, E. L., Torrez Silva, X. M., Espinoza Martínez, E. D., Medina Martínez, W. I., & Herrera Castrillo, C. J. (2023). Prototipo de trabajo práctico experimental en la demostración de la ecuación de Euler y el principio de conservación de la energía al aplicarse integrales y vectores. Revista Científica Tecnológica - RECIENTEC, 6(2), 61-73. https://revistarecientec.unan.edu.ni/index.php/recientec/article/view/212
Estévez Valencia, C., Herrera Ascencio, P., & Tiribocchi, A. (2019). Garantizar la disponibilidad de agua, su gestión sostenible y el saneamiento para todos : implementación de políticas públicas en América Latina y el Caribe. Organización de las Naciones Unidas para la Educación, la Ciencia y la Cultura (UNESCO), Conferencia de Directores Iberoamericanos de Aguas (CODIA). https://bvearmb.do/handle/123456789/4675
García Irreño, Y. (2023). Identificación de pérdidas de agua durante el proceso de potabilización en la planta de tratamiento agua potable operada por la Empresa de Servicios Públicos de Acueducto, Alcantarillado y Aseo del Líbano Tolima - EMSER E.S.P. [Informe Final de Pasantía]. Universidad Distrital Francisco José de Caldas. https://repository.udistrital.edu.co/items/7c1ff747-c965-4f4b-8911-1d4d27b20c81
German Rojas, C. A. (2023). Desarrollo de métodos automáticos de simplificación de redes de distribución de agua mediante el uso de la teoría de grafos. [Trabajo Fin de Máster]. Universitat Politècnica de València. https://riunet.upv.es/handle/10251/198909
Herrera Castrillo, C. J. (2022). Aprendizaje de ecuaciones diferenciales aplicadas en física utilizando tecnología. Revista Torreón Universitario, 7(31), 26–35. https://doi.org/10.5377/rtu.v11i31.14223
Herrera Castrillo, C. J. (2023). Interdisciplinariedad a través de la Investigación en Matemática y Física. Revista Chilena de Educación Matemática, 15(1), 31-45. https://doi.org/10.46219/rechiem.v15i1.126
Herrera Castrillo, C. J. (2024). Ecuaciones en fenómenos físicos. Logos Boletín Científico de la Escuela Preparatoria No. 2, 11(22), 15-19. https://doi.org/10.29057/prepa2.v11i22.12323
Minango Valverde, L. M., & Yturralde Parada, P. N. (2023). Análisis de zonas con alta demanda hídrica en la ciudad de Guayaquil utilizando sistemas de información geográfica SIG. [Tesis de Grado]. Universidad Laica Vicente RocaFuerte. http://repositorio.ulvr.edu.ec/handle/44000/6644
Naciones Unidas. (2015). Objetivos de Desarrollo Sostenible. https://www.un.org/sustainabledevelopment/es/objetivos-de-desarrollo-sostenible/
Nieto-Bravo, J. A., Pérez-Vargas, J. J., & Santamaría-Rodríguez, J. E. (2021). Desafíos a la divulgación científica del conocimiento en la actualidad. Civilizar Ciencias Sociales y Humanas, 21(40), 9-10. Obtenido de http://www.scielo.org.co/scielo.php?pid=S1657-89532021000100009&script=sci_arttext
Organización de las Naciones Unidas [ONU]. (2021). Informe mundial sobre el desarrollo de los recursos hídricos: Valorando el agua. UNESCO. https://unesdoc.unesco.org/ark:/48223/pf0000375724
Pérez Huarachi, R. B. (2023). Modelación y gestión de recurso hídrico del sistema de Achachicala considerando escenarios de cambio climático con aplicación WEAP. [Tesis de Grado]. Universidad Mayor de San Andrés. https://repositorio.umsa.bo/handle/123456789/34357
Roca De la Cruz, M. P. (2024). Mejora del balance hídrico mediante la implementación de técnicas de optimización fundamentadas en bases de datos hidráulicas en la presa Cuchoquesera provincia de Cangallo, departamento de Ayacucho, 2023. [Tesis]. Universidad Nacional de San Cristóbal de Huamanga. https://repositorio.unsch.edu.pe/items/bb73b6af-2580-405e-aae9-b4caea2b6736
Sánchez Fundora, Y., & Roque García, Y. (2011). La divulgación científica: una herramienta eficaz en centros de investigación. Revista. Bibliotecas. Anales de investigación, 7(7), 91-94. http://revistas.bnjm.sld.cu/index.php/BAI/article/view/315/323
Vegas Niño, Ó. T. (2023). Nuevas herramientas para la gestión técnica de redes de distribución de agua basadas en el modelo matemático y la topología de la red. [Tesis Doctoral]. Universitat Politècnica de València. https://riunet.upv.es/handle/10251/192474
Zeledón Herrera, G. J., Pérez Aguilar, K. A., Laguna Laguna, Y. J., & Herrera-Castrillo, C. J. (2024). Conectando Puntos: Un Prototipo de Trabajo Práctico para Explorar la Ecuación de Continuidad. Revista Científica Ciencia Y Tecnología, 24(43). https://doi.org/10.47189/rcct.v24i43.673
© 2025 Revista Multi-Ensayos.
![]() Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.
Este trabajo está licenciado bajo una Licencia Internacional Creative Commons 4.0 Atribución-NoComercial-CompartirIgual.