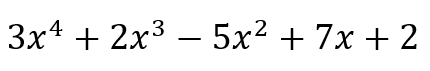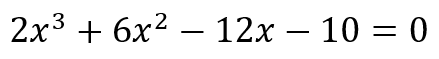Retos y desafíos en el aprendizaje del álgebra polinomial y lineal en la carrera de Matemáticas

 

Cliffor Jerry Herrera Castrillo
Universidad Nacional Autónoma de Nicaragua, Managua UNAN-Managua. Centro Universitario Regional de Estelí. UNAN-Managua-CUR-Estelí, Nicaragua.
https://orcid.org/0000-0002-7663-2499
cliffor.herrera@unan.edu.ni

Oliver Santiago López
Universidad Nacional Autónoma de Nicaragua, Managua UNAN-Managua. Centro Universitario Regional de Estelí. UNAN-Managua-CUR-Estelí, Nicaragua.
https://orcid.org/0000-0002-4469-920X
oliverlp87@gmail.com

RECIBIDO

15/10/2024

ACEPTADO

14/01/2025

 

 

INTRODUCCIÓN

 

Para Osorio Vidal et al. (2023) existe la necesidad del aprendizaje del álgebra, ya que la enseñanza de componentes o asignaturas, relacionados a la parte abstracta de las matemáticas exige ciertas particularidades, donde los docentes al hacer uso de la creatividad e innovación, deben motivar a los estudiantes a interesarse por el álgebra polinomial y lineal, demostrándoles que los aprendizajes adquiridos serán útiles en el ejercicio profesional; en tal sentido los docentes deben articular los contenidos curriculares necesarios del curso con el empleo de la tecnología, para hacer más amigables las clases.

Dorier (2016) reconoce que el aprendizaje del Álgebra resulta difícil y complejo para la mayoría de los estudiantes universitarios, esto por ser una disciplina demandante desde el punto de vista cognitivo, que requiere que el estudiante sea capaz de moverse entre diferentes lenguajes (teoría de matrices y teoría de los espacios vectoriales), puntos de vista cartesiano y paramétrico, y registros semióticos. (Dorier y Sierpinska, 2001).

En la carrera de Matemáticas, se espera que los estudiantes sean capaces de comprender y desarrollar demostraciones matemáticas rigurosas. Sin embargo, la construcción de demostraciones en álgebra polinomial y lineal puede resultar especialmente desafiante debido a la complejidad de las estructuras algebraicas involucradas. Por ello es necesaria una introducción gradual a la lógica y la estructura de las demostraciones, dando paso a ejercicios y problemas que permitan a los estudiantes practicar la construcción de argumentos matemáticos sólidos. Como indican León Loaiza M. y León Loaiza L. (2023):

En este ensayo, se exploran diversas estrategias pedagógicas implementadas con veinticinco estudiantes, doce de II año y trece de IV año de la Carrera de Matemáticas del CUR-Estelí de la UNAN-Managua, durante el primer semestre 2023, para así dar pautas a fin de superar los desafíos del álgebra polinomial y lineal. Se destaca la importancia de establecer conexiones entre los conceptos matemáticos y la vida cotidiana, utilizando ejemplos concretos y contextualizados para facilitar la comprensión. Además, se discute la importancia de una enseñanza gradual y progresiva, brindando a los estudiantes una base sólida en álgebra básica antes de abordar temas más avanzados.

Por consiguiente esta enseñanza gradual y progresiva se ve reflejada desde educación media en donde se introducen conceptos de variables y coeficientes, conforme se avanza en su formación básica el estudiante aprende las operaciones básicas y simples de expresiones algebraicas, casos de factorización, ecuaciones y desigualdades así como también sus diferentes gráficos y raíces, fortaleciendo esta base en el álgebra polinomial con conceptos y operaciones que involucran variables elevadas a diferentes potencias y coeficientes, así como las raíces o soluciones a polinomios utilizando como base de números reales y complejos.

Asimismo, se busca examinar la importancia de la práctica activa y la resolución de problemas como una estrategia efectiva para fortalecer las habilidades en el álgebra polinomial y lineal. A través de la resolución de una variedad de problemas, los estudiantes aplican los conceptos aprendidos y desarrollan sus capacidades para enfrentar desafíos matemáticos de manera independiente.

Además, se explora el papel de los recursos tecnológicos en el aprendizaje del álgebra polinomial y lineal. Recursos como CoCoA¹ , GeoGebra² , Khan Academy³ , Wolfram Alpha⁴ , Desmos⁵ , MATLAB⁶ , Wordwall⁷ y Google forms⁸ que ofrecen herramientas interactivas, tutoriales y ejercicios que permiten a los estudiantes visualizar conceptos abstractos, resolver ecuaciones, aprender jugando y explorar relaciones algebraicas de manera más accesible y atractiva.

Es importante, tomar en cuenta que según los estudios de Báez et al. (2017), Martín y Pérez (2019) y Pérez González (2020) el Cálculo Diferencial y el Álgebra Lineal constituyen las asignaturas con mayores dificultades didácticas, esto por el rigor requerido en la formación y desarrollo conceptual, por ser una de las materias que más reciben los estudiantes de la carrera de Matemáticas en su formación, como indican Martínez Suárez y Romero Díaz (2019):

La razón detrás de lo mencionado anteriormente radica en que a niveles avanzados las clases de álgebra se ven impregnadas por la tendencia a traducir de lenguaje común a lenguaje algebraico las demostraciones rigurosas. Esto plantea un desafío significativo para los educadores, quienes deben abordar la enseñanza de manera tanto didáctica como científica, por consiguiente, el objetivo es “reforzar la capacidad creativa en el ejercicio de la profesión docente mediante propuestas didácticas innovadoras como soluciones a los problemas inherentes al proceso de enseñanza aprendizaje del álgebra” (UNAN-Managua, 2021, p. 99).

A continuación, en la figura 1, se muestra la secuencia lógica del eje de Álgebra que siguen los estudiantes de la carrera de Matemáticas.

Figura 1 Componentes del Eje de álgebra de la Carrera de Matemáticas

Nota. Adaptado de (UNAN-Managua, 2021, p. 99) y (Parrilla Rivera et al., 2016, p. 4)

Al destacar los componentes de interés de este ensayo, se pude deducir:

Figura 2 Descripción de los componentes de Álgebra Polinomial y Álgebra Lineal

Nota. Adaptado de (UNAN-Managua, 2021, p. 99) y (Parrilla Rivera et al., 2016, p. 4)

En el mundo de las matemáticas, el álgebra polinomial y lineal desempeña un papel fundamental. Desde la resolución de ecuaciones hasta el análisis de relaciones entre variables, el estudio del álgebra proporciona las herramientas necesarias para comprender y modelar una amplia variedad de fenómenos. Sin embargo, muchos estudiantes se enfrentan a desafíos al aprender y dominar estos conceptos.

El componente de algebra polinomial se planifica con un enfoque por competencias. Según UNAN-Managua (2021), los componentes del eje Álgebra se basan en la actividad cognoscitiva del estudiante durante el proceso de enseñanza-aprendizaje y pretende mejorar el proceso de instrucción y calidad educativa a través de las etapas de orientación, ejecución y control de la actividad. (p. 107)

Esto indica que el componente de algebra polinomial al pertenecer a este eje vertical en la carrera de matemática tiene como propósito central la actividad cognitiva del estudiante, mejorar la instrucción y por ende la calidad de su aprendizaje, logrando un conocimiento básico de la teoría de polinomios, especialmente en el manejo de estructuras algebraicas y aplicación usando como guía de este proceso las bases orientadoras de la acción (BOA), que el facilitador garantiza a los estudiantes.

Según la UNAN- Managua (2016), la asignatura de algebra lineal se planifica con un enfoque por objetivos conceptuales, procedimentales y actitudinales con el fin de ampliar los conocimientos de los estudiantes, demostrar propiedades matemáticas y fomentar una actitud positiva en situaciones cotidianas, como el beneficio de una comprensión más profunda del algebra, la capacidad de demostrar una situación con una propiedad matemática y dar su significado, tomando en cuenta las actitudes positivas hacia los conceptos de algebra lineal que ayuden al estudiante a resolver problemas del mundo real.

DESARROLLO

En el mundo de las matemáticas, el álgebra polinomial y lineal desempeña un papel fundamental. Desde la resolución de ecuaciones hasta el análisis de relaciones entre variables, el álgebra proporciona las herramientas necesarias para comprender y modelar una amplia variedad de fenómenos. Sin embargo, muchos estudiantes se enfrentan a desafíos al aprender y dominar estos conceptos.

El álgebra polinomial y lineal se caracterizan por su naturaleza abstracta y simbólica. Los estudiantes a menudo luchan para comprender y visualizar conceptos abstractos como variables, coeficientes y ecuaciones. La falta de una comprensión sólida de estos conceptos dificulta la resolución de problemas y el razonamiento algebraico. Los profesores deben enfocarse en proporcionar ejemplos concretos, utilizar representaciones gráficas y fomentar la práctica constante para ayudar a los estudiantes a desarrollar una comprensión intuitiva de los conceptos abstractos. Como indica Barreto García, (2023) “… la actividad fundamental en las clases de Matemática sea el razonamiento que efectúen nuestros estudiantes, la enseñanza será tanto más activa cuanto más haga funcionar la imaginación” (p. 18).

El algebra polinomial resulta desafiante para muchos estudiantes, quienes a menudo no encuentran la conexión con el mundo real, para tal dificultad los docentes tienden a incorporar estrategias y procesos pedagógicos que fomenten una comprensión más profunda y significativa de estos conceptos, como la utilización de ejemplos concretos que conecten que conecten la teoría abstracta con situaciones prácticas, por ejemplo, al explicar el concepto de ecuaciones lineales, los profesores pueden recurrir a problemas del mundo real, como el cálculo de costos en la compra de varios artículos, lo que ayuda a los estudiantes a visualizar la aplicabilidad de las ecuaciones lineales en contextos cotidianos.

Para continuar con el desarrollo de este ensayo, resulta pertinente establecer las diferencias entre desafío y reto que son dos términos frecuentemente utilizados para describir situaciones que implican dificultad o superación. Aunque a menudo se usan indistintamente, hay una sutil diferencia entre ambos conceptos.

Un desafío se refiere a una situación que presenta obstáculos o dificultades, generalmente percibidos como negativos, que requieren esfuerzo y habilidad para superar. En el contexto del álgebra polinomial y lineal, los desafíos pueden manifestarse en la comprensión de conceptos abstractos, la resolución de ecuaciones complicadas o la aplicación de fórmulas en situaciones problemáticas.
Por otro lado, un reto se refiere a una situación que estimula y motiva al individuo a superar un objetivo o alcanzar un logro. Los retos son vistos como oportunidades para crecer, aprender y demostrar habilidades. En el ámbito del álgebra polinomial y lineal, los retos pueden manifestarse en la resolución de problemas más complejos o en la aplicación de los conceptos aprendidos en situaciones novedosas.

Los retos y desafíos, en los cuales se estará profundizando y ejemplificando en este ensayo se muestran en la figura 3:

Figura 3
Retos y desafíos del Álgebra Polinomial y Lineal

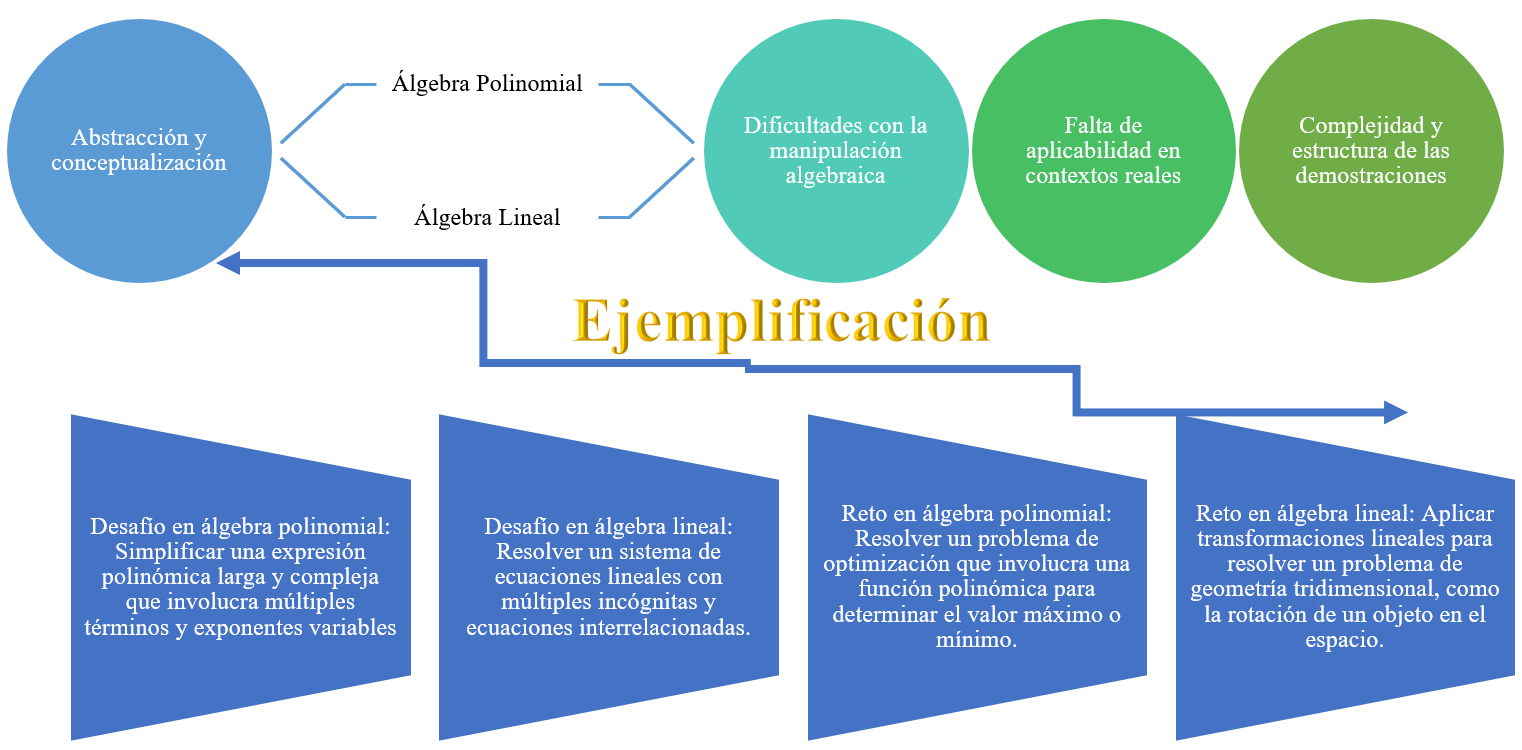
Nota. Elaboración Propia

En la figura 3 se muestran los principales retos y desafíos a los que se enfrentan los estudiantes de matemáticas y además un ejemplo de retos y desafíos en álgebra polinomial y lineal un desafío común en el álgebra polinomial es la simplificación de expresiones polinómicas largas y complejas. Por ejemplo, si se considera la expresión polinómica:

(1)

El desafío aquí radica en simplificar la expresión y reducirla a su forma más simple. Los estudiantes deben aplicar las propiedades de los exponentes y combinar términos semejantes para simplificar la expresión. Para superar este desafío, es importante que los estudiantes comprendan los conceptos de exponentes, términos semejantes y las reglas básicas de operaciones en álgebra polinomial.

(1)

 Por otro lado, en el álgebra lineal, un reto común es la resolución de sistemas de ecuaciones lineales. Por ejemplo, al considerar el siguiente sistema de ecuaciones:

(2)

Resolver este sistema implica encontrar los valores de  e  que satisfacen ambas ecuaciones simultáneamente. Los estudiantes deben aplicar métodos como la eliminación, sustitución o la matriz ampliada para resolver el sistema. Este reto requiere habilidades de manipulación algebraica, comprensión de las propiedades de las operaciones lineales y la capacidad de trabajar con ecuaciones simultáneas.

En el caso, de los retos, como se mencionó anteriormente son oportunidades, para crecer, mejorar y aprender, en el algebra polinomial, un ejemplo básico es describir las técnicas de resolución de ecuaciones polinomiales y los métodos principales de acotación, separación y aproximación de las raíces reales de un polinomio entero, racional, real o complejo, esto utilizando el método de Cardano⁹ , en la ecuación.

(3)

El reto, está en que el estudiante, debe dominar un sinnúmero de ecuaciones y seguir un proceso extenso, para lograr encontrar las raíces deseadas, tomando en cuenta que es una ecuación cúbica de la forma . Dentro de las ecuaciones se encuentran.
Para encontrar variables  y  

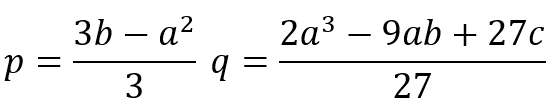(4)

Para encontrar la variación de la ecuación:

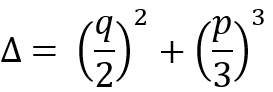(5)

Y, por último, para encontrar las raíces de la ecuación:

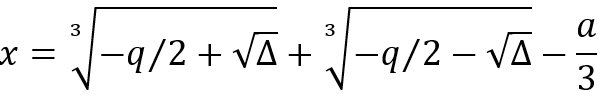(6)

Llegar a resolver este tipo de ejercicios, requiere de amplios conocimientos algebraicos básicos y el manejo de exponentes y radicales correctamente.
Por otro lado, en el álgebra lineal, puede ser considerado un reto comprender y hacer uso correcto del teorema de Carathedory⁹ . Por ejemplo, sean:

(7)

Compruebe que

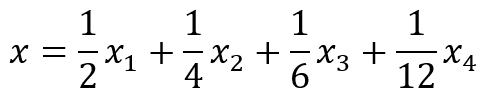(8)

Utilizar el teorema de Carathedory para expresar  como combinación lineal convexa de solamente  vectores de  (Hacerlo para . Este tipo de problemas representa un reto, ya que se deben manejar varias operaciones algebraicas, así como espacios vectoriales y convexos, solucionar sistema de ecuaciones con  incógnitas y realizar operaciones con vectores y escales.

Además de estos ejemplos, existen otros retos y desafíos en el álgebra polinomial y lineal, como la comprensión de conceptos abstractos, los espacios vectoriales, la diagonalización de matrices o la aplicación de teoremas clave como el teorema del valor medio. Estos desafíos pueden presentar dificultades adicionales para los estudiantes, ya que requieren un nivel más avanzado de abstracción y razonamiento matemático.

Los retos y desafíos en el álgebra polinomial y lineal abarcan diversos aspectos, como la abstracción y conceptualización algebraica, la manipulación algebraica, la aplicabilidad del álgebra y la complejidad en las demostraciones. A continuación, se describirán y analizarán cada uno de estos desafíos y cómo pueden afectar el aprendizaje y dominio del álgebra.

Abstracción y conceptualización algebraica

Para Rendón y Hoyos (2016) en el proceso de enseñanza-aprendizaje del álgebra, al mencionar lenguaje o notación matemática, se tratan de aspectos de conceptualización, muy relacionados con la comprensión y abstracción algebraica, que dan acceso al aprendizaje conceptual de un objeto matemático, mediante su manipulación y transformación de su representación semiótica. “Algebrizar la matemática elemental es capacitar a los estudiantes mediante el fomento de un mayor grado de generalidad en su pensamiento y una mayor capacidad de comunicar dicha generalidad” (Lins y Kaput, 2004, p. 58).

La abstracción es un desafío común en el álgebra, ya que implica la capacidad de comprender y trabajar con conceptos abstractos que no están vinculados directamente con objetos físicos. Por ejemplo, en el álgebra polinomial, los estudiantes deben comprender que un polinomio es una expresión algebraica compuesta por términos con coeficientes, exponentes y variables. Esto requiere un pensamiento abstracto y la capacidad de generalizar patrones y reglas.

La conceptualización algebraica implica la capacidad de comprender y aplicar los conceptos fundamentales del álgebra. Los estudiantes deben comprender conceptos como variables, ecuaciones, sistemas de ecuaciones y funciones, así como las relaciones entre ellos. Esta conceptualización sólida es esencial para abordar problemas más complejos y aplicar el álgebra en diferentes contextos.

Un ejemplo práctico, es al ver la aplicación en el área de Física, al Imaginar que se está planeando un viaje por carretera y se quiere calcular cuánto tiempo tomará llegar a un  destino. Se puede usar la fórmula de distancia igual a velocidad por tiempo  para determinar el tiempo necesario. Aquí, la variable “” representa la distancia, “” representa la velocidad y “” representa el tiempo. La abstracción y conceptualización algebraica implicaría comprender que esta fórmula se puede aplicar en diferentes situaciones de viaje y utilizarla para calcular el tiempo requerido en cada caso específico.

Manipulación algebraica

La manipulación algebraica es otro desafío importante en el álgebra. Implica la capacidad de realizar operaciones algebraicas como simplificar expresiones, resolver ecuaciones, factorizar polinomios y realizar operaciones con matrices. La manipulación algebraica requiere habilidades de cálculo, conocimiento de las propiedades y reglas algebraicas, y la capacidad de seguir pasos lógicos para llegar a una solución.

Para Aké Tec y Larios Osorio (2020) la manipulación algebraica se encuentra despojada de significado a través de reglas y procedimientos sintácticos. Se llega a pensar que el uso de las letras (variable) es una condición necesaria para el pensamiento algebraico, pues el reconocimiento de lo general es un requerimiento previo para denotar el simbolismo; además, existe la posibilidad de manipulación simbólica sin sentido. (Zazkis y Liljedahl, 2002)

La manipulación algebraica puede volverse especialmente compleja cuando se trabaja con expresiones polinómicas o sistemas de ecuaciones lineales con múltiples variables e incógnitas. Los estudiantes deben aprender a organizar y manipular términos, aplicar propiedades algebraicas y utilizar estrategias adecuadas para simplificar y resolver problemas.

Se puede, decir que un ejemplo práctico y sencillo, sería al tener la expresión algebraica . El desafío aquí es simplificar y combinar los términos semejantes para obtener una forma más simple de la expresión. Al combinar los términos con , se obtendría

Aplicabilidad del álgebra

Un desafío común para los estudiantes es comprender la aplicabilidad del álgebra en situaciones del mundo real. A menudo, los estudiantes pueden tener dificultades para relacionar los conceptos abstractos del álgebra con situaciones prácticas y problemas del mundo real. Es importante que los profesores proporcionen ejemplos y aplicaciones concretas para ayudar a los estudiantes a ver cómo el álgebra se aplica en campos como la física, la economía, la ingeniería y la estadística.

Por ejemplo, en la economía, se puede aplicar el álgebra para comprender y resolver problemas relacionados con las finanzas. Se pueden utilizar ecuaciones lineales para modelar y resolver problemas de presupuesto, cálculo de intereses o análisis de ingresos y gastos. También se pueden mencionar otras aplicaciones, como las que se muestran en la figura 4:

Figura 4

Aplicaciones del Álgebra Polinomial en diferentes áreas

Nota. Elaboración propia, a partir de experiencia de los autores

Estos son solo algunos ejemplos de cómo el álgebra polinomial tiene aplicaciones en la vida cotidiana. En general, el álgebra polinomial es una herramienta matemática poderosa que se utiliza en una amplia gama de campos y disciplinas para modelar, analizar y resolver problemas del mundo real. Ahora se presentan aplicaciones del Álgebra Lineal:

Figura 5

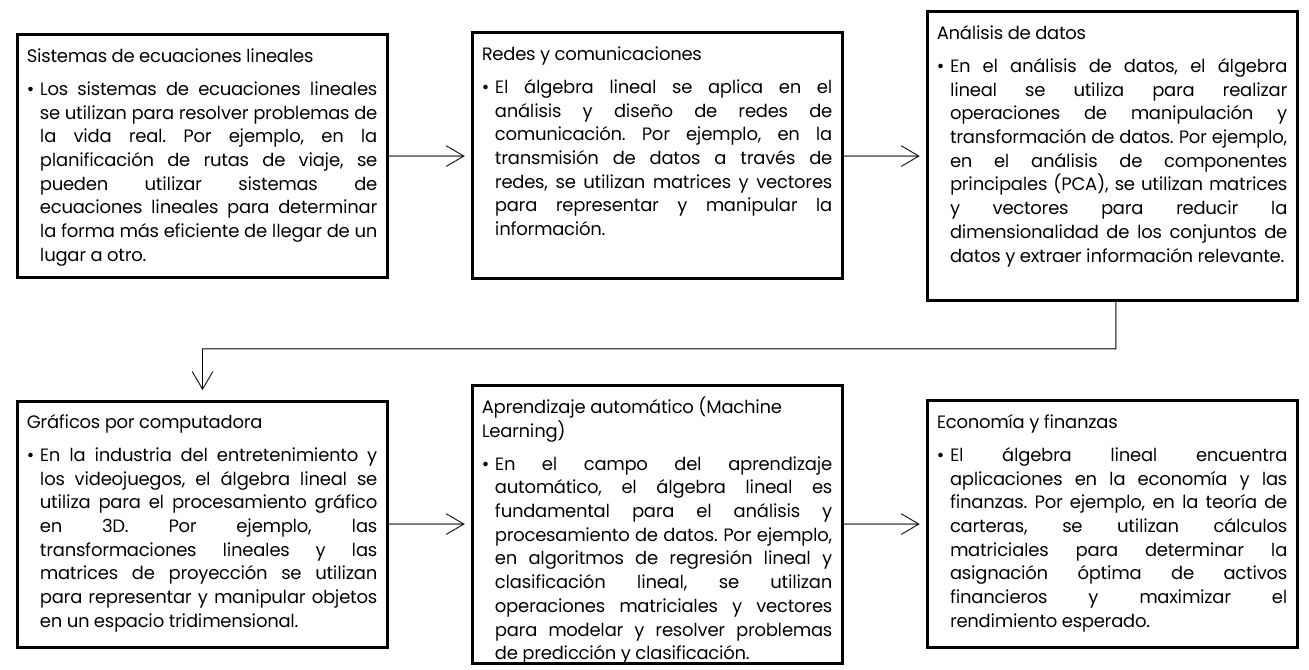
Aplicaciones del Álgebra Lineal en diferentes áreas

Nota. Elaboración propia, a partir de experiencia de los autores

Estos son solo algunos ejemplos de cómo el álgebra lineal tiene aplicaciones en la vida cotidiana. En general, el álgebra lineal es una herramienta matemática esencial en numerosos campos, desde la ciencia y la ingeniería hasta la economía y la tecnología, que permite modelar y resolver problemas del mundo real de manera efectiva.

Complejidad en las demostraciones

La demostración de teoremas y propiedades algebraicas puede representar un desafío significativo para los estudiantes. Las demostraciones requieren un razonamiento lógico, la comprensión profunda de los conceptos algebraicos y la capacidad de seguir una secuencia lógica de pasos para llegar a una conclusión válida. Las demostraciones pueden ser especialmente complejas en álgebra lineal, donde se abordan temas como la diagonalización de matrices o la independencia lineal.

Según Fadil y Puig (2014) para lograr hacer una demostración, los estudiantes deben conocer la naturaleza y los rasgos de las propias demostraciones, para sus procesos de solución. En ocasiones es necesaria la manipulación de figuras geométricas, aunque algebraicamente la mayoría de las demostraciones están hechas en un lenguaje retórico, es decir con ausencia del lenguaje simbólico, esto no impide calificarlas de algebraicas porque los conceptos que las nutren son algebraicos y no apelan explícitamente a las proposiciones de Euclides, siendo importante realizar un proceso de enseñanza basado en la explicación de los conceptos usando ejemplos.

Para superar estos retos y desafíos en el álgebra polinomial y lineal, es fundamental contar con estrategias pedagógicas efectivas. Los profesores pueden utilizar enfoques graduales, proporcionar ejemplos concretos, aplicaciones prácticas, y fomentar la resolución activa de problemas. Además, el uso de recursos tecnológicos, como software de álgebra interactiva o herramientas de visualización, pueden ayudar a los estudiantes a comprender conceptos abstractos y abordar problemas de manera más eficiente.

En álgebra lineal, un ejemplo de complejidad en las demostraciones es el teorema de la matriz inversa. Este teorema establece que, si una matriz  es invertible, entonces su matriz inversa  existe. Demostrar este teorema implica realizar una serie de pasos lógicos, como demostrar que la matriz inversa es única y que la matriz original multiplicada por su inversa da como resultado la matriz identidad.

Soluciones pedagógicas para superar los desafíos

Para abordar los desafíos mencionados en el álgebra polinomial y lineal, es importante implementar soluciones pedagógicas efectivas. Aquí hay algunas estrategias que los educadores utilizaron para ayudar a los estudiantes a superar estos desafíos:

Figura 6
Soluciones pedagógicas que ayudan a superar desafíos algebraicos

Nota. Elaboración Propia

Enfoque gradual

Comenzar con conceptos y problemas más simples y progresar hacia niveles de dificultad más altos. Esto permite a los estudiantes construir una base sólida y desarrollar gradualmente habilidades más avanzadas. Por ejemplo, en lugar de introducir de inmediato expresiones polinómicas complejas, se pueden comenzar con expresiones más simples y luego aumentar gradualmente la complejidad a medida que los estudiantes adquieran confianza y comprensión.

Con los estudiantes de II y IV año de la Carrera de Matemáticas, se utilizó el enfoque gradual, iniciando en el Álgebra Polinomial, donde los estudiantes, para encontrar raíces reales y complejas de cualquier polinomio de n grado, recordaron los casos de factorización, productos notables y operaciones con polinomios a través de diferentes juegos didácticos. Es importante mencionar que para esto se tomó como base los libros de texto del Ministerio de Educación (MINED) de Nicaragua, que es el cocimiento previo que traen los estudiantes universitarios.

Figura 7
Estudiantes de II año de Matemáticas repasando operaciones con polinomios

Nota. Fotografías tomadas por los autores

Las operaciones con polinomios, como la suma, resta, multiplicación y división de polinomios son conceptos básicos en Álgebra. Al aprender a utilizar estas operaciones, los estudiantes adquieren habilidades fundamentales que les permiten resolver problemas más complejos y aplicar estos conceptos en otras áreas de las matemáticas y la vida cotidiana.

Además, el estudio de las operaciones con polinomio al igual que la factorización y productos notables, permiten a los estudiantes familiarizarse con la notación algebraica y desarrollar habilidades de manipulación algebraica, que son fundamentales en álgebra y en áreas relacionadas como cálculo y geometría.

Ejemplos concretos y aplicaciones prácticas

Proporcionar ejemplos concretos y aplicaciones prácticas del álgebra para ayudar a los estudiantes a relacionar los conceptos abstractos con situaciones de la vida real. Estos ejemplos pueden incluir problemas relacionados con la física, la economía, la ingeniería u otras disciplinas. Al mostrar cómo se aplica el álgebra en contextos reales, los estudiantes pueden comprender mejor la utilidad y relevancia de los conceptos algebraicos.

En IV año de Matemáticas, en la Unidad 7 Aplicaciones: Polinomios de Bernstein. Curvas de Bézier. Algoritmo de Casteljau. Derivadas. Parametrización singular. Un algoritmo tetraédrico. Integración. Conversión a la representación de Bézier. Conversión a la forma monomial, fue posible visualizar con los estudiantes la manera en que se utilizan todos los conceptos algebraicos en la vida cotidiana, para ello se crearon organizadores gráficos de manera creativa.

Figura 8
Exposición de organizadores gráficos sobre aplicaciones de conceptos algebraicos por estudiantes de IV año de Matemáticas

Nota. Fotografías tomadas por los autores

Uso de recursos tecnológicos

Utilizar herramientas y recursos tecnológicos, como software de álgebra interactiva, calculadoras gráficas o aplicaciones móviles, puede ayudar a los estudiantes a visualizar y experimentar con conceptos algebraicos. Estas herramientas pueden facilitar la comprensión de las propiedades algebraicas, la manipulación de expresiones y la resolución de problemas. Además, pueden proporcionar retroalimentación inmediata y guiar a los estudiantes a través de pasos lógicos en la resolución de problemas.

Los programas como CoCoA, Khan Academy, Wolfram Alpha, Desmos y MATLAB desempeñan un papel crucial en la resolución de desafíos en álgebra lineal y polinomial. Estas herramientas proporcionan recursos valiosos, funcionalidades y capacidades computacionales que permiten a los usuarios abordar problemas complejos y explorar conceptos en estas áreas de las matemáticas.

CoCoA es un sistema de álgebra computacional especializado en álgebra conmutativa y geometría algebraica. Su funcionalidad avanzada y amplia gama de herramientas permiten a los usuarios trabajar con polinomios, ideales y variedades algebraicas. CoCoA es especialmente útil para resolver problemas en álgebra polinomial y conmutativa de manera eficiente, lo que incluye simplificar expresiones, factorizar polinomios, calcular bases de Gröbner y resolver sistemas de ecuaciones polinomiales (Abbott y Bigatti, 2014). Su capacidad para realizar cálculos simbólicos y numéricos lo convierte en una herramienta esencial para investigadores y profesionales en matemáticas y ciencias relacionadas.

Además, CoCoA ofrece una interfaz de línea de comandos y una interfaz gráfica de usuario, lo que facilita su uso y lo hace accesible para usuarios con diferentes niveles de experiencia en programación y matemáticas. Este sistema se utilizó con estudiantes de IV año de Matemáticas, para trabajar la Unidad 3: El álgebra de Matrices y Determinantes. Operaciones con matrices. Propiedades. Matrices invertibles. Matrices elementales. Cálculo de la matriz inversa. Permutaciones. Determinantes de una matriz cuadrada. Propiedades de los determinantes. Menores y complementos algebraicos. Definición de determinantes. Propiedades. Matriz adjunta y regla de Cramer. Cofactor. Matriz de cofactores. Adjunta de una matriz.

Por otro lado, también se hizo uso efectivo de Khan Academy que es una plataforma en línea que ofrece una amplia variedad de recursos educativos, incluyendo lecciones y ejercicios interactivos en álgebra lineal y polinomial. Proporciona una base sólida para los estudiantes de II y IV año de Matemáticas, cubriendo temas desde conceptos básicos hasta temas más avanzados. Khan Academy utiliza un enfoque paso a paso y brinda explicaciones claras, lo que facilita la comprensión de los conceptos y la resolución de problemas. Los estudiantes lograron practicar sus habilidades a través de ejercicios interactivos y recibir retroalimentación inmediata. Khan Academy es una herramienta invaluable para el aprendizaje autodidacta y el desarrollo de habilidades en álgebra lineal y polinomial.

Para la resolución de ejercicios, fue práctico el uso de Wolfram Alpha que es un motor de conocimiento computacional que puede realizar cálculos matemáticos avanzados y proporcionar respuestas y soluciones paso a paso. En álgebra lineal y polinomial, Wolfram Alpha es útil para realizar operaciones básicas, resolver sistemas de ecuaciones lineales, encontrar raíces y factores de polinomios, calcular determinantes y realizar transformaciones lineales, entre otros. Su capacidad para mostrar pasos intermedios y proporcionar visualizaciones gráficas ayuda a los usuarios a comprender los procesos y conceptos detrás de los cálculos. Wolfram Alpha es una herramienta poderosa para estudiantes, profesionales y entusiastas de las matemáticas que necesitan respuestas rápidas y precisas en álgebra lineal y polinomial.

También, el uso de Desmos la calculadora gráfica en línea permitió trazar gráficos de funciones, explorar relaciones matemáticas y resolver ecuaciones. Es especialmente en álgebra polinomial y lineal, ya que permitió visualizar gráficamente polinomios, sistemas de ecuaciones lineales y otras funciones matemáticas. Desmos también ofrece una interfaz interactiva donde los usuarios pueden manipular gráficos y observar cómo los cambios en los parámetros afectan a las funciones. Esta herramienta es valiosa para la comprensión visual y la experimentación en álgebra lineal y polinomial.

Tanto Wordwall como Google Forms son herramientas de enseñanza útiles para el álgebra polinomial y lineal. Wordwall permite a los educadores crear actividades interactivas como crucigramas y juegos de correspondencia, lo que ayuda a los estudiantes a familiarizarse con la terminología y a practicar la traducción entre diferentes representaciones algebraicas. Por otro lado, Google Forms facilita la creación de cuestionarios y formularios personalizados, lo que permite evaluar el conocimiento de los estudiantes, recopilar datos y proporcionar retroalimentación (Cevallos Santacruz, 2021). Ambas herramientas son versátiles y se adaptan a las necesidades de los educadores y estudiantes, mejorando así el aprendizaje de álgebra polinomial y lineal.
Ejemplos de uso de Wordwall:

• Crucigrama de términos algebraicos: Un educador crea un crucigrama en Wordwall con términos clave como "monomio", "polinomio", "ecuación lineal", etc. Los estudiantes deben completar el crucigrama, lo que les ayuda a familiarizarse con la terminología y fortalecer su comprensión de los conceptos.
• Juego de correspondencia de expresiones y gráficas: Se crea un juego en Wordwall donde los estudiantes deben relacionar expresiones algebraicas con sus correspondientes gráficas. Esto ayuda a los estudiantes a comprender la relación entre las expresiones y sus representaciones gráficas, fortaleciendo su comprensión visual de los conceptos.
• Actividad de completar espacios en blanco: Un educador crea una actividad en Wordwall donde los estudiantes deben completar espacios en blanco en ecuaciones o expresiones algebraicas. Esto les permite practicar y reforzar las reglas y técnicas de manipulación de polinomios y ecuaciones lineales.

Ejemplos de uso de Google Forms:

• Cuestionario de evaluación de álgebra polinomial: Un educador crea un cuestionario en Google Forms con preguntas de opción múltiple y de respuesta corta para evaluar el conocimiento de los estudiantes sobre temas como factorización de polinomios, suma y resta de expresiones algebraicas, etc.
• Formulario de recopilación de datos: Un educador utiliza Google Forms para recopilar datos de los estudiantes, como sus respuestas a problemas específicos de álgebra polinomial y lineal. Esto permite al educador evaluar el progreso de los estudiantes e identificar áreas en las que necesitan más apoyo.
• Formulario de autoevaluación y retroalimentación: Los estudiantes completan un formulario de autoevaluación en Google Forms donde pueden evaluar su propio desempeño y comprensión en álgebra polinomial y lineal. El educador utiliza los resultados del formulario para proporcionar retroalimentación personalizada y guiar a los estudiantes en su aprendizaje.

Figura 9
Uso de recursos tecnológicos por estudiantes de Matemáticas

Nota. Fotografías tomadas por los autores

Enseñanza de estrategias de resolución de problemas

Enfocarse en enseñar a los estudiantes estrategias efectivas para resolver problemas algebraicos. Esto implica proporcionarles un conjunto de pasos y técnicas que pueden utilizar para abordar diferentes tipos de problemas. Al enseñar estrategias de resolución de problemas, los estudiantes adquieren habilidades de pensamiento crítico y aprenden a abordar los desafíos algebraicos de manera más estructurada y metódica.

Fomento de la colaboración y discusión

El trabajo en grupo permite a los estudiantes compartir ideas, plantear preguntas y resolver problemas de manera conjunta. Esto fomenta una comprensión más profunda y ayuda a los estudiantes a abordar diferentes perspectivas y enfoques para resolver problemas algebraicos.

El fomento de la colaboración y discusión en Álgebra Lineal se realizó a través de un trabajo de fin de curso, en conjunto con la asignatura de Probabilidades II, a través de un documento mediado de apoyo para futuros estudiantes de matemáticas, con un enfoque por competencias, que aborda los principales temas de la asignatura de Tópicos de Teoría de Probabilidad, específicamente la Convergencia de sucesiones de variables aleatorias y los Teoremas fundamentales de Probabilidad. Asimismo, se exploran las aplicaciones en el Álgebra Lineal, con un enfoque en la representación de Bézier mediante polinomios y las curvas y superficies paramétricas. Siendo uno de los propósitos del trabajo de fin de curso desarrollar habilidades y competencias en la resolución de problemas y la toma de decisiones, a través de la aplicación de los conceptos teóricos a situaciones prácticas.

A partir, del documento mediado se potencializan las siguientes habilidades y destrezas.

• Analizar y comprender los conceptos y teoremas relacionados con la Convergencia de sucesiones de variables aleatorias y los Teoremas fundamentales de Probabilidad.
• Identificar los diferentes tipos de convergencia en la Teoría de Probabilidades y su aplicación en la resolución de problemas prácticos.
• Aplicar la Desigualdad de Chebishev y el Teorema de Bernoulli y de Poisson en la estimación de la probabilidad de eventos aleatorios.
• Comprender la Generalización de la Ley de los grandes números y su aplicación en la resolución de problemas prácticos.
• Comprender el Teorema local de DeMoivre-Laplace y el Teorema central de límite para aproximar la distribución de una variable aleatoria a una distribución normal.
• Analizar y comprender las aplicaciones en el Álgebra Lineal, con un enfoque en la representación de Bézier mediante polinomios y las curvas y superficies paramétricas.
• Aplicar los polinomios de Bernstein y el algoritmo de Casteljau en la representación y el cálculo de puntos en curvas y superficies de Bézier.
• Resolver problemas y tomar decisiones a través de la aplicación de los conceptos teóricos a situaciones prácticas en la Teoría de Probabilidades y el Álgebra Lineal.
• Trabajar en equipo, comunicar de manera clara y efectiva los resultados y conclusiones obtenidos de las soluciones a los problemas planteados.

Figura 10
Estudiantes de IV año entregando documento mediado pedagógicamente sobre aplicaciones del Álgebra Lineal en Probabilidades II

Nota. Fotografías tomadas por los autores

 

CONCLUSIONES

 

El álgebra polinomial y lineal presenta diversos desafíos que pueden dificultar el aprendizaje y dominio de estos temas. Sin embargo, mediante el uso de soluciones pedagógicas efectivas, es posible superar estos desafíos y ayudar a los estudiantes a desarrollar habilidades sólidas en el álgebra.

La abstracción y conceptualización algebraica requieren que los estudiantes desarrollen habilidades de pensamiento abstracto y la capacidad de generalizar patrones y reglas. La manipulación algebraica implica la habilidad de realizar operaciones y simplificar expresiones de manera precisa y eficiente. La aplicabilidad del álgebra se puede mejorar proporcionando ejemplos concretos y aplicaciones prácticas en diversos campos.

Además, la complejidad en las demostraciones algebraicas puede abordarse mediante un enfoque gradual, el uso de recursos tecnológicos y la enseñanza de estrategias de resolución de problemas. Fomentar la colaboración y la discusión entre los estudiantes también puede fortalecer su comprensión y habilidades algebraicas.

Al implementar estas soluciones pedagógicas, los educadores pueden ayudar a los estudiantes a desarrollar una comprensión más profunda y práctica del álgebra polinomial y lineal. Esto les permitirá aplicar estas habilidades en diferentes contextos académicos y profesionales, así como mejorar su capacidad para resolver problemas de manera efectiva y realizar demostraciones lógicas.

En última instancia, superar los retos y desafíos en el álgebra promueve un aprendizaje significativo y empodera a los estudiantes para que utilicen el álgebra como una herramienta poderosa en su educación y en su vida cotidiana.

 

REFERENCIAS

 

 

ANEXOS

 

Anexo A. Carta de Autorización de uso de Imagen (o datos personales)

Anexo B. Documento Mediado de Aplicaciones del Álgebra Lineal y Probabilidades II

Nota. Documento mediado en el siguiente enlace: http://dx.doi.org/10.13140/RG.2.2.35826.07366