Harvin Joel Bonilla Escoto¹

¹ Dirección de Concesiones – Autoridad Nacional del Agua, ANA.

RESUMEN

La sequía es uno de los fenómenos climatológicos de mayor repercusión a nivel social, económico y ambiental en todo el mundo. Ese es el caso de los municipios en la zona de estudio, la sub-cuenca parte alta del Río Grande de Matagalpa, que han sido clasificados según su afectación agroclimática de sequía como zonas de incertidumbre y riesgo. Por lo que el objetivo de este estudio fue el generar mapas de períodos de retorno asociados a sequías anuales moderadas y severas utilizando el Análisis Regional de Frecuencia basado en la estadística de L-Momentos. A partir de las observaciones de precipitación en las 19 estaciones analizadas se conformaron tres regiones candidatas a regionalización: Norte, Centro y Valle. Sin embargo, el Análisis Regional de Frecuencia solo pudo hacerse en dos regiones a partir de una reconfiguración. Se determinó que las observaciones de las regiones Centro y Valle se ajustan bien a las distribuciones Normal Generalizada (GNO) y Pearson tipo III (PE3), respectivamente, por lo que se infiere que existe una alta heterogeneidad en la amenaza a sequías en la zona. Los períodos de retorno tanto para sequías moderadas como severas en la subcuenca de estudio aumentan de Oeste a Este y a mayor altitud. Las sequías moderadas tienen períodos de retorno que varían desde < 5 hasta 20 años; mientras que las severas varían desde 5 hasta > 50 años. Las áreas más susceptibles desde el punto de vista de recurrencia de sequía se localizan hacia el Noroeste y Oeste, cerca de la comunidad Quebrada honda.

Palabras clave: Análisis regional de frecuencia, L-Momentos, sequía, parte alta del Río Grande de Matagalpa.

ABSTRACT

Drought is one of the climatological phenomena of greater impacts at social, economic and environmental level in the whole world. That is the case in the municipalities from the study zone, the sub-basin upper part Río Grande de Matagalpa, which have been classified based upon their agroclimatic affectation of droughts as uncertain and risk zones. The present study aims to generate maps of periods of return associated with a moderate and severe annual droughts using the Regional Frequency Analysis based on the statistics of L-Moments. From the precipitation observations in the 19 analyzed stations, three candidate regions were formed: North, Center and Valley. However, the Regional Frequency Analysis was made for two regions after a rearrangement. It was determined that the observations from the Center and Valley regions were best fitted to the Normal Generalized (GNO) and Pearson type III (PE3) distributions, respectively, implying a high heterogeneity of the drought hazard in the sub-basin. The periods of return for both moderate and severe droughts in the sub-basin increase from West to East and at higher altitudes. Moderate droughts have periods of return that vary from < 5 to 20 years; while for severe droughts vary from 5 to > 50 years. The most susceptible areas in terms of drought recurrence are located towards the Northwest and West of the study zone, near the community Quebrada Honda.

Key words: Regional Frequency Analysis, L-Moments, drought, upper part of the Río Grande de Matagalpa.

INTRODUCCIÓN

La sequía es uno de los fenómenos climatológicos de mayor repercusión a nivel social, económico y ambiental en todo el mundo. Según Below, Grover-Kopec, & Dilley (2007), las sequías causaron más del 50% del total de muertes debidas a desastres naturales entre los años 1900 y 2004, representaron el 35% de la población afectada por desastres y el 7% de las pérdidas económicas, después de las inundaciones y los terremotos.

Según Global Water Partnership - GWP (2016), durante la sequía ocurrida en Nicaragua en el 2014 se registraron pérdidas de 44,000 manzanas de maíz y 26,073 manzanas de frijol, afectando a 40,000 familias de 32 municipios. Por su parte, el Ministerio Agropecuario y Forestal – MAGFOR, (2002) clasifica a los municipios de Ciudad Darío y Sébaco según su afectación agroclimática de sequía como zonas de incertidumbre, mientras, municipios tales como la ciudad de Matagalpa y Terrabona se clasifican como zonas de riesgo. Todos los municipios antes mencionados se encuentran dentro de los límites de la subcuenca parte alta del Río Grande de Matagalpa. Pese a la importancia que la sequía reviste en la subcuenca y su impacto en los diferentes sistemas de cultivos persiste un factor que agudiza aún más el problema y es la incertidumbre para caracterizar su intensidad, duración, severidad y muy especialmente su frecuencia de ocurrencia.

La generación de mapas de retorno de sequía constituye una de las herramientas útiles para la toma de decisiones en las políticas públicas referentes a la mitigación de los efectos que se derivan del fenómeno de la sequía (Nuñez, Verbist, Ramírez , & Hallack, 2010). Sin embargo, las características propias de las regiones, la gran variabilidad temporal y espacial de las precipitaciones, la influencia de factores externos, tales como El Niño y la reducida disponibilidad de registros de adecuada extensión, imponen ciertas restricciones a la elección del método más adecuado de ajuste probabilístico.

En este estudio se aplicó la metodología denominada Análisis Regional de Frecuencia basada en la estadística de L-Momentos, con el objetivo de generar mapas de período de retorno asociados a una sequía anual moderada y severa asumida como la reducción del 30 y 40% de la precipitación normal respectivamente.

Esta metodología se ha aplicado en estudios de sequías meteorológicas e hidrológicas en muchos países como México (Hallack-Alegria & Watkins Jr , 2007), Turquía (Yurekli & Anli, 2008), Chile (Nuñez, Verbist, Ramírez , & Hallack, 2010) así como para comparar con otras alternativas de regionalización en el estudio de sequías en Europa (Tallaksen & Hisdal, 1999) y para la elaboración del Atlas de Sequía de EE.UU. (IWR, 1995), citado por Nuñez, Verbist, Ramírez , & Hallack (2010).

MATERIALES Y MÉTODOS

El área de estudio se encuentra ubicada en la parte oriental del departamento de Matagalpa y tiene una extensión aproximada de 2,121.63 km² (Fig. 1). Comprende seis municipios del departamento de Matagalpa (Ciudad de Matagalpa, Sébaco, Darío, Terrabona, San Dionisio y Esquipulas) y el de San José de los Remates (Boaco). Según el CENSO del Instituto Nacional de Información para el Desarrollo (2005), la población del área estudio proyectados para el 2008 fue de aproximadamente 272, 411 habitantes.

En la zona de estudio sobresalen alturas como los cerros Tijerina (913.75 m) en cuya parte superior se observan hileras de pinos que crecen sobre el filo rocoso, Palcila (1,478 m), el Picacho (1,750 m) y San Salvador (1,247 m). Al sur de la ciudad de Matagalpa se localiza la montaña de Apante con su pico culminante Buena Vista (1,442 m). La zona presenta un clima de Sabana Tropical de Altura (Awh). Los relieves del municipio tuvieron origen en el intenso vulcanismo de la era terciaria. En el área media del sistema se presenta una zona bastante seca (<800 mm), condicionada por la presencia de una zona hundida del valle de Sébaco (Ministerio de Recursos Naturales, 2010).

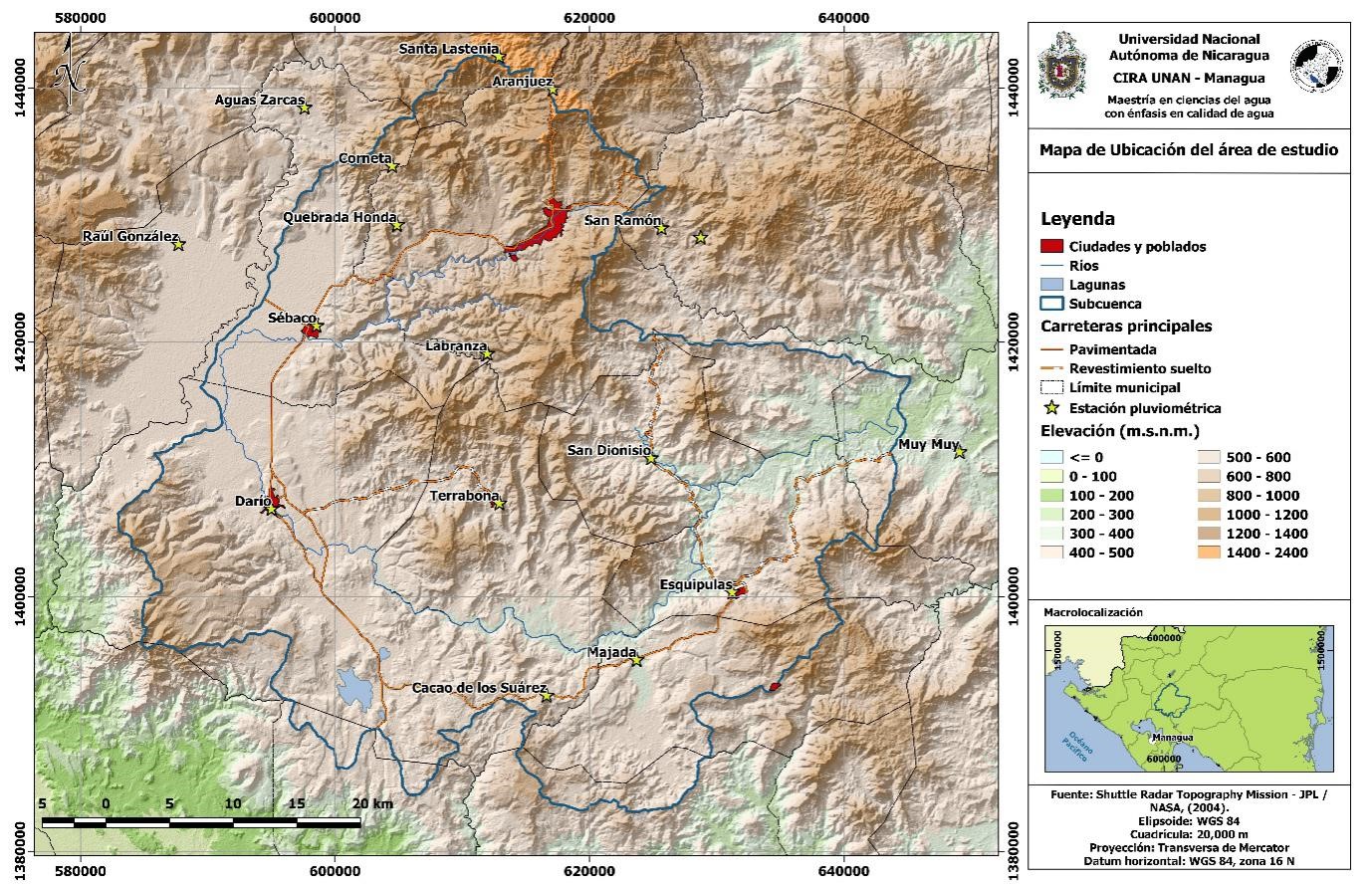
Fig. 1. Mapa de ubicación del área de estudio ubicada en la subcuenca parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia.

Se recopilaron los datos de precipitación anual en 19 estaciones pluviométricas ubicadas dentro y adyacentes a la subcuenca, administradas por el Instituto Nicaragüense de Estudios Territoriales (INETER). La información fue analizada para obtener la estadística básica del conjunto de datos (media, máxima, mínima), se recurrió al análisis de componentes principales y de regresión lineal múltiple entre la longitud geográfica, la altitud y el logaritmo de la Precipitación Media Anual (PMA) de cada estación. Este análisis se realizó con el fin de determinar los factores que intervienen en la distribución de la PMA en la subcuenca.

Posteriormente se empleó el Análisis Regional de Frecuencia (ARF) para estimar los períodos de retorno asociados a sequías clasificadas como moderadas o severas, así como su distribución en el espacio.

El presente estudio se formuló tomando como referencia los trabajos de Hosking y Wallis (1997), Wallis, Schaefer, Barker, & Taylor (2007), Erro (2011), Núñez et al. (2010) y el script en R, escrito por Núñez (2011) y Bonilla-Escoto (2018). Los L-Momentos constituyen un sistema alternativo al método tradicional (momentos convencionales) para describir las formas de las funciones de distribución (Hosking, 1990, citado por Núñez et al., 2010) y surgen de combinaciones lineales de los momentos ponderados probabilísticamente (MPP) introducidos por Greenwood et al. (1979), citado por Núñez et al., (2010).

El Análisis Regional de Frecuencia usando L-Momentos (ARF) está constituido por cinco etapas. a través de L-Momentos que son las siguientes:
     a) Análisis y filtrado de los datos primarios de observaciones.
     b) Identificación de regiones homogéneas.
    c) Selección de la distribución regional de frecuencia.
    d) Estimación de los cuantiles regionales de frecuencia.
    e) Mapeo.

En la primera etapa se determinó si una estación contiene datos confiables, el diagrama de cociente de L-Momentos (diagrama de dispersión entre L-asimetría, L-CV y L-kurtosis), el test de discordancia (Di), un estadístico que compara los L-momentos de cada estación en una región con los del resto de estaciones y los valores medios de dicha región (Erro, 2011); y el valor estimado se compara con un valor crítico (Di crítico) predefinido de acuerdo al número de estaciones evaluadas, cumpliéndose que Di debe ser menor a Di crítico. Para la segunda etapa las regiones fueron conformadas agrupando las estaciones según el análisis de clúster a partir de los atributos físicos de precipitación media anual, elevación sobre el nivel medio del mar y longitud geográfica de las estaciones, considerándole una región homogénea cuando el test de discordancia fuese menor al valor crítico y la prueba de heterogeneidad fuese menor de 2 (H1 < 2). Según Chen, Huang, Shao, & Xu (2006) el valor de la prueba de heterogeneidad se obtiene de la simulación usando una distribución flexible (Distribución de cuatro parámetros: Kappa) con el promedio de los cocientes de L-Momentos. En la tercera etapa se determina la distribución de probabilidad regional de cada región homogénea empleando la prueba de bondad de ajuste Z^dist, la cual, de acuerdo con Erro (2011), se deduce asumiendo que el valor de L-asimetría es igual al valor medio regional de dicho coeficiente. Se juzga entonces la calidad del ajuste por la diferencia entre el L-kurtosis de la distribución General de Valores Extremos (GEV) y el valor medio regional de L-kurtosis. En la cuarta etapa se estimaron los cuantiles asociados a un cierto período de retorno. Según Álvarez, Puertas Agudo, Soto, & Díaz-Fierros (1999), para cada una de las estaciones de la región se determinan los primeros cuatro L-momentos y se hacen adimensionales dividiendo cada uno de ellos por la media de serie. Por último, el mapeo de períodos de retorno se generó a partir de la función de densidad de probabilidad, y su relación con una variable predictiva, la precipitación media anual, dada por la siguiente ecuación:

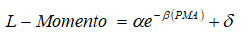
RESULTADOS

Las 19 estaciones analizadas tuvieron un promedio de 27.16 años de registros, siendo la estación de Sébaco la que presenta el mayor número de años (54) y Santa Lastenia la estación que presenta el menor número (13). La precipitación media anual registrada por las 19 estaciones fue de 1,233 mm. Existe un patrón de precipitación anual que aumenta conforme aumenta la longitud geográfica (de Oeste a Este) y la altitud, reflejado tanto en el modelo de regresión lineal múltiple (Fig. 2A), como en el Análisis de Componentes Principales (Fig. 2B). Es importante destacar que la matriz de rotación del componente principal 2 (PC2) establece que existe una alta correlación entre el logaritmo de la precipitación media anual y la longitud geográfica, al ser sus autovalores muy similares entre sí (0.7219 y 0.6781 respectivamente); muy por encima del autovalor obtenido para la variable altitud o elevación (0.1349). Por su parte, el modelo de regresión lineal múltiple indica que la longitud geográfica y la altitud en subconjunto explican el 73% de la variabilidad espacial del logaritmo de la precipitación media anual en la subcuenca (R²=0.73), siendo sus coeficientes iguales a 5.98 × 10^-1 y 1.90 × 10^-4, respectivamente.

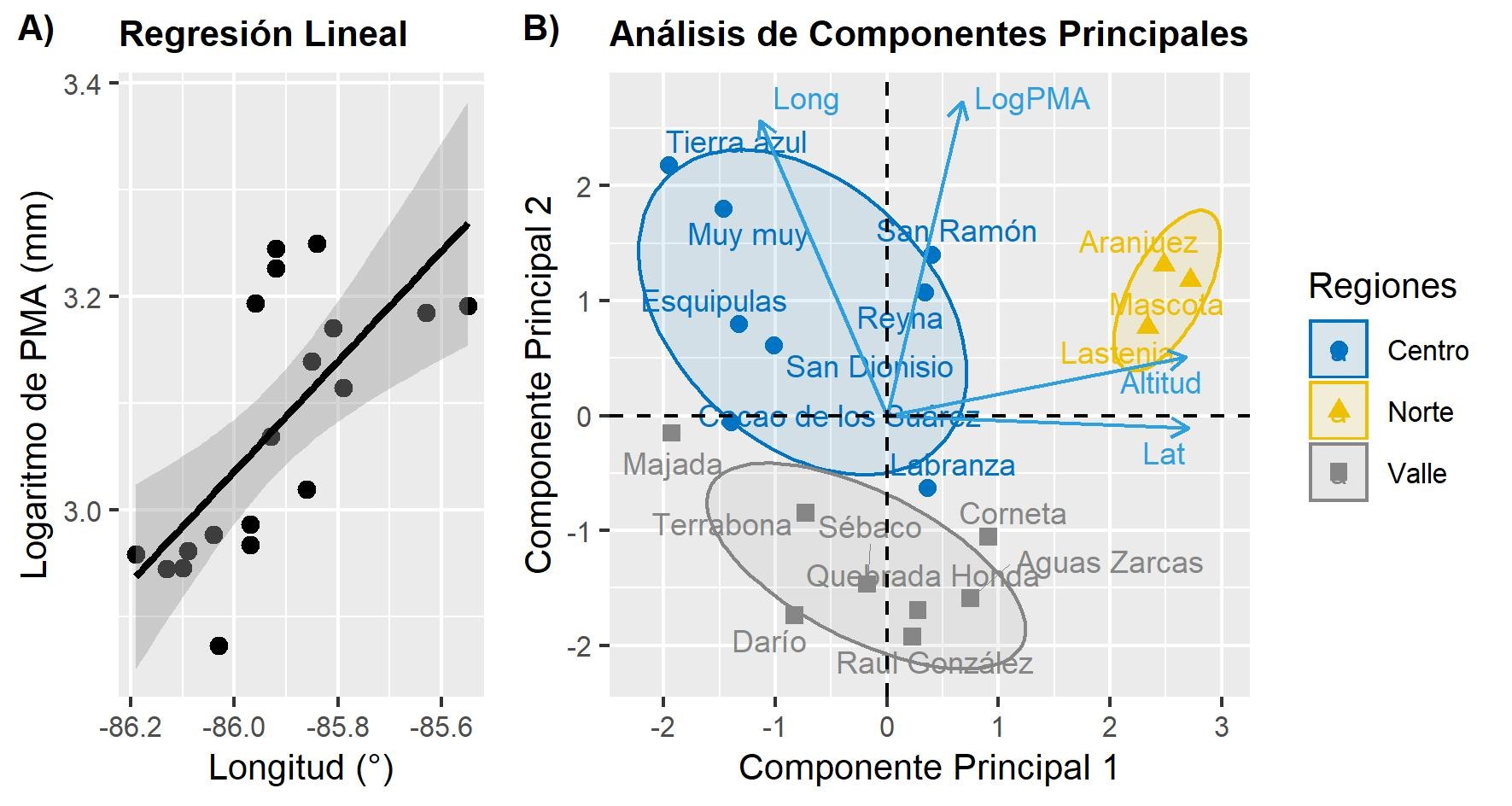
Fig. 2. (A) Representación parcial del modelo de regresión lineal múltiple (Logaritmo de precipitación media anual vs Longitud geográfica) y (B) Análisis de Componentes Principales de los atributos físicos de las estaciones ubicadas en la subcuenca de estudio parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia en base a INETER (2013).

La estación con mayor precipitación media anual de las 19 evaluadas fue la de San Ramón (1,777 mm/año); mientras la de Quebrada honda es la de precipitación media anual más baja de la subcuenca (745.95 mm/año).

La Figura 3, contiene los diagramas de dispersión de los valores de L-asimetría versus L-CV, y L-asimetría versus L-kurtosis, ya que valores incorrectos y demás errores de una muestra quedan reflejados en sus L-momentos. Las estaciones Mascota, Santa Lastenia y San Dionisio se encuentran alejadas de la nube de puntos, siendo representado su centro por el símbolo de una cruz (+) en los diagramas de cociente de L-Momentos (Fig. 3). El análisis de discordancia indica que para 15 o más estaciones el valor crítico (Di) es de 3.

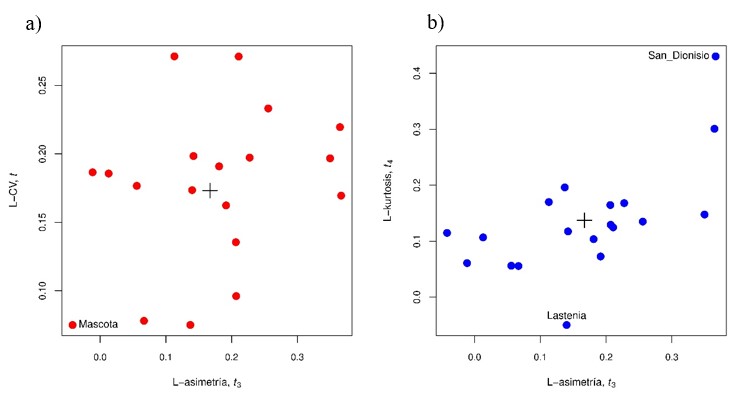
Fig. 3. Cociente L-Momentos iniciales de las estaciones ubicadas en la subcuenca de estudio parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia en base a INETER (2013).

Por lo que la estación de San Dionisio (3.0684) quedó excluida del proceso de Análisis Regional de Frecuencia, por considerársele discordante del resto. Se reiteró el proceso de filtrado sin la estación de San Dionisio lo que dio como resultado que ninguna estación sobrepasó el valor crítico de 3.

El dendograma de la Figura 4 expone gráficamente las distancias de atributos de tal modo que los miembros de cada par de clases que se fusionan son elementos próximos; este proceso continúa sucesivamente entre pares de elementos fusionados hasta que se completan todas las clases. Se establecieron tres (3) regiones homogéneas nombradas Norte (Lastenia, Aranjuez y Mascota), Centro (Muy muy, Tierra azul, Cacao de los Suárez, Esquipulas, Reyna y San Ramón) y Valle (Corneta, Labranza, Quebrada honda, Aguas zarcas, Terrabona, Majada, Darío, Raúl González y Sébaco) para facilitar su identificación. Se aplicó el test estadístico de heterogeneidad, obteniéndose resultados no favorables para la regionalización (H1>2). Debido a esto se prescindió de la región Norte por estar conformada por tres estaciones.

Dado al conocimiento que se tiene de la zona de estudio se trasladó la estación “Labranza” desde la región del Valle hacia la región del Centro porque se localiza sobre un relieve más escarpado que sus homólogas de región, mientras la estación “Santa Lastenia” pasó de la región Norte hacia la región del Centro. Se suprimieron las estaciones de Muy muy y Tierra azul para conformar dos regiones homogéneas denominadas Centro y Valle.

En base a esta reasignación ninguna región sobrepasó el valor crítico de 2 en el test estadístico H1 (H1<2); así mismo, ninguna estación sobrepasó el valor crítico de su Di respectivo, dado el número de estaciones que contiene cada región. Por lo tanto, se procedió a la siguiente etapa.

La Figura 5, representa los trazos de las diferentes distribuciones teóricas (líneas de colores) y los L-Momentos de cada estación en las regiones Centro y Valle, así como la media ponderada de cada región homogénea simbolizada por una cruz (+).

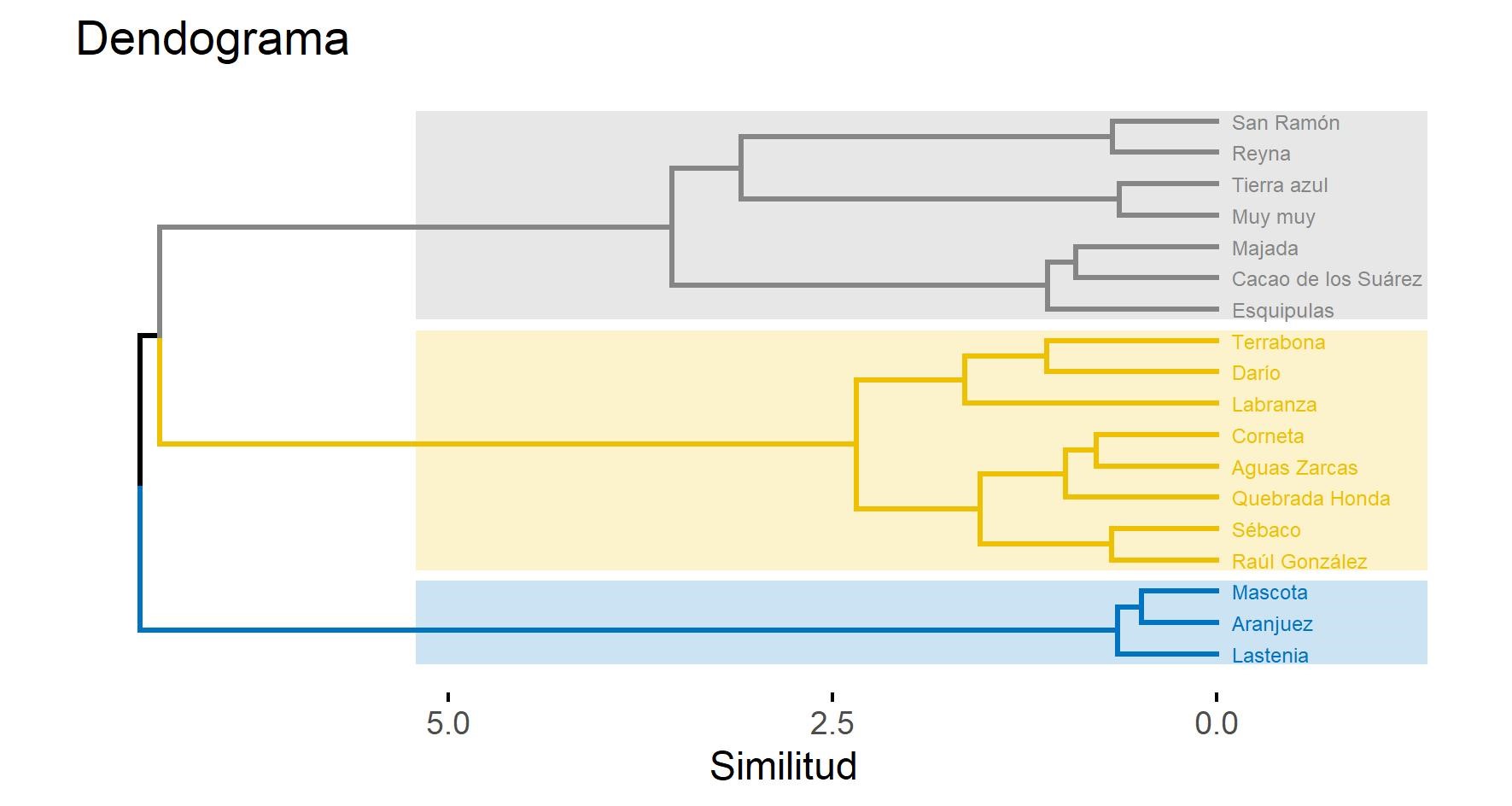
Fig. 4. Dendograma de las estaciones ubicadas en la subcuenca de estudio parte alta del Río Grande de Matagalpa basado en sus descriptores físicos. Fuente: Elaboración propia en base a INETER (2013).

La media ponderada de la región del Centro (Fig. 5a) se acerca a las distribuciones Pearson tipo III (PE3) y Normal Generalizada (GNO). El test estadístico |ZDist| indica que todas las distribuciones son firmes candidatas, a excepción de la distribución Pareto Generalizada (GPA). Se eligió para la región del Centro la distribución Normal Generalizada (GNO) como la más apropiada, debido a que su valor de bondad de ajuste (|ZDist|) es más cercano a cero.

En el diagrama de L-Momentos de la región del Valle (Fig. 5b) la media ponderada de L-Momentos se encuentra próxima a la distribución de Pearson tipo III (PE3). No obstante, otras distribuciones como la Normal Generalizada (GNO) y Valores Extremos Generalizados (GEV) parecen aproximarse a la media ponderada de L-Momentos de la región. Se eligió la distribución Pearson tipo III (PE3) como la distribución que representa a la región del Valle, por ostentar el valor de bondad de ajuste (|Zdist|) más cercano a cero.

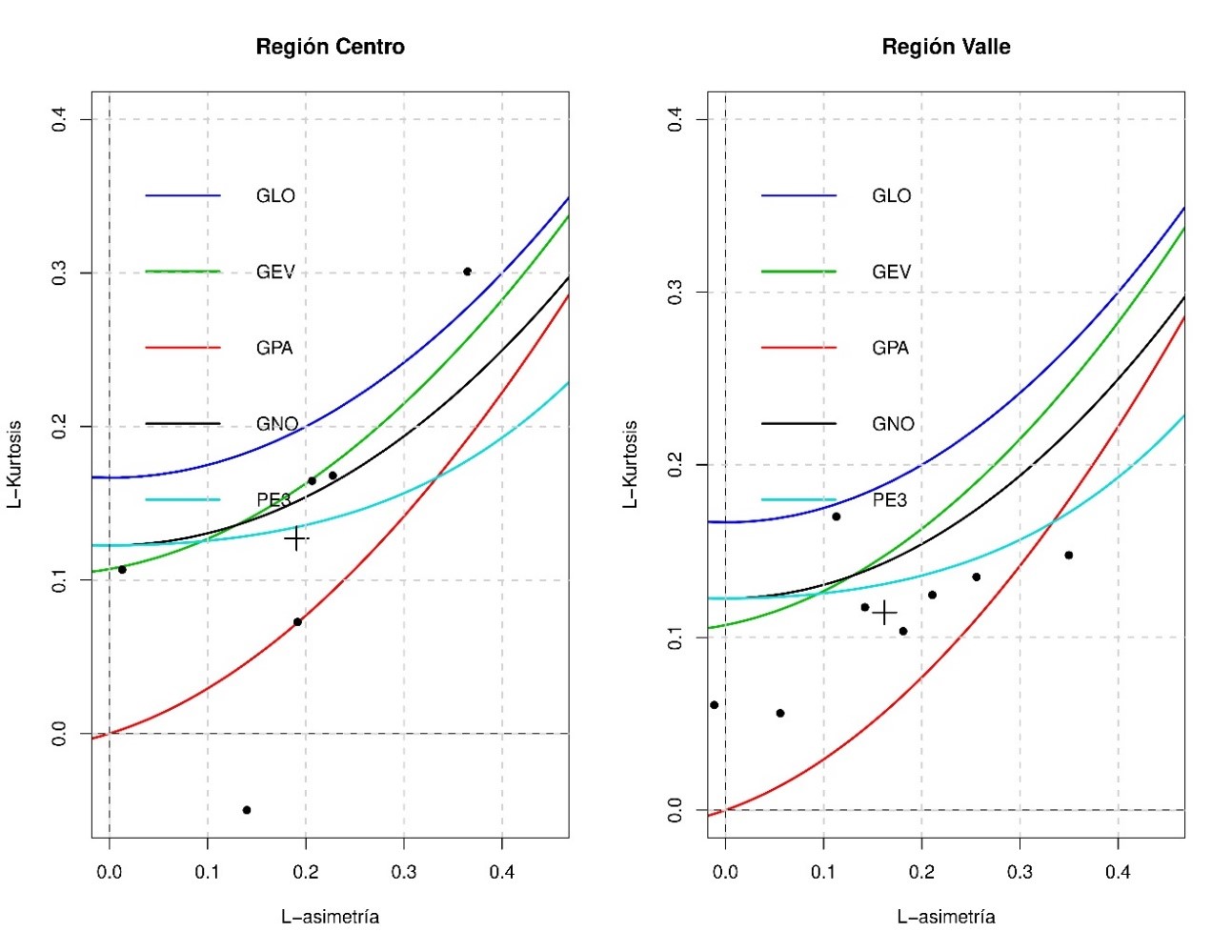
Fig. 5. Diagrama de L-Momentos de las regiones Centro (a) y Valle (b) de la zona de estudio subcuenca parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia en base a INETER (2013).

La Precipitación Media Anual (PMA) y el Coeficiente de Variación Lineal (LCV) de la subcuenca presentan un comportamiento exponencial decreciente con parámetros α=0.3, β=-0.000895 y δ=0.068624. Dicha relación facilitó el mapeo de los períodos de retorno de sequía con reducción de la precipitación respecto a la media histórica del 30 % (moderada) y del 40 % (severa).

Existen áreas dentro de la subcuenca (52% del área total) que poseen períodos de retorno cortos asociados a sequías moderadas (< 5 años) ubicados en el Valle de Sébaco y adyacente a éste (Fig. 6). El 46% del área total de la subcuenca presenta períodos de retorno de sequías moderadas entre 5 y 10 años.

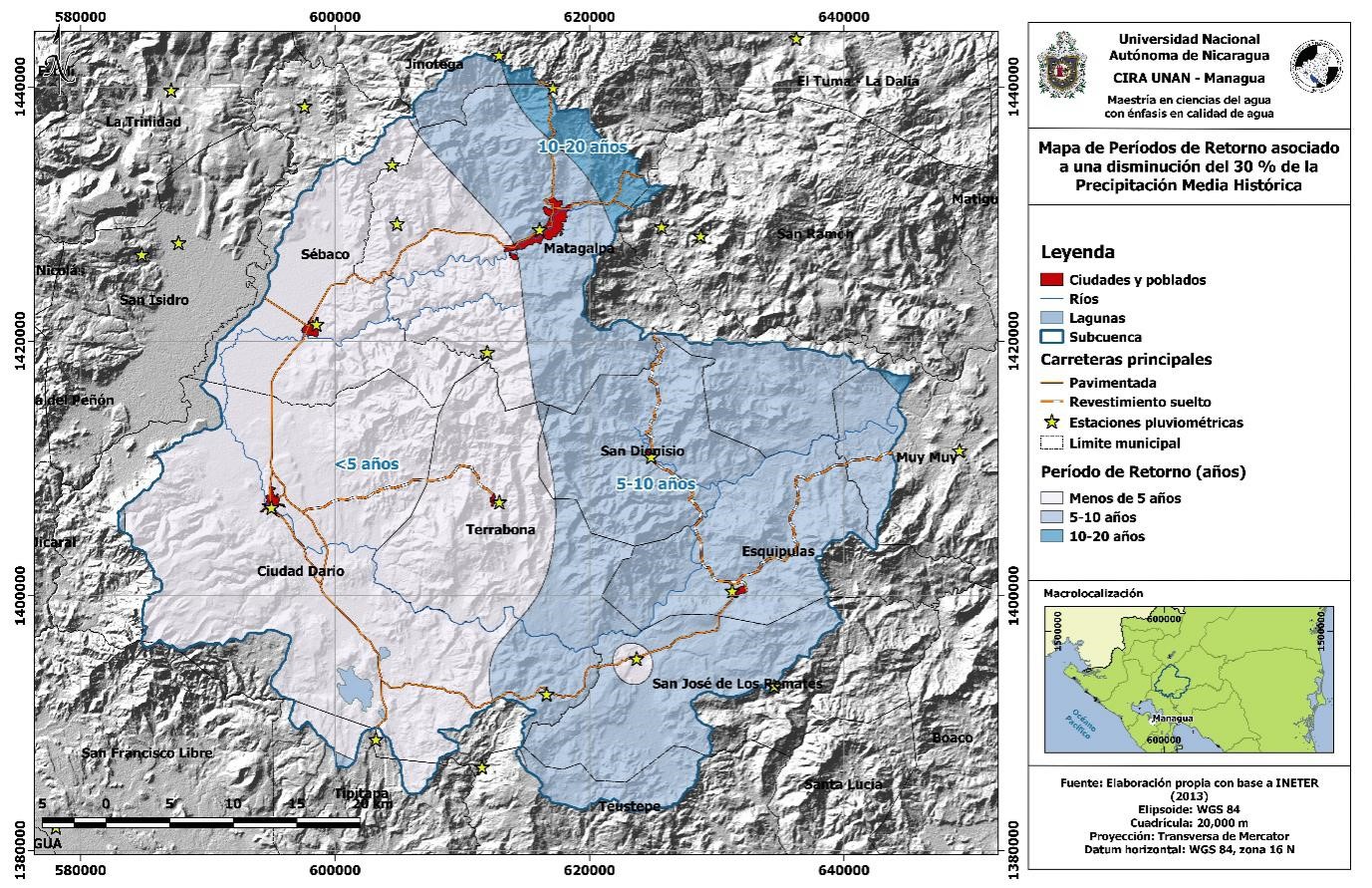
Fig. 6. Mapa de períodos de retorno asociados a una sequía moderada en la zona de estudio subcuenca parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia con base a INETER (2013).

Por otro lado, las sequías clasificadas como severas son menos recurrentes en la subcuenca, encontrándose los períodos de retorno más largos hacia el Noreste (Fig. 7). Es importante destacar que el 48% del área total de la subcuenca posee períodos de retorno comprendidos entre 10 y 20 años para sequías severas.

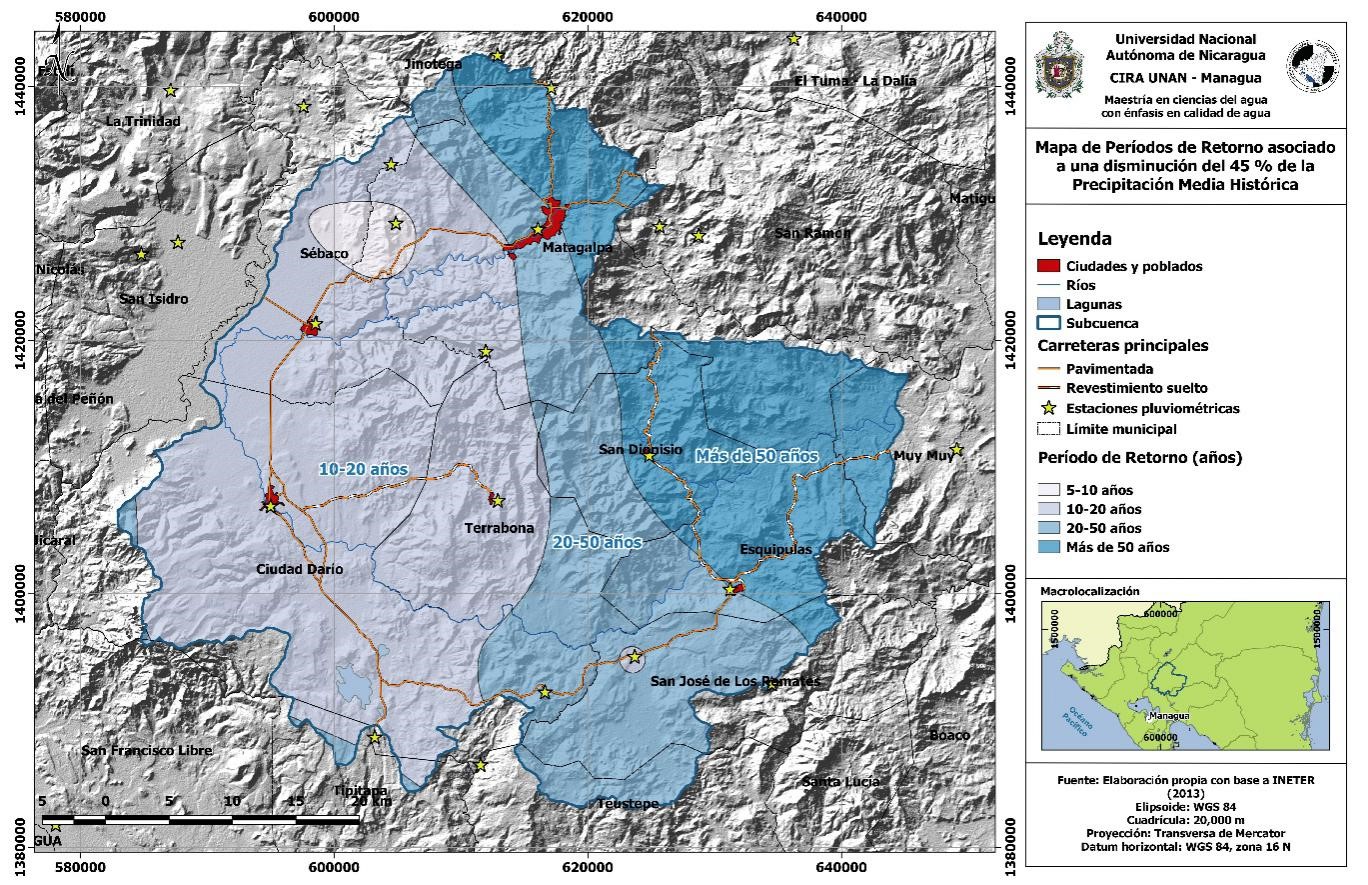
Fig. 7. Mapa de períodos de retorno asociados a una sequía severa en la zona de estudio subcuenca parte alta del Río Grande de Matagalpa. Fuente: Elaboración propia con base a INETER (2013).

Es importante destacar que ciertas áreas poseen menor recurrencia de sequías severas con períodos de retorno ≤ cinco años, tal y como ocurre en la parte noroccidental de la subcuenca en la zona adyacente a la comunidad de Quebrada honda, localizada entre las ciudades de Matagalpa y Sébaco. En esta zona no solo se registran los períodos de retornos más cortos, sino también las precipitaciones más bajas de la subcuenca.

DISCUSIÓN

El patrón existente en donde la precipitación media anual aumenta conforme lo hace la longitud y altitud se debe a la influencia que ejerce el relieve y la orientación de la cordillera Dariense con respecto al flujo predominante producido por los vientos alisios del Noreste. Dicho patrón ha sido reportado por Instituto Nicaragüense de Estudios Territoriales - INETER (2005) y Vargas (2004). Según Vargas (2004), la región denominada núcleo seco de Estelí a Sébaco es una meseta en abrigo, donde el flujo del alisio del Noreste es bloqueado por las cordilleras Dariense e Isabela, y al alisio del Suroeste lo bloquea la cordillera Central. Pagney (1976) opina que el flujo alisio del Noreste y del Suroeste unida a la termoconvección aportan la humedad necesaria para que se produzcan las lluvias en el istmo centroamericano, donde el factor relieve es un mecanismo que la favorece. En este sentido, los cambios en los patrones de flujo tanto de los vientos alisios del Noreste como del Suroeste provocan la aparición de eventos extremos, siendo El Niño/Oscilación del Sur (ENSO) el fenómeno al cual típicamente se relaciona la aparición de la sequía en Nicaragua y por tanto en la subcuenca de estudio. De acuerdo con Capel (1999) durante la aparición de ENSO los vientos alisios del Noreste tiende a debilitarse, e incluso llegan a colapsarse, e invierten su rumbo, soplando entonces hacia el Oeste sobre Indonesia y el Pacífico central, observándose, a modo de efecto de péndulo, una afluencia de agua anormalmente caliente sobre las costas occidentales de América del Sur y en el Pacífico tropical oriental.

Según Núñez et al., (2010), la agrupación de estaciones en regiones homogéneas tiene su justificación en el sentido de que lo que se busca es agrupar estaciones cuyo origen de la lluvia sea el mismo, por lo que en la subcuenca en estudio se puede identificar la existencia de dos sistemas. Por un lado, la región denominada Centro se asocia a las precipitaciones originadas por el efecto orográfico en zona barlovento; y la región denominada Valle a las originadas por el efecto orográfico en zona sotavento, caracterizado este último por el poco contenido de humedad que dejan transitar las principales elevaciones del área. Según Vargas (2004), las cordilleras de la zona central de Nicaragua funcionan como una barrera que bloquea el paso de la humedad que aportan los vientos alisios del Noreste, cayendo en barlovento en el lado del Caribe (Este del país).

La Precipitación Media Anual (PMA) y el Coeficiente de Variación Lineal (LCV) de la subcuenca presentan un comportamiento exponencial decreciente. Núñez et al., (2010), argumenta que los L-Momentos presentan una relación monótonamente decreciente a medida que la magnitud de la precipitación anual aumenta. Resultados similares fueron reportados en estudios realizados en Chile por Núñez et al., (2010) y en México por Hallack-Alegria y Watkins (2007). Sin embargo, dicha relación no es única ya que según Wallis et al., (2007), se han usado diferentes expresiones matemáticas para obtener estimaciones espaciales utilizando los L-Momentos y la precipitación media anual, como son cuadrática, exponencial decreciente y logarítmica.

Por lo cual, los factores que afectan el comportamiento de la precipitación, afectan de igual manera a la sequía en cuanto a su frecuencia, encontrándose períodos de retornos más cortos donde las precipitaciones anuales fueron menores dentro de la subcuenca (zona noroccidental). La distribución espacial de los períodos de retorno es coherente con trabajos realizados en el Norte de Chile por Núñez et al., (2010), donde se determinó que a mayor aridez, mayor recurrencia de eventos de sequía meteorológica clasificados como severos.

CONCLUSIONES

La precipitación media anual en la subcuenca parte alta del Río Grande de Matagalpa es directamente proporcional a la longitud geográfica y la altitud.

El comportamiento heterogéneo de amenaza de sequía fue comprobado por el establecimiento de las regiones Centro y Valle, las cuales se ajustan a las distribuciones Normal Generalizada (GNO) y Pearson tipo III (PE3).

Los períodos de retorno tanto para sequías moderadas como severas en la subcuenca parte alta del Río Grande de Matagalpa aumentan de Oeste a Este y a mayor altitud.

Las sequías moderadas en la subcuenca parte alta del Río Grande de Matagalpa tienen períodos de retorno que varían desde < 5 años hasta 20 años, mientras las sequías severas tienen períodos de retorno que varían desde 5 años hasta > 50 años.

Las áreas más susceptibles desde el punto de vista de recurrencia de sequía en la subcuenca se localizan hacia el Noroeste y Oeste de la misma, alrededor de la comunidad de Quebrada honda.

AGRADECIMIENTOS

El autor desea agradecer a las siguientes personas, tanto por sus aportes técnicos, como por su tiempo y dedicación al presente proyecto de investigación, así mismo a las instituciones que representan:

Yelba Flores, del Centro para la Investigación de los Recursos Acuáticos de Nicaragua (CIRA/UNAN-Managua), Universidad Nacional Autónoma de Nicaragua, Managua, Nicaragua.

Francisco Chavarría, de la Facultad Multidisciplinaria Regional de Matagalpa, Universidad Nacional Autónoma de Nicaragua, Matagalpa, Nicaragua.

Agustí Forguet, de la Universidad Politécnica de Cataluña (UPC). Jordi Girona, Campus Nord, UPC Barcelona Tech, Barcelona, España.

REFERENCIAS

Álvarez, M., Puertas Agudo, J., Soto, B., & Díaz-Fierros, F. (1999). Análisis regional de las precipitaciones máximas en Galicia mediante el método del índice de avenida. Ingeniería del agua, 6(4), 379-386.

Below, R., Grover-Kopec, E., & Dilley, M. (2007). Documenting drought-related disasters: A global reassessment. The Journal of Environment & Development,. 3(16), 328-344.

Bonilla, H. (2018). Análisis regional de precipitaciones anuales para la propuesta de estrategias productivas frente a la amenaza de sequía, parte alta de la cuenca del río Grande de Matagalpa. Tesis de Maestría, Universidad Nacional Autónoma de Nicaragua (UNAN), Centro para la Investigación en Recursos Acuáticos de Nicaragua (CIRA/UNAN-Managua), Managua.

Capel, J. (1999). El fenómeno ENSO (El Niño. Oscilación del sur) en 1997-1998: alteraciones climáticas inducidas en el mundo. Nimbus:. Revista de climatología, meteorología y paisaje(3), 37-62.

Chen, Y., Huang, G., Shao, Q., & Xu, C. (2006). Regional analysis of low flow using L-moments for Dongjiang basin, South China. Hydrological Sciences Journal, 51(6), 1051-1064.

Erro, J. (2011). Análisis regional de las precipitaciones diarias extremas en la cuenca del río Arga con R.

GWP. (2016). Análisis socioeconómico del impacto sectorial de la sequía de 2014 en Centroamérica. Global Water Partnership. Tegucigalpa, Honduras: GWP Central America.

Hallack-Alegria, M., & Watkins Jr , D. (2007). Annual and warm season drought intensity–duration–frequency analysis for Sonora, Mexico. Journal of Climate, 20(9), 1897-1909.

Hoskins, J., & Wallis, J. (1997). Regional frequency analysis: An approach based on l-moments. Cambridge University.

Instituto Nacional de Información para el Desarrollo. (2005). Censo 2005. Managua, Nicaragua: Gobierno de Nicaragua. INIDE, Managua.

Instituto Nicaragüense de Estudios Territoriales. (2005). Comportamiento de la Precipitación Media Anual de la República de Nicaragua. Managua, Nicaragua: Gobierno de Nicaragua. INETER.

MAGFOR. (2002). Estrategias para el manejo de la Sequía. Managua, Nicaragua: Gobierno de Nicaragua. Managua: Ministerio Agropecuario y Forestal.

Ministerio de Recursos Naturales. (2010). Caracterización de la cuenca N° 55, río Grande de Matagalpa. Managua, Nicaragua: Gobierno de Nicaragua. MARENA.

Núñez, J. (2011). Regional Frequency Analysis L-moments R Script (RSARFLM v. 5). Centro del Agua para Zonas Áridas y Semiaridas de América Latina y El Caribe (CAZALAC). Centro del Agua para Zonas Áridas y Semiaridas de América Latina y El Caribe (CAZALAC), La Serena, Chile.

Nuñez, J., Verbist, K., Ramírez , J., & Hallack, M. (2010). Guía metodológica para la aplicación del análisis regional de frecuencia de sequías basado en L-momentos y resultados de aplicación en América Latina. Organización de las Naciones Unidas para la educación, la ciencia y la cultura, y el Centro del Agua para Zonas Áridas y Semiáridas de América Latina y el Caribe (Chile)., Office Montevideo and Regional Bureau for Science in Latin America and the Caribbean . Montevideo: UNESCO Office Montevideo.

Tallaksen, L., & Hisdal, H. (1999). Methods for regional classification of streamflow drought series: The EOF method and L-moments. Technical Report 2, ARIDE project.

Vargas, G. (2004). La escala zonal, regional y local en el análisis del régimen pluviométrico del istmo Centroamericano. Revista Reflexiones, 83(1), 31-56.

Wallis, J. R., Schaefer, M. G., Barker, B. L., & Taylor, G. H. (2007). Regional precipitation-frequency analysis and spatial mapping for 24-hour and 2-hour durations for Washington State. . Hydrology and Earth System Sciences, 11(1), 415-442.

Yurekli, K., & Anli, A. S. (2008). Analyzing Drought Based on Annual Total Rainfalls over Tokat Province. International Journal of Natural & Engineering Sciences, 2(2).