I. INTRODUCCIÓN

Tanto la Física como la Matemática, han sido las ciencias más importantes a lo largo de toda la historia de la humanidad, ya sea en los avances científicos o tecnológicos como en el diario vivir, estas se encuentran a pequeña, mediana o gran escala. Desde el principio de los tiempos, personas de mentes brillantes se han interesado por dedicarle toda una vida de investigación tratando de armar el rompecabezas que involucra el mundo de las matemáticas y la física. Dada su gran importancia y la motivación transmitida por estos grandes personajes, se llevó a cabo este proceso de investigación enfocado en el tema de mecánica de fluidos al aplicarse integrales y espacios vectoriales.

Según Mott (2006) “la mecánica de fluidos es el estudio del comportamiento de los fluidos, ya sea que estén en reposo (estática de fluidos) o en movimiento (dinámica de fluidos)” (p.1). En el caso de este artículo se toman en consideración fluidos en movimiento y en su forma líquida y no gaseosa.

Como resultado de este estudio se obtiene una herramienta en físico de carácter práctico experimental que es accesible, eficaz y eficiente que actúe como auxiliar en la demostración de fluidos, miscibles desde el cálculo vectorial, en colaboración a la sociedad, comunidad científica y universitaria. Dentro de su utilidad académica podrá aplicarse a nivel universitario para la fácil demostración y comprensión de dicho tema.

Para llevar a cabo este estudio, se partió de una indagación a profundidad, explotando todos los recursos disponibles, seleccionando con gran escrupulosidad toda la información recopilada, así mismo, las fuentes consultadas para obtener un estudio confiable, teniendo en cuenta la ética profesional, compromisos con el sector beneficiado de brindarles un estudio bien fundamentado y asumiendo las implicaciones de la investigación. Por tanto, se presentará un prototipo de trabajo experimental, dejando en evidencia la existencia de fluidos en nuestro entorno. Así como las diferentes aplicaciones en la sociedad.

Por ello Herrera (2022) plantea:

El saber sobre las ciencias exactas como lo son las Matemáticas al mismo tiempo de ser agradable es importante para interactuar con claridad, eficacia e inteligencia en un mundo lleno de números, fórmulas, ecuaciones, donde esta ciencia se relaciona con otras para dar respuesta a muchas situaciones del mundo real y la necesidad del conocimiento matemático crece cada vez más al igual que su aplicación. En el proceso de enseñanza-aprendizaje, los conocimientos, las herramientas para conocer las formas de hacer las Matemáticas y comunicarla están en constante evolución. (p. 36)

A través del trabajo realizado se pretende beneficiar a la sociedad en general, así mismo a docentes y estudiantes dentro del proceso de enseñanza - aprendizaje. Por medio de la aplicación del prototipo obtenido como resultado del estudio. Por otra parte, puede ser de mucha ayuda para dar lugar a un determinado estudio, sirviendo como referencia o para aportar a alguna idea.

Uno de los aspectos relevantes en esta investigación es la interdisciplinaridad que se debe abordar para lograr fortalecer el conocimiento de otras ramas de la ciencia. Contribuyendo en el desarrollo de la comprensión de la Física y las Matemáticas de forma clara y precisa, reforzando los saberes de las entidades interesadas en esta investigación.

II. MÉTODOS

2.1 Tipo de Estudio

Este es un estudio de carácter descriptivo, pues bien, no depende de encuestas, ni de procedimientos estadísticos. La búsqueda de información se hizo en función de los procesos descriptivos con relación a la temática en estudio, a fin de caracterizarla correctamente.

Bruto (2010) plantea:

El objetivo de esta investigación descriptiva consiste en llegar a conocer las situaciones, costumbres y actitudes predominantes a través de la descripción exacta de las actividades, objetos, procesos y personas. Su meta no se limita a la recolección de datos, sino a la predicción e identificación de las relaciones que existen entre dos o más variables, también consiste fundamentalmente en caracterizar un fenómeno o situación concreta indicando sus rasgos más peculiares o diferenciadores. (p. 2)

2.2 Enfoque

Este estudio está sustentado en un enfoque cualitativo, ya que se realizó recolección de datos y a continuación se analizó dicha información. Esta investigación también abarca aspectos de enfoque cuantitativo, puesto que se utiliza la recolección y análisis de datos para corroborar preguntas de investigación.

Según Mata (2019) “El enfoque de la investigación está definido como la naturaleza del estudio, la cual manifiesta la recolección de datos como aspectos cuantitativos y abarca el proceso investigativo en todas sus etapas e interpretación de los datos” (p. 1).

2.3 Paradigma

Esta investigación posee un paradigma interpretativo, debido a que se concentra en su objetivo de estudio, asimismo, se utilizarán técnicas de carácter cualitativo. Pues el objetivo de la investigación es la construcción de teorías prácticas.

Según Ayala (2021) “el paradigma interpretativo en investigación es un modelo basado en la comprensión y descripción de lo que se estudia, que es una reacción a los conceptos explicativos y predictivos propios del paradigma positivista”.

2.4 Recolección de la Información

En este estudio, fue necesaria la búsqueda de información, de tipo secundarias. A las cuales se acuden tales como revistas, libros, y páginas de internet que aportan información acerca de integrales, vectores, mecánica de fluidos, fluidos Miscibles y no Miscibles, prototipos. Entre otros.

Para Maranto y González (2015) las fuentes primarias:

Este tipo de fuentes contienen información original es decir son de primera mano, son el resultado de ideas, conceptos, teorías y resultados de investigaciones. Contienen información directa antes de ser interpretada, o evaluado por otra persona. Las principales fuentes de información primaria son los libros, monografías, publicaciones periódicas, documentos oficiales o informe técnicos de instituciones públicas o privadas, tesis, trabajos presentados en conferencias o seminarios, testimonios de expertos, artículos periodísticos, videos documentales, foros. (p.3)

2.5 Análisis de la Información

Para analizar toda la información recolectada, se han realizado una serie de procesos coordinados. Donde se hace la búsqueda de contenido con respecto a la temática en estudio, empleando una exploración alineada a documentos, revistas, libros, blogs, sitios webs, entre otros. Cuyo proceso es realizado pasa a paso, donde cada contenido y fuente de información consultada es analizada minuciosamente y debatida entre los recolectores de dicho proceso investigativo.

III. ANÁLISIS DE RESULTADOS

Se logró analizar de forma secuencial y lógica conceptos teóricos de fluidos miscibles desde el cálculo vectorial, donde se encontró una gran variedad de información. Aunque, muy pocas cuentan con las características necesarias para referenciar. Por lo tanto, se intentó retomar solo la información necesaria sustentada y referenciada.

Figura 1
Fundamentos Teóricos
Nota. Creación Propia a partir del estudio de aspectos teóricos

Se logró construir un prototipo de trabajo práctico experimental para la demostración de existencias de fluidos miscibles desde el cálculo vectorial. Se parte de las siguientes bases teóricas:

Tomando como punto de partida lo planteado por Agüera (2011), el cual menciona que un fluido es una sustancia que se deforma continuamente cuyas magnitudes físicas define el estado en que se encuentra. Por ejemplo: la presión, la temperatura (común a todas las sustancias).

Así mismo Iberti (2000) afirma que “el foco principal de los líquidos miscibles y no miscibles está en la solubilidad de un líquido en otro” (p. 2). Agua y etanol, por ejemplo, son miscible puesto que se mezclan en todas las proporciones. Lo cual implica que serían no miscibles si en cualquier proporción, ellas no forman una solución. Por ejemplo, aceite en agua.

Por otra parte, según Coelho (2019) menciona que un vector es un segmento de recta en el espacio que parte de un punto a otro con dirección y sentido, expresando así las llamadas magnitudes físicas.

También se parte de lo mencionado por De La Cruz (2019) que asegura que la integral es una antiderivada, aunque son complementadas para la determinación de áreas debajo de una curva, aplicando integrales indefinidas en casos donde se requiere calcular el área de dos o más curvas sin valores definidos, igualmente aplicando integrales definidas para saber el área de una sección en específico.

Además, se ha retomado lo estipulado por Cuofano (2022) quien habla de un prototipo como una versión de muestra o simulación para evaluar un proceso o concepto. Asumiendo que un prototipo puede ser tan simple como un boceto de guion gráfico dibujado en papel que captura la experiencia del usuario o tan detallado como una maqueta a gran escala.

A base de los antecedentes de estudio encontrados en esta investigación se realizaron diversos experimentos con fluidos miscibles. A través de este proceso de experimentación se conoció la miscibilidad de dos o más fluidos, así como la no miscibilidad en algunos casos, lo cual se debe a la diferencia de densidades entre los fluidos.

Se analizó la parte vectorial en los fluidos miscibles, desde el punto de vista molecular. Conociendo que las moléculas se mantienen en constante movimiento de forma desordenada, estas se mueven con un sentido, dirección y una velocidad. Por lo tanto, aun siendo un movimiento aleatorio, podría relacionarse a cada molécula con un vector. Ya que, al mezclar dos o más fluidos miscibles, llegaría a formarse un campo vectorial, donde dichos vectores moleculares se mueven hacia todas las direcciones. Aunque, no sería posible hacer un cálculo vectorial como tal, porque se mueven de forma impredecible.

Los fluidos miscibles son más comunes en nuestro entorno que los no miscibles. Por esta razón, se decidió realizar la construcción de un prototipo para poder demostrar la existencia de fluidos miscibles desde el cálculo vectorial. El cual, consiste en una réplica de una piscina tipo maqueta, donde se refleja una de las posibles aplicaciones en nuestra vida cotidiana. Para llevar a cabo la demostración antes mencionada, se tomó como idea base la siguiente explicación encontrada en YouTube en la que se demuestra cómo se pueden aplicar las integrales en el cálculo de fuerza en placas sumergidas causadas por la presión de un líquido (LaMejorAsesoríaEducativa, 2019).

Se construyó el siguiente prototipo, con ayuda de los materiales:

Fluidos miscibles

• lámina de Plywood de 56 cm x 50 cm

• 1 lámina de Plywood de 50 cm x 35 cm

• 1 mayita de 20 cm de largo por 10 cm de ancho.

• 1 pega loca.

• 11 palitos de bambú. 4 de 26 cm de largo, 2 de 15 cm, 1 de 20 cm y 4 de 4 cm de largo, todos con un diámetro de 1 cm.

• 1 palillo de plástico de 30 cm y ½ cm de diámetro.

• 2 yardas de alambre liso de 1/8.

• 1 acuarela.

• 4 ruedas de Plywood de 12 cm de diámetro.

• 2 tornillos de 1 pulgada de largo.

• 1 cubeta transparente de 27 cm de ancho x 41 cm de largo x 24 de alto.

• Agua y cloro.

• 4 foamy color rojo, morado, blanco y rosado.

• 1 spray color celeste.

• 1 placa de Plywood con forma de media circunferencia con un radio de 10 cm

• 4 vasos de plástico transparente.

• Uso de pistola aplacadora de silicón caliente.

• 5 barras de silicón.

• 1 bola plástica pequeña.

• 2 pedazos de alambre de amarre.

Realizando el prototipo a través de los siguientes pasos:

1. 1. Se cortan dos láminas de Plywood, una de 56 cm x 50 cm y otra de 50 cm x 35 cm
2. 2. Se pinta con spray las dos láminas de Plywood, una por ambos lados y la otra solo, por un lado.
3. 3. Se pinta con acuarela la parte superior de la otra lámina de Plywood.
4. 4. Se pegan con silicón y con ayuda de dos tornillos de una pulgada de largo, las dos láminas de Plywood, una en la parte inferior de la cubeta y la otra en la parte superior.
5. 5. Con pega loca se unen los 4 palitos de bambú con medidas de 26 cm de largo en las esquinas inferior y superior del Plywood.
6. 6. Se diseñan los marcos de cada silla con el alambre lizo de 2 yardas.
7. 7. Se cortan 4 láminas de Plywood de 4 cm de ancho por 8 cm de largo.
8. 8. Seguidamente, se procede a forrar las 4 láminas de Plywood con foamy.
9. 9. Luego de esto se pegan las 4 láminas de Plywood con silicón sobre los marcos de silla.
10. 10. Se corta la placa con forma de media circunferencia con un radio de 10 cm.
11. 11. Se pintó la placa de forma media circular de Plywood.
12. 12. Se pegan los dos palitos de bambú en cada esquina de la placa con pega loca y en la parte de en medio de la placa pegamos un palito de bambú con pega loca.
13. 13. Después de haber hecho esto se unen con pega la parte de debajo del palito con la cubeta.
14. 14. La parte de los dos palitos que están pegados hacia arriba de la placa en esos dos palitos amarramos la mayita de voleibol con nailon.
15. 15. Seguidamente, amarramos con alambre de amarre el palillo de plástico atravesado en la parte donde está la placa para sostenerla.
16. 16. Se cortan 4 ruedas de Plywood con medidas de 12 cm de diámetro.
17. 17. Se procedió a forrar con foamy las 4 ruedas de Plywood.
18. 18. Seguidamente, se pegan los 4 palitos de 4 cm de largo con las 4 ruedas de Plywood.
19. 19. Después de haber pegado las ruedas con los palitos se pegan con pega loca sobre la lámina de Plywood.
20. 20. Y por último se forra con foamy de color blanco cada orilla de la cubeta.

Figura 2.
Pasos para construcción del Prototipo de Trabajo Experimental
Nota. Creación Propia a partir de la creación del propio

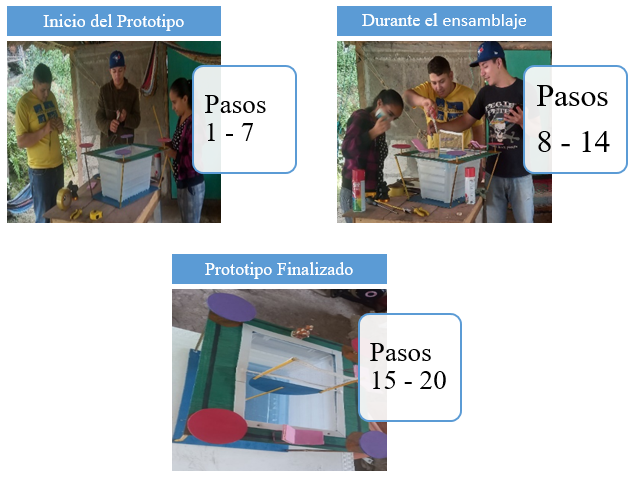
Mediante la observación del prototipo que se muestra en la figura 3, y apoyándose en la figura 4. Se hace el planteamiento del siguiente problema, que sirve de complemento en la demostración: En una piscina replicada a pequeña escala a través de una maqueta, donde las medidas de la piscina son; 27 cm de ancho x 41 cm de largo x 24 de alto. En ella se encuentra una red de voleibol, la cual está sujeta a una placa semicircular que sirve de base, con un radio de 10 cm. ¿Por lo tanto, se requiere calcular la fuerza ejercida por el fluido (que sería el agua y el cloro) sobre la placa?

Figura 3.
Prototipo
Nota. Creación Propia, construcción del prototipo con material de fácil acceso

Figura 4.
Simulación del costado paralelo a la placa
Nota. Creación Propia

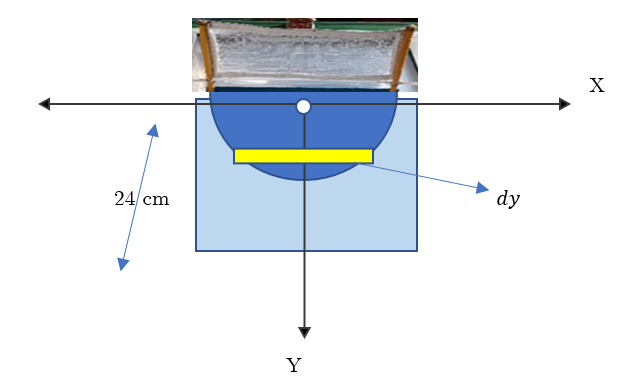
Datos:

Altura = 24 cm

Ancho = 27 cm

Radio de la placa sumergida = 10 cm

Cantidad de agua y cloro = 24 litros

Para iniciar las operaciones se debe tomar en cuenta el primer paso.

Paso 1: Ubicar el sistema de referencia (ejes de coordenadas) en la figura 8, de tal forma que el origen quede en el centro de la placa.

Paso 2: Ubicar un rectángulo tipifico (dy) sobre la placa de la figura 8, el cual debe ser paralelo al nivel del agua, ubicado siempre a una distancia y de eje x, dicho rectángulo se desplazará a lo largo y ancho de la placa al momento de resolver la integral.

Paso 3: Despejar ecuación de la presión para calcular la fuerza del fluido.

Para encontrar la fuerza es necesario despejar la fuerza de la ecuación principal.

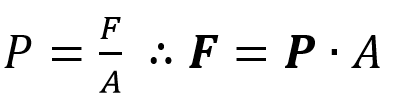
Para conocer la presión se aplica la siguiente formula.

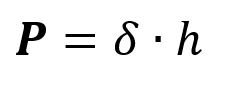
Una vez hecho el despeje nos queda, que la fuerza es igual a la presión por el área, pero en este caso en lugar de p se ubicará $\delta ·h$

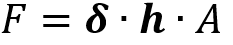
Datos importantes:

Siendo así nos queda una sola fórmula para encontrar la Fuerza. Sustituyendo la presión y el área por su igualdad.

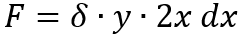
Paso 4: Analizar la ecuación de la circunferencia en función de la figura 8, para trabajar la placa.

En este caso el centro sería (0,0) Por lo tanto c(h,k) = (0,0)

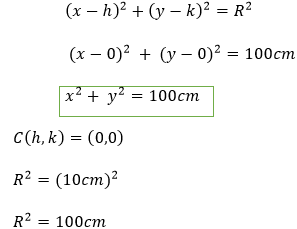
Paso 5: Ya con los datos analizados se puede trabajar la ecuación general de la circunferencia adaptada a la placa sumergida planteada en el problema. Por lo tanto, hay que determinar “x” en función “y”. Reemplazando los valores desarrollamos la ecuación para encontrar el valor de” x”.

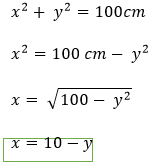
Paso 6: Plantear la integral que nos permite obtener la fuerza.

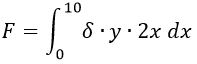
Ya en este punto reemplazamos el valor “x” de para obtener una ecuación más específica.

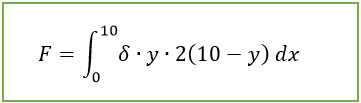
Al analizar el problema planteado anteriormente se logró demostrar la existencia de los fluidos miscibles, que sería la mezcla entre el agua y el cloro vertida en la piscina. De igual manera se encuentra una placa sumergida que sirve de base a la red de vóleibol, entonces haciendo uso de las integrales definidas y algunas fórmulas de física, se alcanzó a demostrar el cálculo de la fuerza ejercida por dicho fluido sobre la placa.

En fin, los resultados más significativos son:

Para que exista una miscibilidad es necesario que ambos fluidos compartan una misma densidad.

En un fluido miscible se puede visualizar la parte vectorial desde el punto de vista molecular, donde cada molécula sería un vector, pues este se mueve con un sentido, dirección y a una velocidad. Aunque no se podría hacer cálculo vectorial como tal porque se mueven hacia todas las direcciones aleatoriamente.

Mediante ecuaciones de mecánicas de fluidos, geometría e integrales definidas, es posible hacer cálculo de la fuerza que ejerce el fluido sobre la placa sumergida representada en la figura 2 y 3.

Además, se conoció el uso gran importancia que tienen los fluidos miscibles en nuestra vida cotidiana.

Entre los factores o variables influyentes que pueden afectar los resultados sería el desconocer el significado de lo que es en sí un fluido, ya que existe una gran gama de químicos que dan lugar a una solubilidad, pero estos no se consideran fluidos. Como por ejemplo el azúcar con el agua, ambos se mezclan, pero el azúcar en su estado natural es un sólido, por lo tanto, no pertenece a los fluidos.

Dentro de las fortalezas se encuentra el trabajo colaborativo entre el grupo de investigación, la comunicación, interés en común por llegar a una buena conclusión y excelentes resultados. Como limitaciones del estudio se puede mencionar el no contar con más de una computadora, pues, esto hace más lento el proceso de investigación, además de la mala calidad de la señal de internet ha sido uno de los obstáculos principales.

Con respecto a los hallazgos encontrados por medio de este estudio se ha indagado con la intención de encontrar un sustento científico que apoye los resultados encontrados, pero no se ha descubierto ninguna publicación similar. Por lo tanto, se deja abierta la posibilidad a futuros investigadores para darle continuidad a la presente investigación, o bien sea en función de mejorar dichos hallazgos. Asimismo, se realizó la búsqueda de argumentos o publicaciones que indiquen lo contrario a los resultados obtenidos del presente trabajo. Pero al igual no se logró encontrar nada relacionado.

Tomando en cuenta los factores que pudieron haber incidido en dichos resultados. Se pueden mencionar el uso de fluidos más comunes y de fácil acceso utilizados para la experimentación. Otro factor sería la combinación con el cálculo vectorial más la relación que involucra álgebra, integrales, mecánica de fluidos y formas de evaluación.

En cuanto al significado del presente trabajo realizado. Está orientado a la construcción de un prototipo práctico experimental, para poder reflejar la existencia de fluidos miscibles desde el cálculo vectorial. Donde se dará una demostración mediante el prototipo de trabajo práctico experimental ya antes mencionados.

La importancia de la presente investigación va más allá de una demostración, ya que se pueden retomar aspectos importantes de los resultados obtenidos para fortalecer investigaciones futuras, o bien sea para darle continuidad a la misma. También puede ser una base fundamental para desarrollar contenido involucrados en la fundamentación teórica y reflejados en la demostración. Por otro lado, puede dar origen a nuevas ideas de utilidad científica.

Cuando se decide emprender un proceso de investigación es porque se quieren conocer resultados, partiendo de las interrogantes que no satisfacen el vacío del conocimiento, por lo tanto, para que este estudio logre alcanzar la satisfacción esperada es necesario realizar todos los procedimientos que conlleva dicha investigación ya antes mencionada, por lo que es de esta manera como se logra conocer, analizar, interpretar, experimentar, debatir sobre la base de los resultados para llegar a una sola conclusión.

Dentro de las implicaciones de la investigación tenemos:

• Comprobar lo planteado en los objetivos del estudio.

• Examinar los resultados obtenidos de todo el proceso.

• Tomar en cuenta las líneas de investigación que son las aplicaciones de las ciencias exactas, matemática aplicada y la física aplicada.

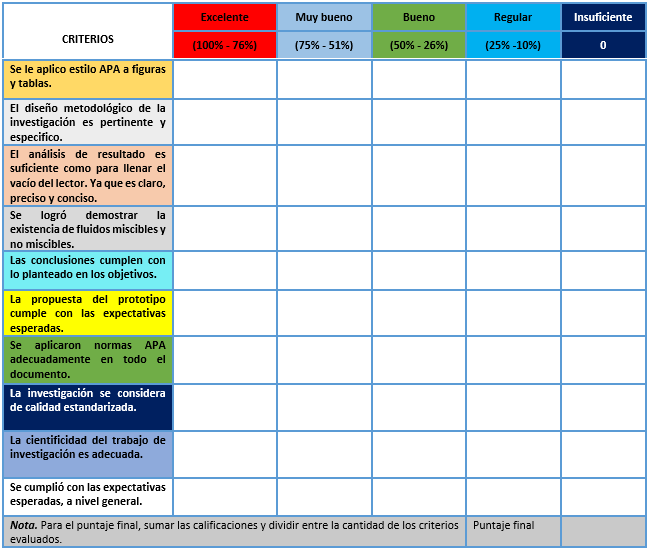
Para la valoración del trabajo de investigación realizado se elaboró una rúbrica evaluativa en la que se podrá calificar desde 0 hasta el 100%. De la misma manera se estará tomando en cuenta la calidad del trabajo realizado. Es decir, para que dicho estudio alcance el 100% de calificación debe tener una buena presentación, coherencia, lógica y sentido, así como los requerimientos necesarios para considerarse un estudio científico. Por tanto, se debe cumplir con los estándares de investigación predeterminados.

Siendo la rúbrica la siguiente:

Tabla 1.

Rúbrica de Evaluación del Trabajo de Investigación

Tabla 1.

Continuación

Nota. Creación Propia

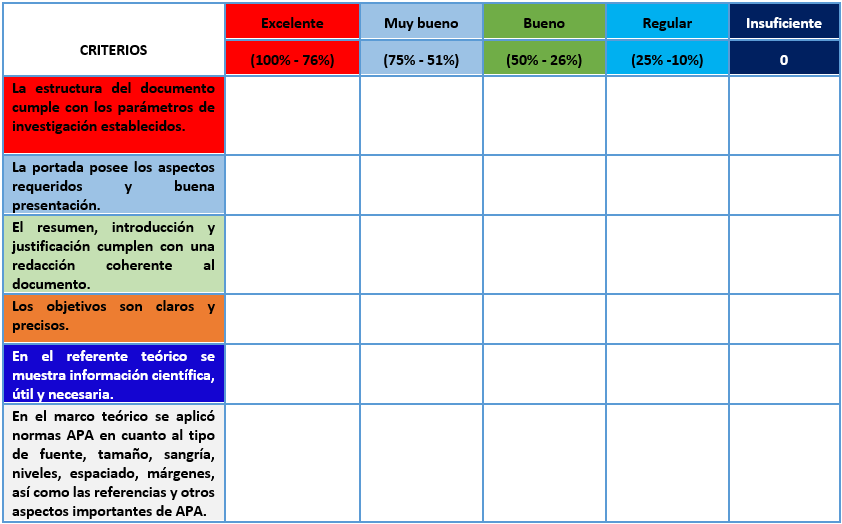
IV. CONCLUSIONES

Mediante la indagación y análisis de conceptos teóricos, empezando con las integrales, se descubrió que la relación existente de forma directa con los fluidos miscibles, no es tan común en situaciones reales. Del mismo modo sucede con la parte vectorial, ya que dichas aplicaciones de vectores están más orientadas a otras situaciones. Aun así, se analizó la parte de la mecánica de fluidos donde se encuentra una gran relación, siento esta rama la encargada de estudiar el movimiento de los fluidos. También se estudió la miscibilidad, lo cual ha sido de fundamental importancia para todo el proceso investigativo, pues, estos son muy comunes en nuestro entorno. También, se estudiaron los conceptos de prototipo que han sido de mucha importancia para lograr establecer demostración eficaz de la temática en estudio.

Una vez obtenido el sustento teórico se logró construir un prototipo plasmado en una maqueta experimental alusiva a una posible situación de nuestra vida diaria. Esta fue elaborada con materiales muy comunes en nuestro entorno y de fácil acceso. Ya finalizada la construcción se realizó el proceso de experimentación donde se logró demostrar la existencia de fluidos miscibles desde el cálculo vectorial.

Sin embargo, es importante mencionar que se llevó a cabo un análisis previo de los fluidos miscibles, a través de la experimentación, dejando en evidencia la existencia de dichos fluidos. No obstante, se ha demostrado que es más común la miscibilidad entre fluidos que la no miscibilidad, esto se debe a lo siguiente; Siempre que dos o más fluidos compartan una misma densidad, se dará una miscibilidad.

Para la evaluación de este estudio en general se elaboró una rúbrica estructurada conforme a los estándares preestablecidos, mediante la cual, se podrá calificar el trabajo de investigación, y así mismo poder identificar aspectos a mejorar en investigaciones posteriores. Además de guiar procesos de estudios que requieran ser evaluados.

Mediante la rúbrica se logró valorar criterios importantes de evaluación que implican, la calidad de documento, el cumplimiento con las normas de investigación, tales como la objetividad y cientificidad del estudio, sumado la coherencia en todos los aspectos del proceso. Así como la interdisciplinariedad en el trabajo realizado al vincular otras ramas de estudio tal y como lo es Álgebra, Cálculo, Estructura de la Materia y Evaluación educativa.

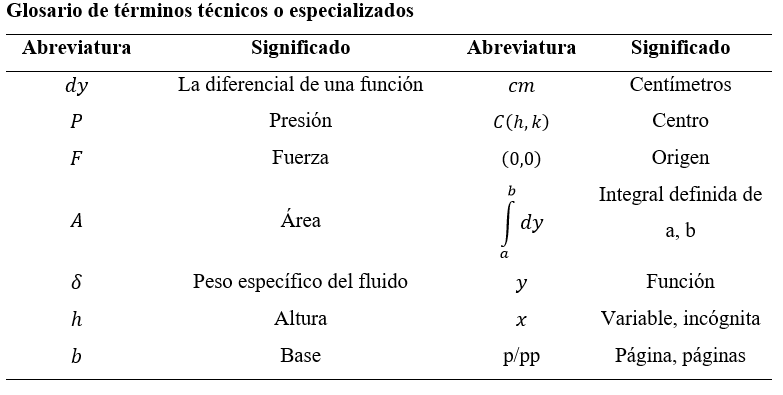
Glosario

REFERENCIAS

Agüera Soriano, J. (2011). MECÁNICA DE FLUIDOS. En J. A. Soriano, DEFINICIONES Y PROPIEDADES (págs. 13-14).

Ayala, M. (19 de enero de 2021). Paradigma interpretativo. Obtenido de Lifeder.com: https://www.lifeder.com/paradigma-interpretativo-investigacion/

Bruto, M. (16 de septiembre de 2010). Conozca 3 tipos de investigación: descriptiva, exploratoria y explicativa. Recuperado el 26 de abril de 2020, de Academia.edu: https://www.academia.edu/8101101/Conozca_3_tipos_de_investigacion

Coelho, F. (1 de enero de 2019). Vector. Obtenido de https://www.significados.com/poesia/

Cuofano, G. (17 de agosto de 2022). FourWeekMBA. Obtenido de https://fourweekmba.com/es/prototipado/

De La Cruz Reyes, L. A. (30 de enero de 2019). Áreas: Aplicaciones de la integral (Matemáticas, física, ingeniería, etc.). Recuperado el 20 de Octubre de 2022, de https://ingenieriaelectronica.org/areas-aplicaciones-de-la-integral-matematicas-fisica-ingenieria-etc/

Herrera Castrillo, C. J. (2022). Metodologías para el aprendizaje por competencias de Ecuaciones Diferenciales aplicadas en Física al utilizar tecnología en la carrera Física Matemática. Revista Torreón Universitario, 11(32), 33-44. Recuperado el 24 de Diciembre de 2022, de https://revistatorreonuniversitario.unan.edu.ni/index.php/torreon/article/view/432/914

Iberti, C. (2000). Líquidos miscibles y no miscibles. ICARITO, Párr. 1-2.

LaMejorAsesoríaEducativa. (6 de septiembre de 2019). Aplicación de las integrales. Cálculo de fuerza en placas sumergidas. [Video]. YouTube. Obtenido de https://www.youtube.com/watch?v=PQ0LxuG8bzg

Maranto Rivera, M., & González Fernández, M. E. (2015). Fuentes de Información. Universidad Autónoma del Estado Hidalgo. Recuperado el 14 de Diciembre de 2022, de https://repository.uaeh.edu.mx/bitstream/bitstream/handle/123456789/16700/LECT132.pdf

Mata Solís, L. D. (7 de mayo de 2019). El enfoque de investigación. Investigaría, 1. Obtenido de https://investigaliacr.com/investigacion/el-enfoque-de-investigacion-la-naturaleza-del-estudio/

Mott, R. L. (2006). Mecánica de Fluidos 6/e. Pearson educación. Recuperado el 03 de Octubre de 2022, de https://acortar.link/librofluidos