Keywords: Calculation, Evaluation, Fluids, Integrals, Prototype

Abstract

This article deals with the subject of experimental practical work prototypes for the demonstration of equations of fluid mechanics by applying integrals and vector spaces. The main objective was to demonstrate through a prototype the existence of miscible fluids from vector calculus. Likewise, theoretical concepts were analyzed in a sequential and logical way, through the investigation of integrals, vectors, fluid mechanics, prototypes, and evaluation rubrics. A replica of a recreational swimming pool was built to demonstrate the application of miscible fluids in daily life, as well as the calculation of the force exerted by a fluid on a submerged plate through definite integrals. It is important to mention that an evaluation rubric was designed for the assessment of the work done. The research was descriptive with a qualitative approach. In the results obtained, it was possible to demonstrate the existence of miscible fluids, in the same way, the equation indicated to calculate the force exerted by a fluid on a submerged plate was adapted, through the interdisciplinarity between subjects of Calculus II, Algebra III, Structure of Matter and Educational Evaluation.

1. INTRODUCTION

Both physics and mathematics have been the most important sciences throughout the history of mankind, whether in scientific or technological advances or daily life, they are found on a small, medium, or large scale. Since the beginning of time, people of brilliant minds have been interested in dedicating a lifetime of research to trying to put together the puzzle that involves the world of mathematics and physics. Given its great importance and the motivation transmitted by these great characters, this research process was carried out focused on the topic of fluid mechanics by applying integrals and vector spaces.

According to Mott (2006), “Fluid mechanics is the study of the behavior of fluids, whether they are at rest (fluid statics) or in motion (fluid dynamics)” (p.1). In the case of this article, fluids in motion and their liquid and non-gaseous form are taken into consideration.

As a result of this study a tool in physics of experimental practical character is obtained that is accessible, effective, and efficient that acts as an auxiliary in the demonstration of fluids, miscible from the vectorial calculation, in collaboration to the society, scientific and university community. Within its academic utility, it can be applied at the university level for easy demonstration and understanding of this subject.

To carry out this study, we started with an in-depth investigation, exploiting all available resources, selecting with great scrupulousness all the information collected, as well as the sources consulted to obtain a reliable study, taking into account professional ethics, commitments with the benefited sector to provide them with a well-founded study and assuming the implications of the research. Therefore, a prototype of experimental work will be presented, showing the existence of fluids in our environment. As well as the different applications in society.

Therefore, Herrera (2022) proposes:

Knowledge about the exact sciences such as mathematics, while being pleasant, is important to interact with clarity, efficiency, and intelligence in a world full of numbers, formulas, and equations, where this science is related to others to respond to many real-world situations and the need for mathematical knowledge is growing more and more as well as its application. In the teaching-learning process, the knowledge, and the tools to know the ways of doing mathematics and communicating it are in constant evolution (p. 36).

Through the work carried out, it is intended to benefit society in general, as well as teachers and students in the teaching-learning process. Through the application of the prototype obtained as a result of the study. On the other hand, it can be of much help to give rise to a certain study, serve as a reference, or contribute to some idea.

One of the relevant aspects of this research is the interdisciplinarity that must be addressed to strengthen the knowledge of other branches of science. Contributing to the development of the understanding of physics and mathematics in a clear and precise way, reinforcing the knowledge of the entities interested in this research.

2. METHODS

2.1. Type of Study

This is a descriptive study since it does not depend on surveys or statistical procedures. The search for information was made based on descriptive processes concerning the subject under study, to characterize it correctly.

Bruto (2010) states:

The objective of this descriptive research consists of getting to know the situations, customs, and predominant attitudes through the exact description of activities, objects, processes, and people. Its goal is not limited to the collection of data, but to the prediction and identification of the relationships that exist between two or more variables; it also consists fundamentally in characterizing a phenomenon or concrete situation by indicating its most peculiar or differentiating features. (p. 2).

2.2. Approach

This study is based on a qualitative approach since data was collected and then analyzed. This research also includes aspects of a quantitative approach, since data collection and analysis are used to corroborate research questions.

According to Mata (2019) “The research approach is defined as the nature of the study, which manifests data collection as quantitative aspects and encompasses the research process in all its stages and interpretation of the data” (p. 1).

2.3. Paradigm

This research has an interpretative paradigm, because it is focused on the objective of the study, and qualitative techniques will be used. The objective of the research is the construction of practical theories.

According to Ayala (2021), “The interpretive paradigm in research is a model based on the understanding and description of what is being studied, which is a reaction to the explanatory and predictive concepts of the positivist paradigm”.

2.4. Data Collection

In this study, it was necessary to search for secondary information. We used magazines, books, and internet pages that provide information about integrals, vectors, fluid mechanics, miscible and non-miscible fluids, and prototypes, among others. Among others.

For Maranto and Gonzalez (2015) primary sources:

These types of sources contain original information, i.e. they are first-hand, and they are the result of ideas, concepts, theories, and research results. They contain direct information before being interpreted or evaluated by another person. The main sources of primary information are books, monographs, periodicals, official documents or technical reports from public or private institutions, theses, papers presented at conferences or seminars, expert testimonies, newspaper articles, video documentaries, and forums. (p.3).

2.5. Information Analysis

To analyze all the information collected, a series of coordinated processes have been carried out. Where the search for content regarding the subject under study is made, using an exploration aligned to documents, magazines, books, blogs, and websites, among others. The process is carried out step by step, where each content and source of information consulted is thoroughly analyzed and discussed among the collectors of the research process.

3. ANALYSIS OF RESULTS

It was possible to analyze sequentially and logically theoretical concepts of miscible fluids from vector calculus, where a great variety of information was found. However, very few of them have the necessary characteristics for referencing. Therefore, an attempt was made to take up only the necessary information supported and referenced.

Figure 1

Theoretical Foundations

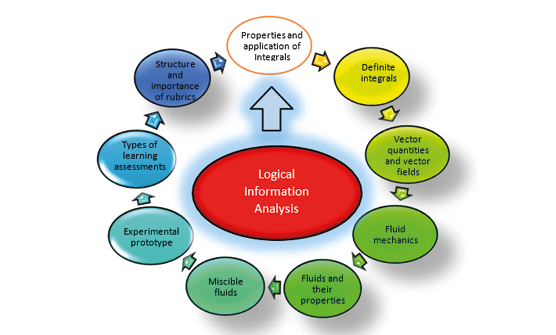
Note: Own creation based on the study of theoretical aspects.

It was possible to build a prototype of experimental practical work for the demonstration of stocks of miscible fluids from vector calculus. It is based on the following theoretical foundations:

Taking as a starting point Agüera (2011), who mentions that a fluid is a substance that deforms continuously and whose physical magnitudes define the state in which it is found. For example pressure, and temperature (common to all substances).

Iberti (2000) also states that “the main focus of miscible and non-miscible liquids is on the solubility of one liquid in another” (p. 2). Water and ethanol, for example, are miscible since they mix in all proportions. This implies that they would not be miscible if, in any proportion, they do not form a solution. For example, oil in water.

On the other hand, Coelho (2019) mentions that a vector is a line segment in space that starts from one point to another with direction and sense, thus expressing the so-called physical magnitudes.

We also start from De La Cruz (2019) who assures that the integral is an antiderivative, although they are complemented for the determination of areas under a curve, applying indefinite integrals in cases where it is required to calculate the area of two or more curves without definite values, also applying definite integrals to know the area of a specific section.

In addition, we have taken up Cuofano’s (2022) stipulation that a prototype is a sample version or simulation for evaluating a process or concept. Assuming that a prototype can be as simple as a storyboard sketch drawn on paper that captures the user experience or as detailed as a full-scale mock-up.

Based on the study background found in this research, several experiments with miscible fluids were carried out. Through this experimentation process, the miscibility of two or more fluids was known, as well as the non-miscibility in some cases, which is due to the difference in densities between the fluids.

The vectorial part in miscible fluids was analyzed from the molecular point of view. Knowing that the molecules are kept in constant motion in a disordered way, they move with a direction, sense, and velocity. Therefore, even being a random motion, each molecule could be related to a vector. Since, when mixing two or more miscible fluids, a vector field would be formed, where these molecular vectors move in all directions. However, it would not be possible to make a vector calculation as such, because they move unpredictably.

Miscible fluids are more common in our environment than non-miscible fluids. For this reason, it was decided to build a prototype to demonstrate the existence of miscible fluids from vector calculus. The prototype consists of a replica of a mock-up swimming pool, which reflects one of the possible applications in our daily life. To carry out the aforementioned demonstration, the following explanation found on YouTube was taken as a base idea, in which it is demonstrated how the integrals can be applied in the calculation of force in submerged plates caused by the pressure of a liquid. (LaMejorAsesoríaEducativa, 2019).

The following prototype was built, with the help of the materials:

Miscible fluids

• 1 sheet of plywood of 56 cm x 50 cm

• 1 sheet of plywood 50 cm x 35 cm

• 1 net 20 cm long by 10 cm wide.

• 1 Instant glue.

• 11 bamboo sticks. 4 of 26 cm long, 2 of 15 cm, 1 of 20 cm, and 4 of 4 cm long, all with a diameter of 1 cm.

• 1 plastic stick of 30 cm and ½ cm in diameter.

• 2 yards of 1/8” smooth wire.

• 1 watercolor.

• 4 plywood wheels of 12 cm diameter.

• 2 screws, 1 inch long.

• 1 transparent bucket 27 cm wide x 41 cm long x 24 cm high.

• Water and chlorine.

• 4 foamy sheets in red, purple, white, and pink.

• 1 light blue spray.

• 1 half-circumference-shaped plywood plate with a radius of 10 cm

• 4 clear plastic cups.

• Use of hot silicone trowel gun.

• 5 silicone rods.

• 1 small plastic ball.

• 2 pieces of tie wire.

Make the prototype through the following steps:

1. Two sheets of plywood are cut, one of 56 cm x 50 cm and the other of 50 cm x 35 cm.

2. Spray paint the two sheets of plywood, one on both sides and the other on one side only.

3. The upper part of the other plywood sheet is painted with watercolor.

4. The two sheets of plywood are glued with silicone and with the help of two one-inch long screws, one on the lower part of the tray and the other on the upper part.

5. The 4 bamboo sticks measuring 26 cm long are glued together with instant glue on the lower and upper corners of the plywood.

6. The frames of each chair are designed with 2-yard stranded wire.

7. Cut 4 sheets of plywood 4 cm wide by 8 cm long.

8. Next, we proceed to cover the 4 sheets of plywood with foamy.

9. After this, the 4 sheets of plywood are glued with silicone on the chair frames.

10. The plate is cut in the shape of a half-circumference with a radius of 10 cm.

11. The half-circular-shaped plywood plate was painted.

12. Glue the two bamboo sticks on each corner of the plate with instant glue and in the middle part of the plate we glue a bamboo stick with instant glue.

13. After this is done, glue the bottom part of the stick to the bucket.

14. The part of the two sticks that are glued to the top of the plate, on these two sticks we tie the volleyball net with nylon.

15. Next, we tie the plastic stick through the part where the plate is to hold it with a tie wire.

16. We cut 4 plywood wheels with 12 cm diameter.

17. The 4 plywood wheels were lined with foamy.

18. Next, glue the 4 sticks 4 cm long with the 4 plywood wheels.

19. After gluing the wheels with the sticks, they are glued with instant glue on the plywood sheet.

20. And finally, each edge of the bowl is lined with white foamy.

Figure 2

Steps for the construction of the Experimental Working Prototype

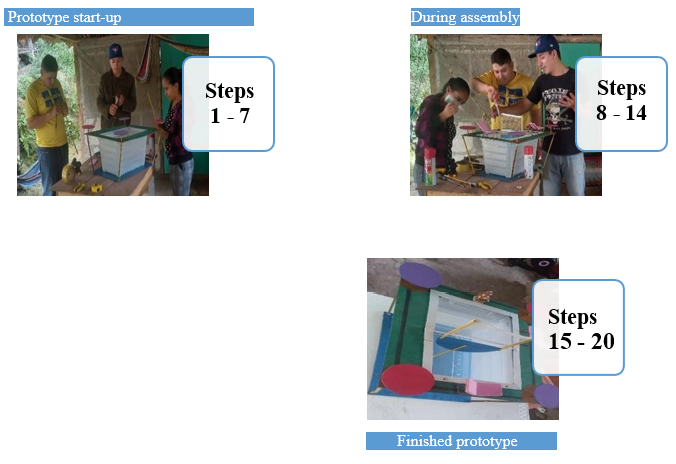
Note. Own creation from the creation of the own

Through the observation of the prototype shown in Figure 3, and supported by Figure 4, the following problem is posed, which serves as a complement in the demonstration: In a pool replicated on a small scale through a model, where the measures of the pool area; 27 cm wide x 41 cm long x 24 cm high. In it, there is a volleyball net, which is attached to a semicircular plate that serves as a base, with a radius of 10 cm. Therefore, it is required to calculate the force exerted by the fluid (which would be water and chlorine) on the plate.

Figure 3

Prototype

Note: Own creation, and construction of the prototype with easily accessible material.

Figure 4

Simulation of the sidewall parallel to the plate

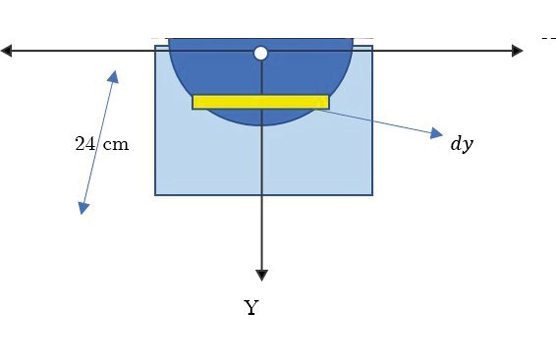
Note: Own creation

Data:

Height = 24 cm

Width = 27 cm

submerged plate radius = 10 cm

amount of submerged water = 24 liters

To start operations, the first step must be taken into account.

Step 1: Locate the reference system (coordinate axes) in Figure 8, so that the origin is at the center of the plate.

Step 2: Place a typical rectangle (dy) on the plate of Figure 8, which must be parallel to the water level, y of the x-axis is always located at a distance, this rectangle will move along the length and width of the plate when solving the integral.

Step 3: Clear the pressure equation to calculate the fluid force.

To find the force it is necessary to clear the force from the main equation.

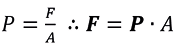
To know the pressure, the following formula is applied.

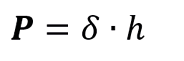
Once the clearance is done, we are left with the fact that the force is equal to the pressure times the area, but in this case, instead of p, it will be located at :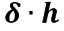

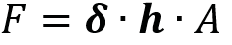
Important data:

This leaves us with only one formula to find the force. Substituting pressure and area for their equality.

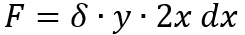
Step 4: Analyze the equation of the circumference as a function of Figure 8, to work the plate.

In this case, the center would be (0,0). Therefore c(ℎ, k) = (0,0). (x − ℎ)2 + (y − k)2 = R2

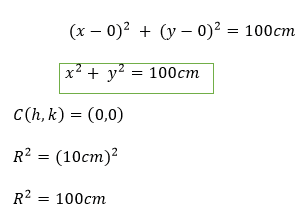
Step 5: With the analyzed data, the general equation of the circumference adapted to the submerged plate can be worked out. Therefore, we must determine “x” as a function of “y”. Replacing the values we develop the equation to find the value of “x”.

x2 + y2 = 100cm

x2 = 100 cm − y2

x = √100 − y2

𝑥 = 10 − 𝑦

Step 6: Propose the integral that allows us to obtain the force.

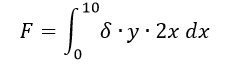
At this point, we replace the “x” value to obtain a more specific equation.

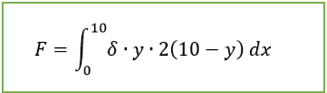
By analyzing the problem posed above, it was possible to demonstrate the existence of miscible fluids, which would be the mixture of water and chlorine poured into the pool. Similarly, there is a submerged plate that serves as the base of the volleyball net, then using the definite integrals and some physics formulas, it was possible to demonstrate the calculation of the force exerted by the fluid on the plate.

Finally, the most significant results are:

For miscibility to exist, both fluids must share the same density.

In a miscible fluid, the vectorial part can be visualized from the molecular point of view, where each molecule would be a vector since it moves with a sense, direction, and at speed. Although it would not be possible to do vectorial calculations as such because they move in all directions randomly.

Using fluid mechanics equations, geometry, and definite integrals, it is possible to calculate the force exerted by the fluid on the submerged plate shown in Figures 2 and 3.

In addition, the great importance of miscible fluids in our daily life was learned.

Among the factors or influential variables that can affect the results would be the lack of knowledge of the meaning of what a fluid is, since there is a wide range of chemicals that give rise to solubility, but these are not considered fluids. For example, sugar with water, both mix, but sugar in its natural state is a solid, therefore, it does not belong to the fluids.

Among the strengths is the collaborative work among the research group, communication, common interest in reaching a good conclusion, and excellent results. The limitations of the study include not having more than one computer, which slows down the research process, and the poor quality of the internet signal has been one of the main obstacles.

Concerning the findings found through this study, we have investigated intending to find scientific support for the results found, but no similar publication has been discovered. Therefore, the possibility is left open for future researchers to give continuity to the present investigation, or to improve the findings. Likewise, a search was made for arguments or publications that indicate the opposite of the results obtained in the present work. However, nothing related was found.

Taking into account the factors that could have influenced these results. One can mention the use of more common and easily accessible fluids used for experimentation. Another factor would be the combination with vector calculus plus the relationship involving algebra, integrals, fluid mechanics, and forms of evaluation.

As for the meaning of the present work carried out. It is oriented to the construction of an experimental practical prototype, to be able to reflect the existence of miscible fluids from the vectorial calculation. Where a demonstration will be given utilizing the prototype of experimental practical work already mentioned before.

The importance of this research goes beyond a demonstration since important aspects of the results obtained can be taken up again to strengthen future research, or to give continuity to it. It can also be a fundamental basis for developing content involved in the theoretical foundation and reflected in the demonstration. On the other hand, it can give rise to new ideas of scientific utility.

When you decide to undertake a research process is because you want to know results, starting from the questions that do not satisfy the knowledge gap, therefore, for this study to achieve the expected satisfaction is necessary to perform all the procedures involved in such research already mentioned above, so it is in this way how you get to know, analyze, interpret, experiment, discuss based on the results to reach a single conclusion.

Among the implications of the research we have:

•To verify what was stated in the objectives of the study.

•Examine the results obtained from the whole process.

•To take into account the lines of research that are the applications of the exact sciences, applied mathematics, and applied physics.

For the evaluation of the research work carried out, an evaluation rubric was elaborated in which it will be possible to grade from 0 to 100%. In the same way, the quality of the work done will be taken into account. That is to say, for the study to reach 100% qualification, it must have a good presentation, coherence, logic, and sense, as well as the requirements to be considered a scientific study. Therefore, it must comply with the predetermined research standards.

The heading is as follows:

Table 1

Research Paper Evaluation Rubric

Note: Own creation

4. CONCLUSIONS

Through the investigation and analysis of theoretical concepts, starting with integrals, it was discovered that the direct relationship with miscible fluids is not so common in real situations. The same happens with the vectorial part since such vector applications are more oriented to other situations. Even so, the part of fluid mechanics was analyzed where a great relationship is found since this branch is in charge of studying the motion of fluids. Miscibility was also studied, which has been of fundamental importance for the whole research process since these are very common in our environment. Also, the concepts of prototypes were studied which have been very important to establish an effective demonstration of the subject under study.

Once the theoretical support was obtained, we were able to build a prototype embodied in an experimental model alluding to a possible situation in our daily life. This was made with very common materials in our environment and easy access. Once the construction was finished, the experimentation process was carried out, where it was possible to demonstrate the existence of miscible fluids from the vectorial calculation.

However, it is important to mention that a previous analysis of miscible fluids was carried out through experimentation, leaving evidence of the existence of such fluids. However, it has been shown that miscibility between fluids is more common than non- miscibility, this is due to the following; Whenever two or more fluids share the same density, miscibility will occur.

For the evaluation of this study in general, a structured rubric was elaborated according to the pre-established standards, through which the research work can be qualified, and thus be able to identify aspects to be improved in subsequent research. In addition to guiding the process of studies that require evaluation.

Using the rubric, it was possible to evaluate important evaluation criteria that imply the quality of the document, compliance with research standards, such as objectivity and scientificity of the study, in addition to coherence in all aspects of the process. As well as the interdisciplinarity in the work done by linking other branches of study such as Algebra, Calculus, Structure of Matter, and Educational Evaluation.

Glossary of technical or specialized terms