Introducción

Pruebas de hipótesis

El establecimiento y la comprobación de hipótesis es una parte esencial de los estudios estadísticos. Para formular una prueba de este tipo, normalmente se propone una teoría, la cual aún no se ha demostrado que sea cierta. Por ejemplo, supongamos que se ha afirmado de que un nuevo fármaco para ayudar a combatir la infección funciona mejor que el actual. Queremos establecer y probar una hipótesis para determinar si esta afirmación es cierta.

Las pruebas de hipótesis siempre comienzan con una afirmación sobre un parámetro de la población. En general, cuando se discuten las hipótesis se consideran dos afirmaciones que son directamente contradictorias entre sí. El proceso de comprobación de las hipótesis nos proporciona argumentos de por qué una determinada hipótesis puede ser aceptada o rechazada.

La hipótesis planteada se llama hipótesis nula y la denotamos por H₀ y la hipótesis alternativa afirma lo contrario y se denota por H₁.

Consideremos un ejemplo sobre unos pollos de engorde. Supongamos que los datos de años anteriores indican que el peso medio de la población de pollos de engorde es de 2 kg. Queremos estimar el peso medio de los pollos de engorde de este año, y para ello tomamos una muestra de cierto tamaño. La media de la muestra es de 2,0 kg. La hipótesis nula siempre afirma que no hay cambios, es decir, que el peso medio de los pollos de engorde este año es también de 2 kg. Lo escribimos como $H_0:\mathrm{\mu }=\bar{x}$ (donde $\mu$ es la media poblacional y $\bar{x}$ es la media muestral.)

La hipótesis alternativa puede tener diferentes enunciados en función del tipo de prueba que queramos realizar.

Hay dos tipos de pruebas de hipótesis y tres tipos de hipótesis alternativas

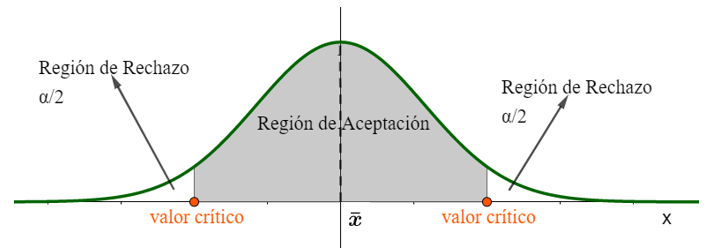
i. Prueba de dos colas $(H_1:\mathrm{\mu }\ne \bar{x})$ : en el ejemplo significa que el peso medio de los pollos es diferente de 2 kg.

Figura 1.
Prueba de hipótesis de dos colas

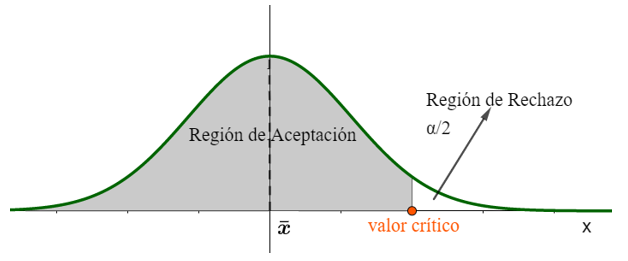
ii. Prueba de una cola superior $(H_1:\mathrm{\mu }>\bar{x})$ : el peso medio de los pollos es mayor a 2 kg.

Figura 2.
Pruebas de hipótesis de una cola superior

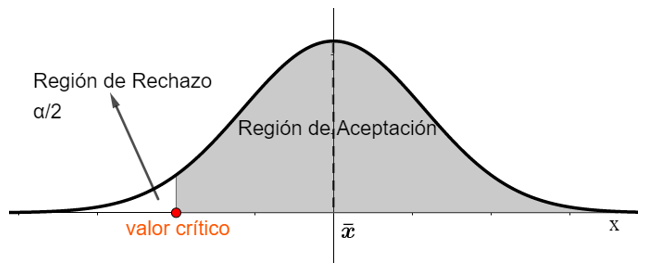
iii. Prueba de una cola inferior $(H_1:\mathrm{\mu }<\bar{x})$ : el peso medio de los pollos es menor a 2 kg.

Figura 3.
Prueba de hipótesis de una cola inferior

También debemos decidir qué nivel de significación, α, necesitamos para concluir que una determinada hipótesis es aceptada, con $(1-\alpha )\%$ de certeza. El nivel de significación está directamente relacionado con el intervalo de confianza, por lo que si estamos seguros al 95% de que el valor medio está en el intervalo de confianza podemos aceptar la hipótesis nula con un nivel de significación del 5% de la prueba.

Los niveles de significancia usualmente son 1%, 5% y 10%. Al calcular los estadísticos de prueba, al igual que calcular los intervalos de confianza, se utiliza los estadísticos z sino el estadístico -t. Utilizaremos el estadístico -z cuando la varianza sea conocida, y el estadístico -t cuando la varianza es desconocida (independientemente del tamaño de la muestra, en este estudio no hace relevancia a este último).

Hay dos maneras de tomar una decisión basada en los valores calculados.

• El valor crítico es el valor z o el valor t encontrado en el nivel de significación de la prueba. Si el valor z o t de la prueba se encuentra fuera de la llamada región de aceptación, rechazamos la hipótesis nula, en caso contrario, no la rechazamos.

• El valor p es la probabilidad de que el parámetro que investigamos (es decir, la media) se encuentre dentro de la región de rechazo, dado que la hipótesis nula es verdadera. Si el valor p es mayor que el nivel de significación no podemos decir que aceptamos la hipótesis nula, sino que decimos que "no tenemos pruebas suficientes para rechazar", o simplemente "no rechazamos", la hipótesis nula.

Tenemos cuatro pasos a seguir en una prueba de hipótesis

1. Paso 1. Establecer la hipótesis nula y alternativa

2. Paso 2. Establecer un criterio para una decisión

3. Paso 3. Calcular los estadísticos necesarios

4. Paso 4. Decidir o tomar una decisión en base a los estadísticos calculados y criterios de decisión.

Nivel de significancia

El nivel de significación es el límite para juzgar un resultado como estadísticamente significativo. Si el valor de significación es menor que el nivel de significación, se considera que el resultado es estadísticamente significativo. El nivel de significación también se conoce como el nivel alfa. (Cognos Analytics, 2021)

Pruebas de hipótesis para cuando la media y la desviación es conocida

Como en el cálculo de los intervalos de confianza, utilizamos z-estadístico en pruebas de hipótesis. Vamos a ver un ejemplo en el cual lo relacionaremos con el intervalo de confianza.

A continuación, se presentará un par de ejemplos en la parte de desarrollo, con los métodos que indican las bibliografías, en los cuales se aborda el análisis y conclusión de la misma.

Desarrollo

EJEMPLO 1

Se sabe que el tiempo de secado de un tipo de pintura para coches tiene una distribución normal con una media de 75 minutos y una desviación estándar de 9 minutos. Los pintores de coches de una empresa automovilística han descubierto un aditivo que acorta el tiempo de secado. Sin embargo, si la empresa aprueba el uso de este aditivo, el coste de pintar un coche aumentará naturalmente. No lo aprobarán a menos que tengan pruebas sólidas de que el aditivo reduce el tiempo de secado. Una prueba en 49 coches nuevos dio un tiempo medio de secado de 72 minutos^[a].

Usando un nivel de significancia del 5%, ¿Qué le recomendarías a la empresa?

Solución

Establecemos las hipótesis nula y afirmativa

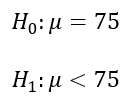
Utilizando la calculadora Texas Instrument, obtenemos los siguientes resultados:

Realizando las comparaciones del valor - p probabilístico con en el nivel de significancia $\mathrm{\alpha }$

0.0098<0.05

Como este valor es inferior al 5%, rechazamos la hipótesis nula y concluimos que tenemos pruebas suficientes de que el tiempo medio de secado es inferior a 75 minutos. Por lo tanto, la empresa puede seguir adelante y empezar a utilizar el aditivo.

EJEMPLO 2

En cierto país se cree que la altura media de la población de hombres es 182 cm y la desviación estándar de 5 cm. Una muestra aleatoria de 100 hombres fue tomada de la población y la altura media encontrada fue de 183.6 cm.^[b]

• Establezca la hipótesis nula y alternativa

• Use una prueba de dos colas con un nivel de significancia del 10% para decidir si la afirmación es verdadera o no.

Solución A

Nuestra hipótesis nula H₀ es mantener la afirmación de que la media poblacional ($\mathrm{\mu }$) es de 182 cm expresándose de la siguiente manera:

$H_0:\mathrm{\mu }=182$

La hipótesis alternativa plantea lo contrario a la hipótesis nula, en este caso como se pide una prueba de dos colas se establece como:

$H_1:\mathrm{\mu }\ne 182$

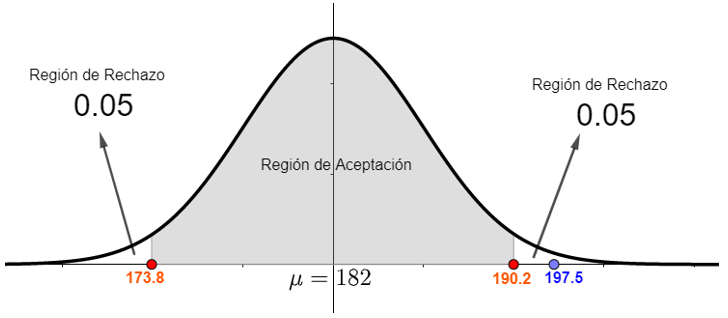
Gráficamente con un nivel de significación del 10% esto quiere decir lo siguiente

Figura 4.
Representación de la información del problema brindado

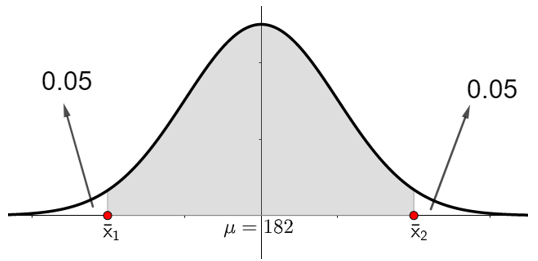
Realizando una estandarización para z donde $z_1\equiv x_1$ y $z_2\equiv x_2$ tenemos lo siguiente:

La desviación estándar muestral se calcula de la siguiente manera

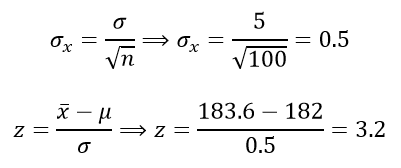
Dado que $\mathrm{\alpha }=0.1$, es la región de rechazo repartida en las dos colas,

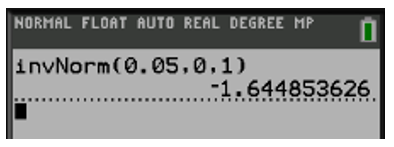
El valor de estandarizado de $z_1~z_{\alpha /2}$ para un área de 0.05 es

Por su simetría $z_1=1.645$ , se procede a comparar z y z₁ , resultando respectivamente la comparación 3.2>1.645, gráficamente lo podemos ver así

Figura 5.
Información en una curva normal estandarizada

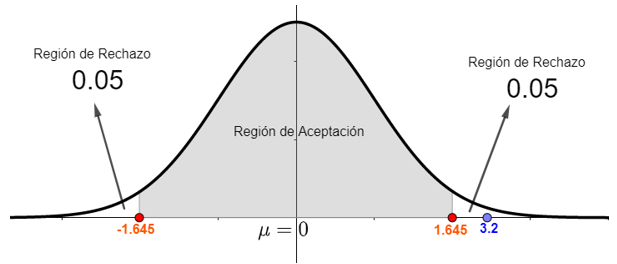
El valor de z=3.2 que es la estandarización de 197.5 queda fuera de la región de aceptación por lo que la hipótesis nula se rechaza a un nivel de significancia del 10%.

Esta conclusión podemos hacerla extensiva a los intervalos de confianza. En el ejemplo anterior al regresar la estandarización a la variable aleatoria X se observa así

Figura 6.
Información de resultados para la curva no estandarizada

Realizando el cálculo de intervalos de confianza en esta situación aplicando el uso de la calculadora estadística obtenemos la siguiente información.

Figura 7.
Resultados brindados por la Texas instruments calculator

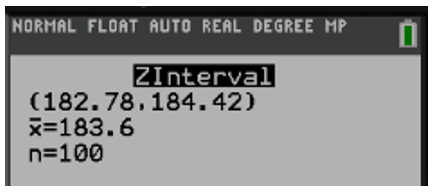
El intervalo de confianza nos confirma una vez más que la hipótesis nula establecida se debe rechazar dado que lo que se cree como media poblacional ($\mathrm{\mu }=182$) está fuera del intervalo de confianza (182.78,184.42).

Es sabido que en un intervalo de confianza entre más grande sea el tamaño de la muestra más inferencia precisa se realizará sobre la media poblacional de una variable aleatoria que se estudia, como por ejemplo, se realiza una encuesta en un determinado país, entre más personas integremos a la encuesta más preciso será el valor de la media muestral de una variable aleatoria en estudio hacia la media de toda la población de esa variable aleatoria

Se procede a revisar el siguiente ejemplo número tres.

EJEMPLO 3

Cuando comparamos el valor p con cada uno de los niveles de significación comunes (1%, 5% y 10%), concluimos que rechazamos la hipótesis nula en los tres niveles de significación, ya que 0,0037 es menor que todos y cada uno de ellos.

Después de una noche de lluvia, 12 lombrices han salido a la superficie en la tierra. Sus longitudes, medidas en cm, eran las siguientes: 12.0, 11.1, 10.5, 10.8, 12.1, 10.4, 10.9, 12.2, 10.9, 11.9, 11.12, 11.6. Se sabe que las lombrices proceden de una población que sigue una distribución normal con el valor promedio de 10,5 cm y una desviación estándar de 2 cm. Se cree que las lombrices están aumentando de tamaño^[c].

• Indique las hipótesis nula y alternativa

• Utilice una prueba superior de una cola al nivel de significación del 5% para decidir si la afirmación es verdadera o no.

Solución

$H_0:\mathrm{\mu }=10.5$

$H_1:\mathrm{\mu }>10.5$ es la creencia de que las lombrices están aumentando en su tamaño

Solución B

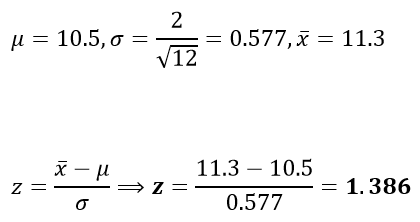
El valor de z critico dado que es en una cola tiene como valor $\alpha =0.05\to z_{\alpha }=z_{0.95}=1.645$

Comparando $z_{\alpha }>z$ , 1.645>1.386 con esto se concluye que no tenemos suficiente evidencia para rechazar la hipótesis nula con un nivel de significancia del 5%.

Revisando el problema por el método de p, obtenemos utilizando la calculadora estadística, Texas instrument

Figura 8.
Comparación de resultados con la Texas instruments calculator

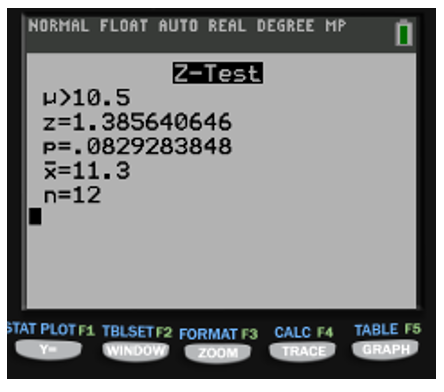
Realizando la comparación de p y $\alpha$, resulta 0.0829>0.05, podemos concluir en el problema que no tenemos suficiente evidencia para rechazar la hipótesis.

El ejemplo finaliza hasta aquí.

¡Pero analicemos un poco más a fondo el asunto!

Ahora agreguemos a este ejemplo anterior un tercer inciso con el siguiente enunciado

c. Ahora utilice un nivel de significancia del 10% y realice nuevamente las comparaciones y criterio de conclusión

Para darle solución, al efectuar las comparaciones resulta tener: 0.0829<0.10, en este caso cambia la conclusión a rechazar la hipótesis nula, y así se mantiene para todos los casos donde el nivel de significancia es mayor al 10%.

Conclusiones

Mantener un nivel significancia Alpha entre el rango de 1%-9% es completamente poco óptimo para la inferencia de un parámetro como la media muestral hacia la media poblacional. En el ejemplo 2 del desarrollo podemos observar que si cambiamos el nivel de significancia a un $\alpha =10\%$, la conclusión en el problema cambia a rechazar rotundamente la hipótesis nula y esta decisión se mantendría para cualquier nivel de significancia mayor a 10%. Esto podemos interpretarlo como si tuviéramos un abanico amplio de opciones para inferir en la media poblacional y cualquiera que sea la propuesta sería aceptada, mientras que un nivel de significancia no tan pequeño defínase mayor al 10% reduce esas múltiples opciones a un abanico más pequeño donde podemos inferir de manera más precisa o cercana a la media poblacional. Podemos también verlo con este ejemplo: si te digo que pienso en un número del 1 al 1000 y que me digas cuál es ese número, tu respuesta quizás sería poco asertiva para inferir en el número que pienso, mientras, que si te digo que pienso en un número entre 1al 5 tu respuesta estaría más cerca o exactamente das con el número que tengo en mente.

En base al artículo de la doctora Cabana, donde expresa: “que estos valores de significancia no pueden ser ni arbitrarios ni convenidos. Aunque en la comunidad científica por lo general en muchos campos se utiliza el valor estándar, posiblemente porque es un tema aun a día hoy debatido…” (Cabana, 2021) Es por eso por lo que no podemos mantener la teoría de que el nivel de significancia debe estar entre 1% y 10%, al contrario, si se desea inferir fielmente a la media poblacional debemos elegir un nivel de significancia mayor o igual al 10% y no quedarnos con esos valores de nivel de significancia muy bajos.

El tener un nivel de significancia muy pequeño más bien genera mucha confianza, lo cual en este tipo de situaciones no sería correcto ser muy confiados, pues aceptaríamos cualquier propuesta que se brinde por ser demasiado confiados.

Se abre el debate, propuestas y análisis para las personas que revisen este documento.

Referencias

Cabana, E. (octubre de 2021). Aprende con Eli. Porqué el nivel de significación es 0..05?: https://aprendeconeli.com/por-que-nivel-significacion-005/

Cognos Analytics. (31 de agosto de 2021). IBM Cognos Analytics.https://www.ibm.com/docs/es/cognos-analytics/11.1.0?topic=terms-significance-level

Harcet, J., Heinrichs, L., Seiler, P. M., & Torres Skoumal, M. (2014). Mathematics Higher Level, STATISTICS. Great Britain: Oxford University Press.

Quinn, C., Blythe, P., Haese, R., & Haese, M. (2013). Mathematics for the International Students Mathematics HL (Option) Statistics and Probability. Australia: Haese & Harris Publications 2013.

Notas